Квадратное уравнение

Квадратным уравнением называется уравнение ax²+bx+c=0, где a, b, c – заданные числа, a≠0, x -неизвестное.
Коэффициенты a, b, c квадратного уравнения обычно называют так: a – первым или старшим коэффициентом, b – вторым коэффициентом, c – свободным членом.
Например, в уравнении 3х²-х+2=0 старший (первый) коэффициент а=3, второй коэффициент b=-1, а свободный член c=2.
Решение многих задач математики, физики, техники сводится к решению квадратных уравнений:
2x²+x-1=0, x²-25=0, 4x²=0, 5t²-10t+3=0.
При решении многих задач получаются уравнения, которые с помощью алгебраических преобразований сводятся к квадратным. Например, уравнение 2x²+3x=x²+2x+2 после перенесения всех его членов в левую часть и приведения подобных членов сводится к квадратному уравнению x²+x-2=0.

Рассмотрим уравнение общего вида: ax²+bx+c=0, где a≠0.
Корни уравнения находят по формуле:
Выражение
называют дискриминантом квадратного уравнения.
Если D<0, то уравнение не имеет действительных корней; если D=0, то уравнение имеет один действительный корень; если D>0, то уравнение имеет два действительных корня.
В случае, когда D=0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.

Неполные квадратные уравнения. Если в квадратном уравнении ax²+bx+c=0 второй коэффициент b или свободный член c равны нулю, то квадратное уравнение называется неполным.
Неполное квадратное уравнение может иметь один из следующих видов:
Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения - проще решить уравнение методом разложения его левой части на множители.

Квадратное уравнение вида x2+px+q=0 называется приведенным. В этом уравнении старший коэффициент равен единице: a=1.
Корни приведенного квадратного уравнения находятся по формуле:
Этой формулой удобно пользоваться, когда p – четное число.
Пример: Решить уравнение x2-14x-15=0. По формуле находим:
Ответ: x1=15, x2=-1.

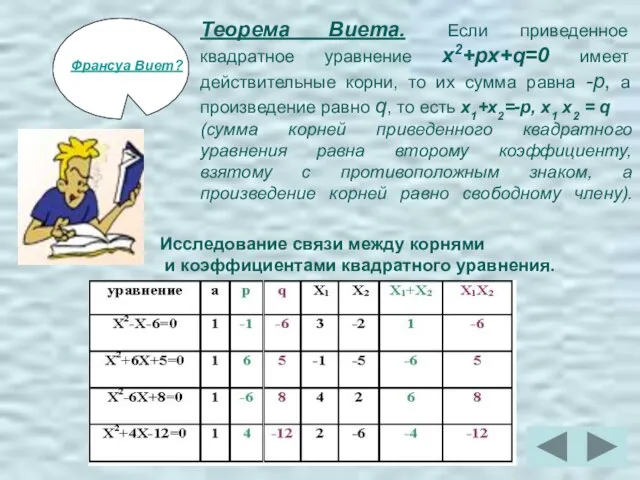
Франсуа Виет?
Теорема Виета. Если приведенное квадратное уравнение x2+px+q=0 имеет действительные корни, то их сумма равна -p, а произведение равно q, то есть x1+x2=-p, x1 x2 = q
(сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).
Исследование связи между корнями
и коэффициентами квадратного уравнения.

Утверждение №1:
Пусть х1 и х2 – корни уравнения
х2+pх+q=0.
Тогда числа х1, х2 , p, q связаны равенствами:
x1 +х2 = - p, х1 х2 =q
Утверждение № 2:
Пусть числа х1, х2, p, q связаны равенствами х1+х2 = - p, х1 х2 =q.
Тогда х1 и х2 – корни уравнения
х2+pх+q=0
Следствие: х2+pх+q=(х-х1 )(х-х2).
Ситуации, в которых может использоваться теорема Виета.
Проверка правильности найденных корней.
Определение знаков корней квадратного уравнения.
Устное нахождение целых корней приведенного квадратного
уравнения.
Составление квадратных уравнений с заданными корнями.
Разложение квадратного трехчлена на множители.

Биквадратные уравнения
Биквадратным называется уравнение вида , где a≠0. Биквадратное уравнение решается методом введения новой переменной: положив , получим квадратное уравнение
Пример: Решить уравнение
x4+4x2-21=0
Положив x2=t, получим квадратное уравнение t2+4t -21=0, откуда находим t1= -7, t2=3. Теперь задача сводится к решению уравнений x2= -7, x2=3.
Первое уравнение не имеет действительных корней, из второго находим:
которые являются корнями заданного биквадратного уравнения.

Решение задач с помощью квадратных уравнений
Задача 1:
Автобус отправился от автовокзала в аэропорт, находящийся на расстоянии 40 км. Через 10 минут вслед за автобусом выехал пассажир на такси. Скорость такси на 20 км/ч больше скорости автобуса. Найти скорость такси и автобуса, если в аэропорт они прибыли одновременно.
На 10 мин
10 мин =
ч
Составим и решим уравнение:

Умножим обе части уравнения на 6x(x+20), получим:
Корни этого уравнения:
При этих значениях x знаменатели дробей, входящих в уравнение, не равны 0, поэтому являются корнями уравнения. Так как скорость автобуса положительна, то условию задачи удовлетворяет только один корень: x=60. Поэтому скорость такси 80 км/ч.
Ответ: Скорость автобуса 60 км/ч, скорость такси 80 км/ч.

Задача 2:
На перепечатку рукописи первая машинистка тратит на 3 ч меньше, чем вторая. Работая одновременно, они закончили перепечатку всей рукописи за 6ч 40 мин. Сколько времени потребовалось бы каждой из них на перепечатку всей рукописи?
Вместе
за 6ч 40мин
6 ч 40 мин = 6 ч
Составим и решим уравнение:

Это уравнение можно записать следующим образом:
Умножая обе части уравнения на 20x(x+3), получаем:
Корни этого уравнения:
При этих значениях x знаменатели дробей, входящих в
уравнение, не равны 0, поэтому - корни
уравнения. Так как время положительно, то x=12ч. Следовательно
Первая машинистка затрачивает на работу 12 ч, вторая – 12 ч + 3 ч = 15 ч
Ответ:12 ч и 15 ч.

Задания для самостоятельной работы:
7.Найти два последовательных натуральных
числа, произведение которых равно 210.

Желаем удачи!!!