Преобразования графиков функций. Алгебра и начала анализа, 10 класс.

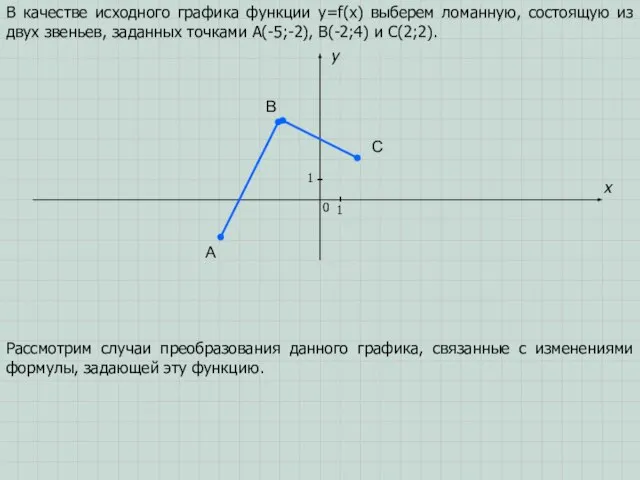
A
B
C
x
y
0
1
1
В качестве исходного графика функции y=f(x) выберем ломанную, состоящую из двух звеньев, заданных точками A(-5;-2), B(-2;4) и C(2;2).
Рассмотрим случаи преобразования данного графика, связанные с изменениями формулы, задающей эту функцию.

A
B
C
x
y
I. y=f(x)+a, где a∈.
1
1
0
В новой формуле значения функции (ординаты точек графика) изменяются на число a, по сравнению со «старым» значением функции. Это приводит к параллельному переносу графика функции вдоль оси Oy:
вверх на a ед.отр., если a>0 или
вниз на a ед.отр., если a<0.
Например:
1) y=f(x)+3;
A1
B1
C1
y=f(x)
y=f(x)+3
или 2) y=f(x)–2.
A2
B2
C2
y=f(x)-2

A
B
C
x
y
I. y=f(x)+a, где a∈.
1
1
0
Понятие «параллельного переноса вдоль оси Oy вверх…, вниз…» можно заменить на «параллельный перенос на вектор с координатами ».
A1
B1
C1
y=f(x)
y=f(x)+3
A2
B2
C2
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
y=f(x)-2

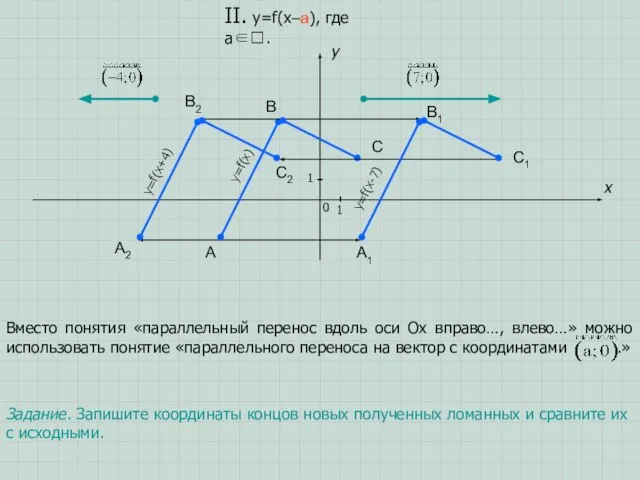
A
B
C
x
y
0
1
1
II. y=f(x–a), где a∈.
В новой формуле значения аргумента (абсциссы точек графика) изменяются на число a, по сравнению со «старым» значением аргумента. Это приводит к параллельному переносу графика функции вдоль оси Ox:
вправо на a ед.отр., если a>0 или
влево на a ед.отр., если a<0.
Например:
1) y=f(x–7)
y=f(x)
y=f(x-7)
A1
B1
C1
или 2) y=f(x–(–4))=f(x+4).
A2
B2
C2
y=f(x+4)

A
B
C
x
y
0
1
1
II. y=f(x–a), где a∈.
Вместо понятия «параллельный перенос вдоль оси Oх вправо…, влево…» можно использовать понятие «параллельного переноса на вектор с координатами .»
y=f(x)
y=f(x-7)
A1
B1
C1
A2
B2
C2
y=f(x+4)
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.

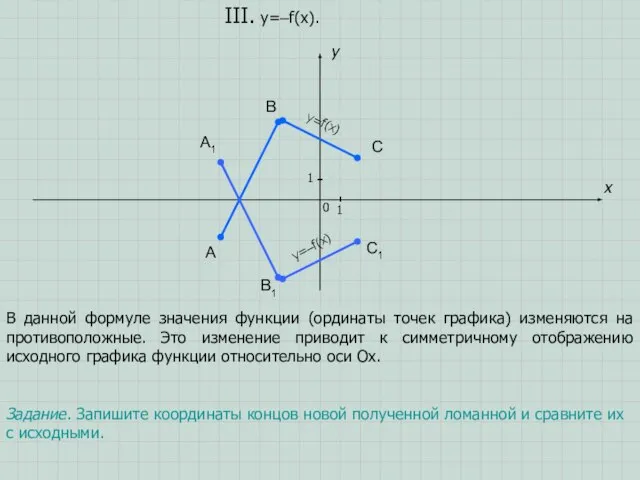
A
B
C
x
y
III. y=–f(x).
0
1
1
A1
B1
C1
В данной формуле значения функции (ординаты точек графика) изменяются на противоположные. Это изменение приводит к симметричному отображению исходного графика функции относительно оси Ох.
Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными.
y=f(x)
y=–f(x)

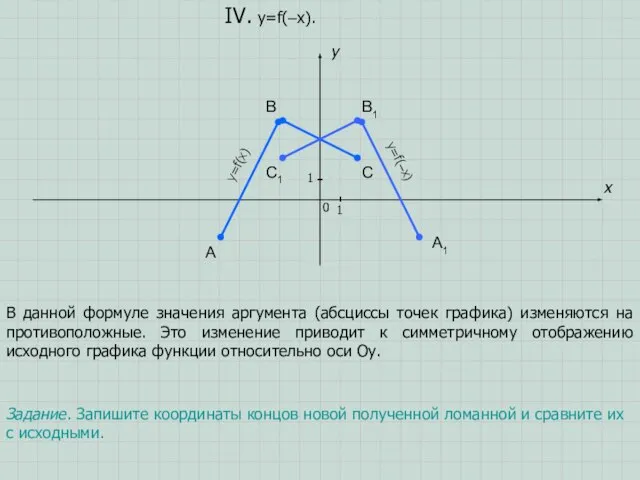
A
B
C
x
y
0
1
1
IV. y=f(–x).
В данной формуле значения аргумента (абсциссы точек графика) изменяются на противоположные. Это изменение приводит к симметричному отображению исходного графика функции относительно оси Оу.
A1
B1
C1
Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными.
y=f(x)
y=f(–x)

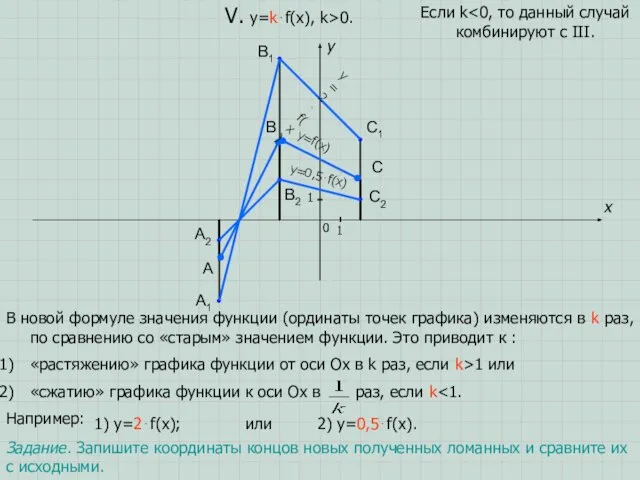
A
B
C
x
y
0
1
1
V. y=k⋅f(x), k>0.
В новой формуле значения функции (ординаты точек графика) изменяются в k раз, по сравнению со «старым» значением функции. Это приводит к :
«растяжению» графика функции от оси Oх в k раз, если k>1 или
«сжатию» графика функции к оси Ох в раз, если k<1.
Например:
1) y=2⋅f(x);
или 2) y=0,5⋅f(x).
A1
B1
C1
y=f(x)
y=2⋅f(x)
A2
B2
C2
y=0,5⋅f(x)
Если k<0, то данный случай комбинируют с III.
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.

A
B
C
x
y
0
1
1
VI. y=f(k⋅x), k>0.
В новой формуле значения аргумента (абсциссы точек графика) изменяются в k раз, по сравнению со «старым» значением аргумента. Это приводит к :
1) «растяжению» графика функции от оси Oу в раз, если k<1 или
2) «сжатию» графика функции к оси Оу в k раз, если k>1.
Например:
Если k<0, то данный случай комбинируют с IV.
1) y=f(0,5⋅x);
или 2) y=f(2⋅x).
Задание. Запишите координаты концов новых полученных ломанных и сравните их с исходными.
A1
B1
C1
A2
B2
C2
y=f(x)
y=f (0,5⋅x)
y=f(2⋅x)

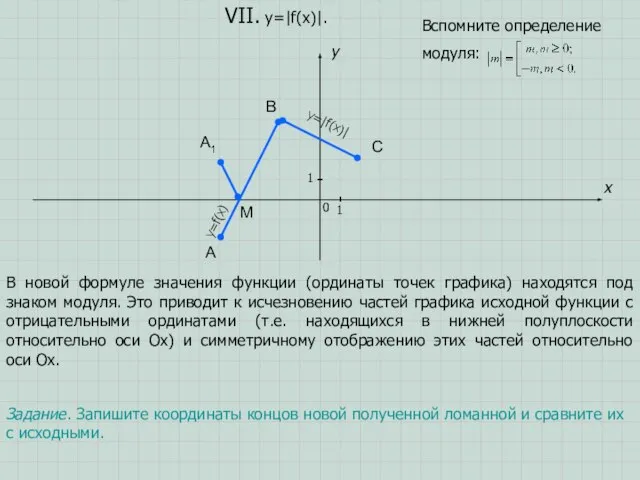
A
B
C
x
y
0
1
1
VII. y=|f(x)|.
Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными.
В новой формуле значения функции (ординаты точек графика) находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными ординатами (т.е. находящихся в нижней полуплоскости относительно оси Ох) и симметричному отображению этих частей относительно оси Ох.
A1
M
Вспомните определение
модуля:
y=f(x)
y=|f(x)|

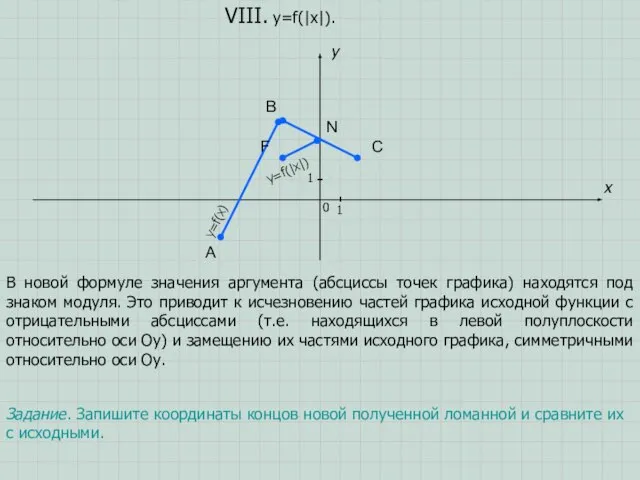
A
B
C
x
y
0
1
1
VIII. y=f(|x|).
Задание. Запишите координаты концов новой полученной ломанной и сравните их с исходными.
В новой формуле значения аргумента (абсциссы точек графика) находятся под знаком модуля. Это приводит к исчезновению частей графика исходной функции с отрицательными абсциссами (т.е. находящихся в левой полуплоскости относительно оси Оу) и замещению их частями исходного графика, симметричными относительно оси Оу.
N
F
y=f(x)
y=f(|x|)

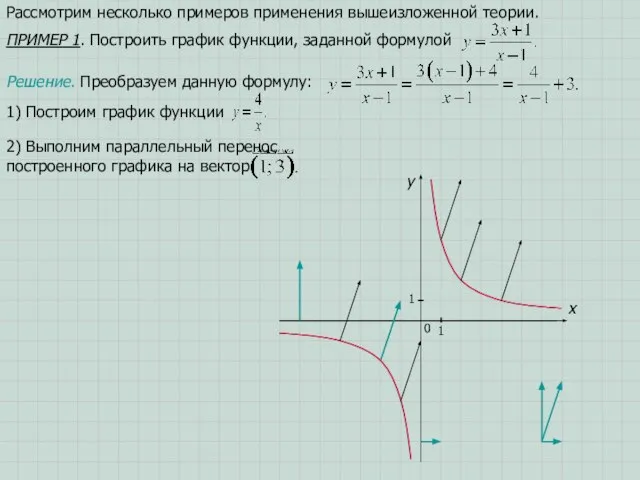
x
0
1
1
y
Рассмотрим несколько примеров применения вышеизложенной теории.
ПРИМЕР 1. Построить график функции, заданной формулой

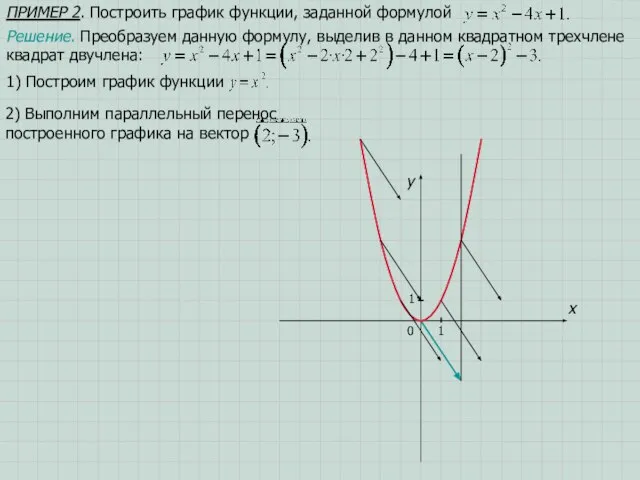
ПРИМЕР 2. Построить график функции, заданной формулой
x
1
y
0
1

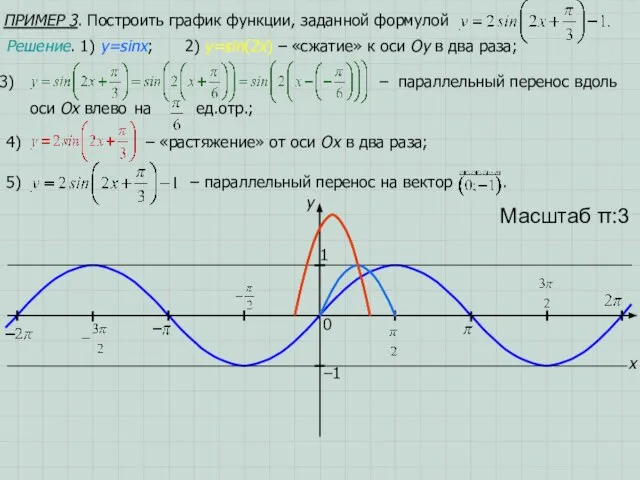
ПРИМЕР 3. Построить график функции, заданной формулой
x
y
1
0
Масштаб π:3
−1
Решение. 1) y=sinx;
2) y=sin(2x) – «сжатие» к оси Оу в два раза;