Слайд 2 Графики и свойства тригонометрических функций синуса и косинуса
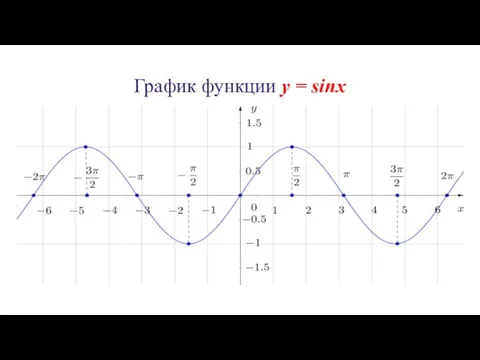
График функции y

= sinx
Свойства функции y = sinx
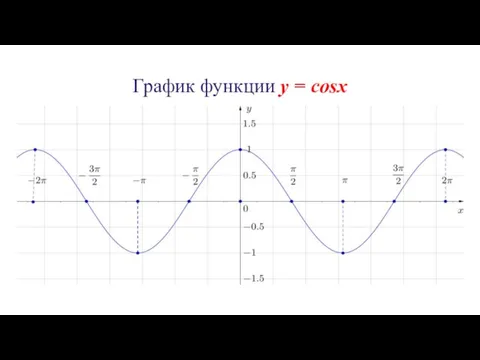
График функции y = cosx
Свойства функции y = cosx
Сравнение свойств функций y = sinx и y = cosx
Слайд 3Тригонометрический круг и числовая прямая
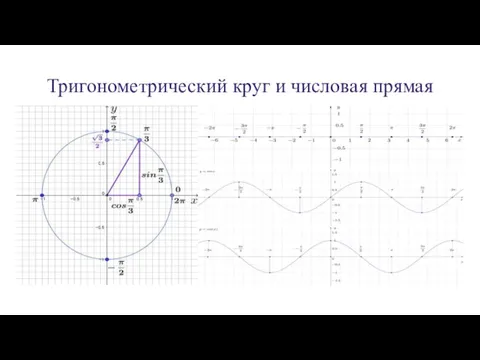
Слайд 4Тригонометрический круг и числовая прямая
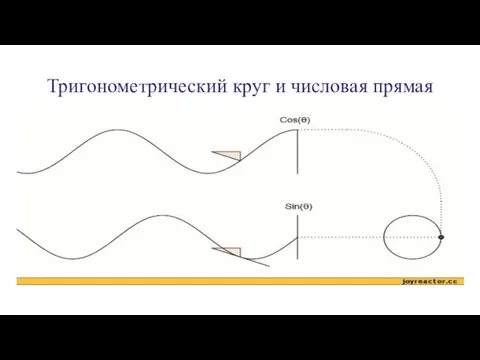
Слайд 6Свойства функции y = sinx
1. Область определения функции y = sinx: D(sinx)
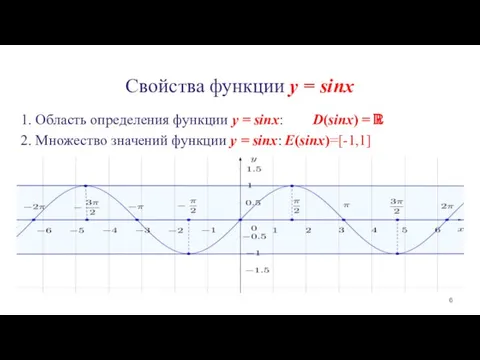
= ℝ
2. Множество значений функции y = sinx: E(sinx)=[-1,1]
Слайд 7Свойства функции y = sinx
3. Функция y = sinx нечетная: sin(–x) =
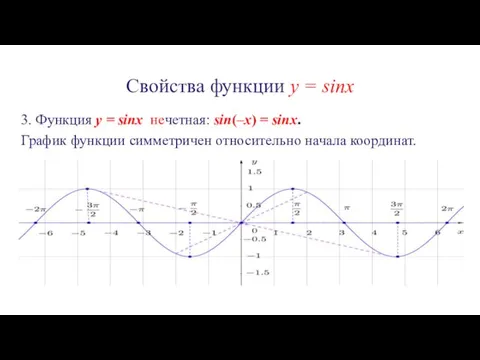
sinx.
График функции симметричен относительно начала координат.
Слайд 8Свойства функции y = sinx
4. Функция y = sinx периодическая.
Период функции равен
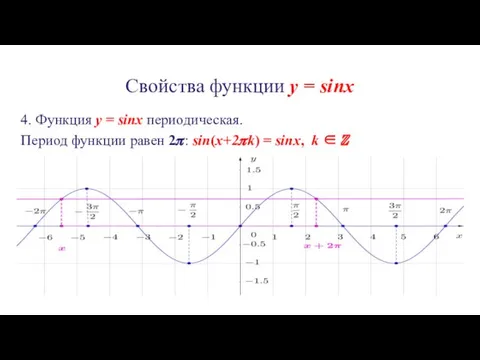
2?: sin(x+2?k) = sinx, k ∈ ℤ
Слайд 9Свойства функции y = sinx
5. Нули функции y = sinx: sinx =
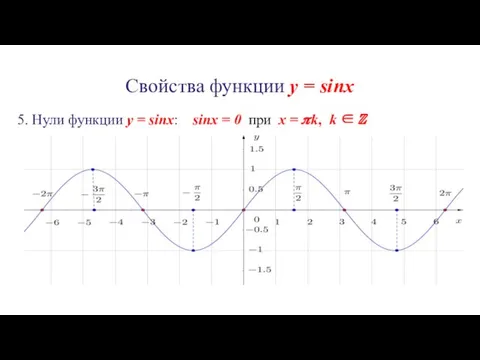
0 при x = ?k, k ∈ ℤ
Слайд 10Свойства функции y = sinx
6. Промежутки знакопостоянства функции y = sinx:
sinx >
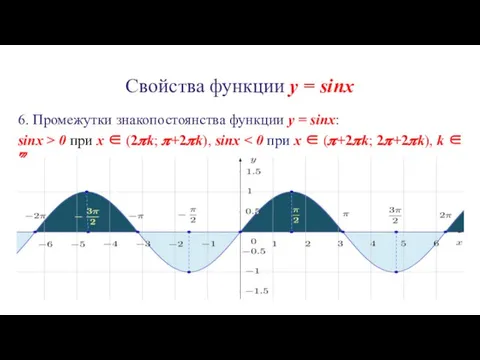
0 при x ∈ (2?k; ?+2?k), sinx < 0 при x ∈ (?+2?k; 2?+2?k), k ∈ ℤ
Слайд 11Свойства функции y = sinx
7. Промежутки монотонности и экстремумы функции y =
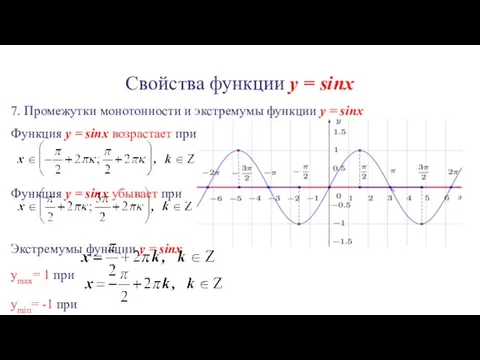
sinx
Функция y = sinx возрастает при
Функция y = sinx убывает при
Экстремумы функции y = sinx
ymax= 1 при
ymin= -1 при
Слайд 13Свойства функции y = cosx
1. Область определения функции y = cosx: D(cosx)
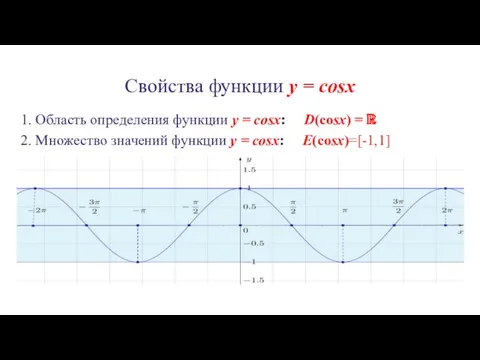
= ℝ
2. Множество значений функции y = cosx: E(cosx)=[-1,1]
Слайд 14Свойства функции y = cosx
3. Функция y = cosx четная: cos(–x) =
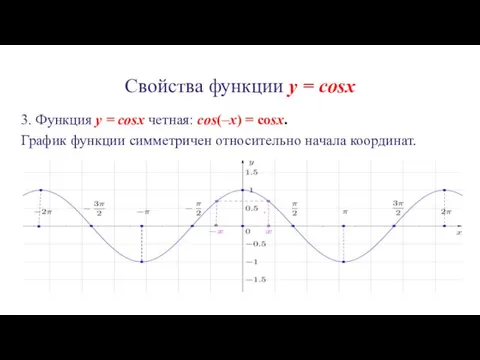
cosx.
График функции симметричен относительно начала координат.
Слайд 15Свойства функции y = cosx
4. Функция y = cosx периодическая.
Период функции равен
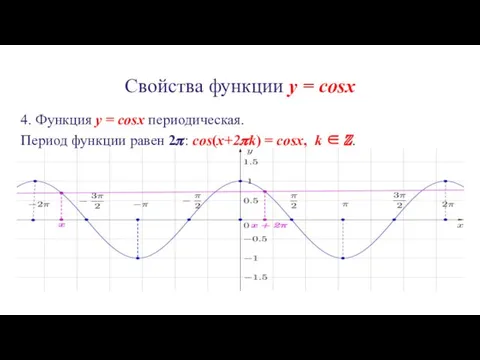
2?: cos(x+2?k) = cosx, k ∈ ℤ.
Слайд 16Свойства функции y = cosx
5. Нули функции y = cosx: cosx =
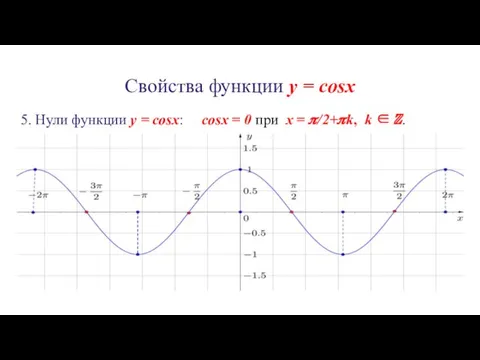
0 при x = ?/2+?k, k ∈ ℤ.
Слайд 17Свойства функции y = cosx
6. Промежутки знакопостоянства функции y = cosx:
cosx >
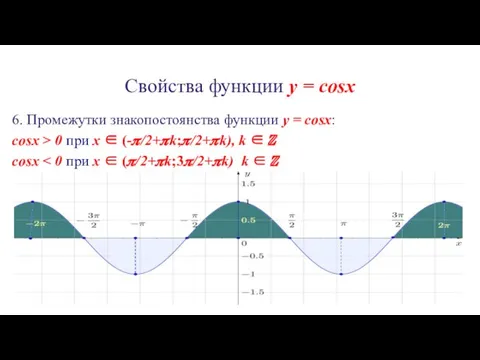
0 при x ∈ (-?/2+?k;?/2+?k), k ∈ ℤ
cosx < 0 при x ∈ (?/2+?k;3?/2+?k) k ∈ ℤ
Слайд 18Свойства функции y = cosx
7. Промежутки монотонности и экстремумы функции y =
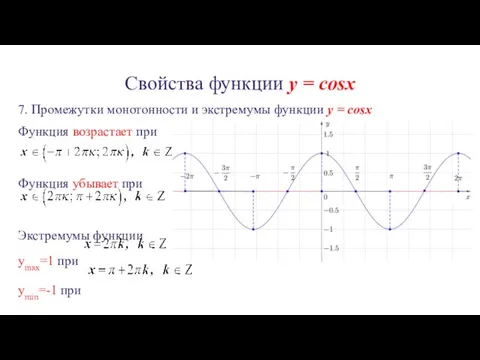
cosx
Функция возрастает при
Функция убывает при
Экстремумы функции
ymax=1 при
ymin=-1 при















 «Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе
«Арифметическая и геометрическая прогрессии» урок алгебры в 9 классе  Исследование математических моделей
Исследование математических моделей  Функции y=tg x и y=ctg x, их свойства и графики
Функции y=tg x и y=ctg x, их свойства и графики Построение графика квадратичной функции
Построение графика квадратичной функции Алгебра логики на практике
Алгебра логики на практике Тема урока: «Производные тригонометрических функций» Автор: учитель математики Гулова Римма Ивановна г.Старый Оскол 2011г.
Тема урока: «Производные тригонометрических функций» Автор: учитель математики Гулова Римма Ивановна г.Старый Оскол 2011г. Радианная мера углов и дуг
Радианная мера углов и дуг Презентация на тему Понятие и предмет международного частного права
Презентация на тему Понятие и предмет международного частного права  Презентация на тему Закономерности и особенности создания Древнерусского государства
Презентация на тему Закономерности и особенности создания Древнерусского государства  Основы логики Алгебра высказываний
Основы логики Алгебра высказываний Квадратная функция и ее график
Квадратная функция и ее график Пересечение и объединение множеств (8 класс)
Пересечение и объединение множеств (8 класс) Таблицы истинности
Таблицы истинности Функция y= ІхІ
Функция y= ІхІ Тема урока: Теорема синусов
Тема урока: Теорема синусов  Старая сказка на новый лад
Старая сказка на новый лад Презентация на тему Особенности прохождения гос. службы в правоохранит. органах
Презентация на тему Особенности прохождения гос. службы в правоохранит. органах  Презентация на тему Система высшего образования в Японии
Презентация на тему Система высшего образования в Японии  Выпуклость и вогнутость функции
Выпуклость и вогнутость функции Критические точки функции. Точки экстремумов
Критические точки функции. Точки экстремумов Свойства степени с натуральным показателем 7 класс
Свойства степени с натуральным показателем 7 класс Zadachi-na-smesi-i-splavy.ppt
Zadachi-na-smesi-i-splavy.ppt Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_
Заполните пропуски так, чтобы утверждения были верными - презентация по Алгебре_ Что такое функция? 7 класс Первый урок по теме «Функции» Составила учитель математики МОУ СОШ №2 Легенчук О.И.
Что такое функция? 7 класс Первый урок по теме «Функции» Составила учитель математики МОУ СОШ №2 Легенчук О.И.  Презентация на тему Огонь – твой друг и твой враг
Презентация на тему Огонь – твой друг и твой враг  Полиномы Одночлены Двучлены Трёхчлены Многочлены
Полиномы Одночлены Двучлены Трёхчлены Многочлены  Презентация на тему Контрольная карта Шухарта
Презентация на тему Контрольная карта Шухарта  Что такое функция 7 класс
Что такое функция 7 класс