Содержание
- 2. Цели: 06.07.2012 Повторить алгоритм построения графика линейного уравнения с двумя переменными. Рассмотреть линейную функцию и ее
- 3. 06.07.2012 www.konspekturoka.ru Алгоритм построения графика уравнения ах + bу + c = 0 3. Построим на
- 4. ах + by + c = 0 06.07.2012 www.konspekturoka.ru Вспомним! Выполним преобразования:
- 5. 06.07.2012 www.konspekturoka.ru y = kx + m Частный вид линейного уравнения с двумя переменными называется линейной
- 6. 06.07.2012 www.konspekturoka.ru Пример 1 Построить график функции у = 2х + 3, найти точку пересечения с
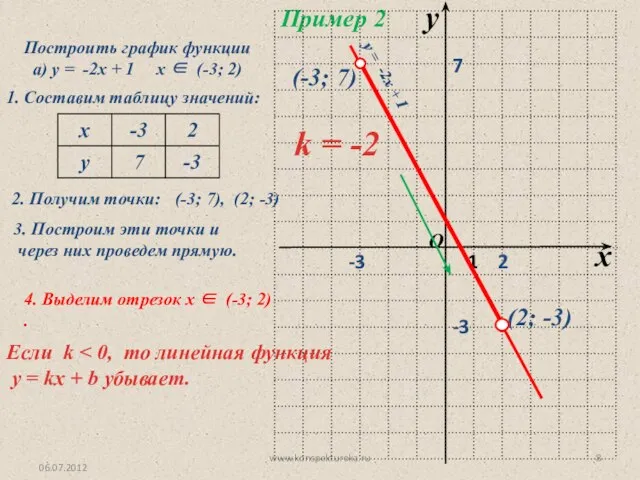
- 7. 06.07.2012 www.konspekturoka.ru Пример 2 Построить график функции а) у = -2х + 1 х -3;
- 8. 06.07.2012 www.konspekturoka.ru Пример 2 Построить график функции а) у = -2х + 1 х (-3;
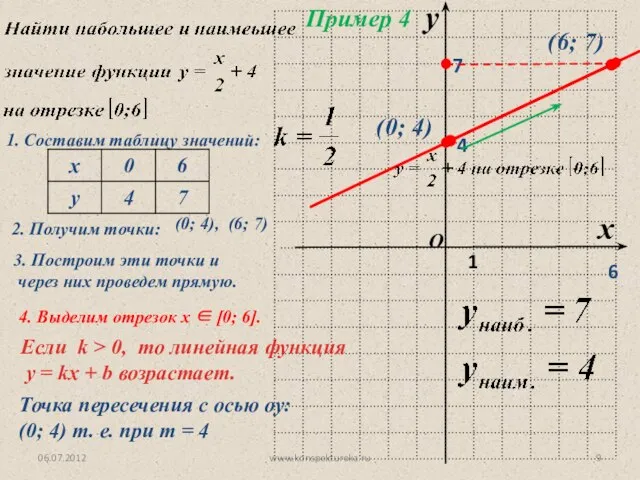
- 9. 06.07.2012 www.konspekturoka.ru Пример 4 1. Составим таблицу значений: 2. Получим точки: (0; 4), (6; 7) 3.
- 10. 06.07.2012 www.konspekturoka.ru Вывод: Функция y = kx + m называется возрастающей, если большему значению аргумента соответствует
- 11. 06.07.2012 www.konspekturoka.ru Вывод: Величина k определяет наклон графика функции y = kx + m Если k
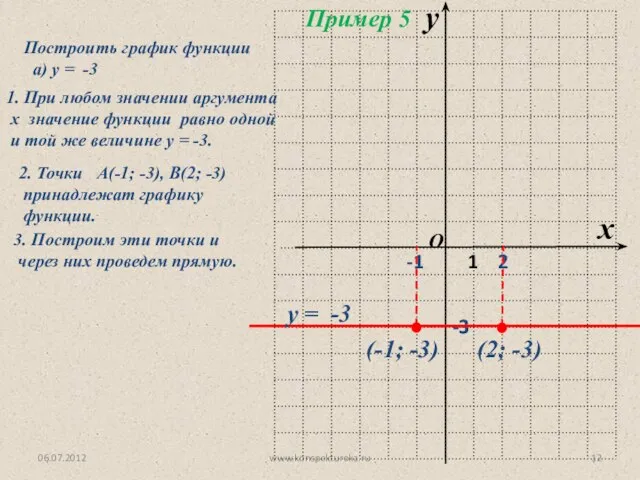
- 12. 06.07.2012 www.konspekturoka.ru Построить график функции а) у = -3 1. При любом значении аргумента х значение
- 14. Скачать презентацию








 Натуральные логарифмы
Натуральные логарифмы Действия с дробными числами
Действия с дробными числами Презентация на тему Понятие и предмет международного частного права
Презентация на тему Понятие и предмет международного частного права  Графический метод решения систем уравнений с двумя переменными
Графический метод решения систем уравнений с двумя переменными Линейная функция
Линейная функция  ГИА 2013 Модуль «Реальная математика» №17
ГИА 2013 Модуль «Реальная математика» №17 Пересечение и объединение множеств (8 класс)
Пересечение и объединение множеств (8 класс) Презентация на тему Особенности экспоненциального развития науки
Презентация на тему Особенности экспоненциального развития науки ЭВМ
ЭВМ Тема урока: Решение уравнений с параметром Урок формирования знаний и умений
Тема урока: Решение уравнений с параметром Урок формирования знаний и умений  Презентация на тему Система образования в Германии
Презентация на тему Система образования в Германии  Применение свойств функций к решению уравнений и неравенств
Применение свойств функций к решению уравнений и неравенств Производная степенной функции
Производная степенной функции  Процентные вычисления в жизненных ситуациях
Процентные вычисления в жизненных ситуациях Статистическое определение вероятности
Статистическое определение вероятности Урок: тригонометрические функции и их свойства
Урок: тригонометрические функции и их свойства Квадратный корень из степени 8 класс
Квадратный корень из степени 8 класс Презентация на тему Даниил Заточник
Презентация на тему Даниил Заточник Построение графика линейной функции вида у= kx + b
Построение графика линейной функции вида у= kx + b В лабиринте тригонометрических формул
В лабиринте тригонометрических формул Решение задач с помощью квадратных уравнений
Решение задач с помощью квадратных уравнений НЕРАВЕНСТВА (8 КЛАСС)
НЕРАВЕНСТВА (8 КЛАСС)  Квадратные уравнения
Квадратные уравнения Свойства функции У = sin x и ее график
Свойства функции У = sin x и ее график Презентация на тему Современные модели развития науки
Презентация на тему Современные модели развития науки  Презентация на тему дефицит и профицит государственного бюджета
Презентация на тему дефицит и профицит государственного бюджета Алгебраические дроби
Алгебраические дроби  Квадратичная функция. функция
Квадратичная функция. функция