Содержание
- 2. Свойства функции 1.D(y) 2.E(y) 3. Четность функции 4. Периодичность функции 5.Нули функции 6. Наибольшее значение 7.
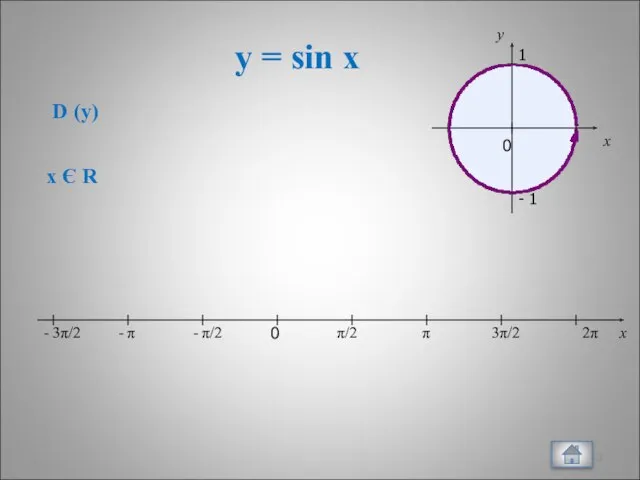
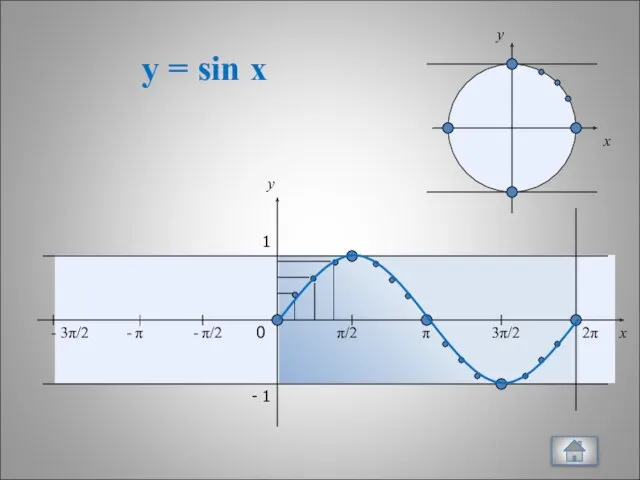
- 3. y = sin x x 0 π/2 π 3π/2 2π - π/2 - π - 3π/2
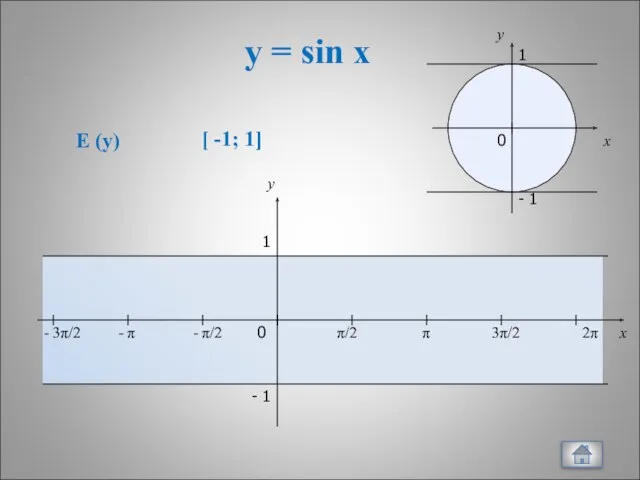
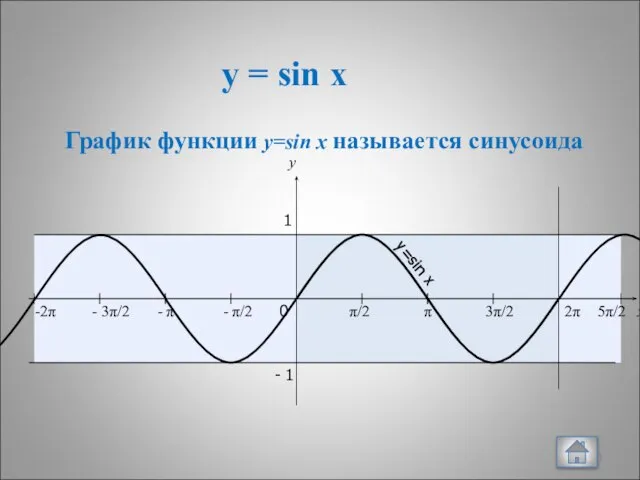
- 4. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
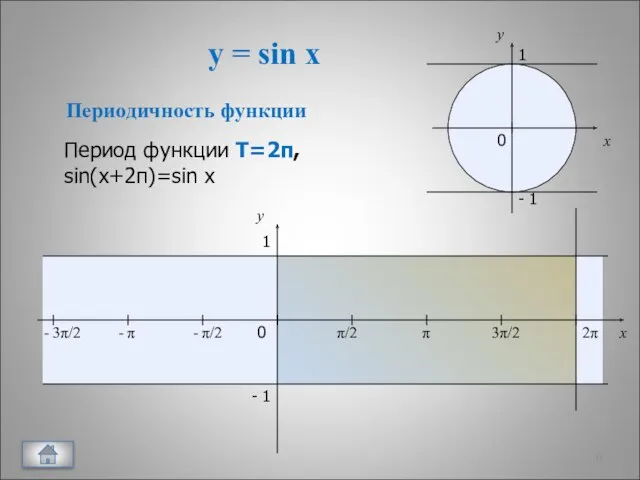
- 5. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
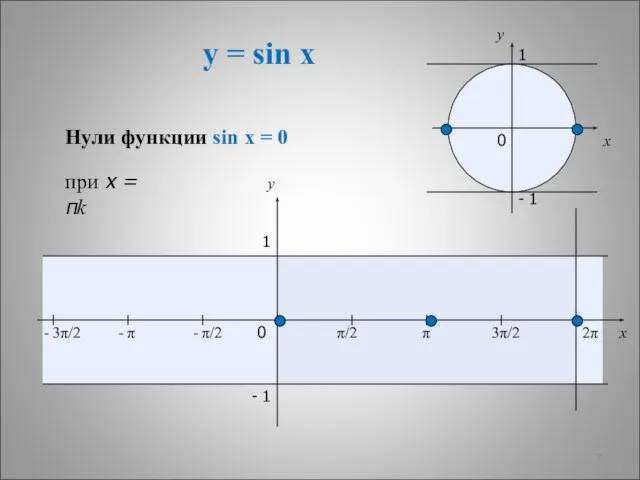
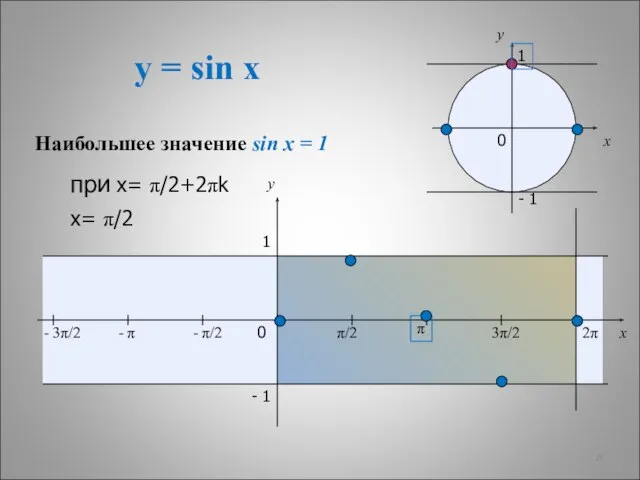
- 6. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
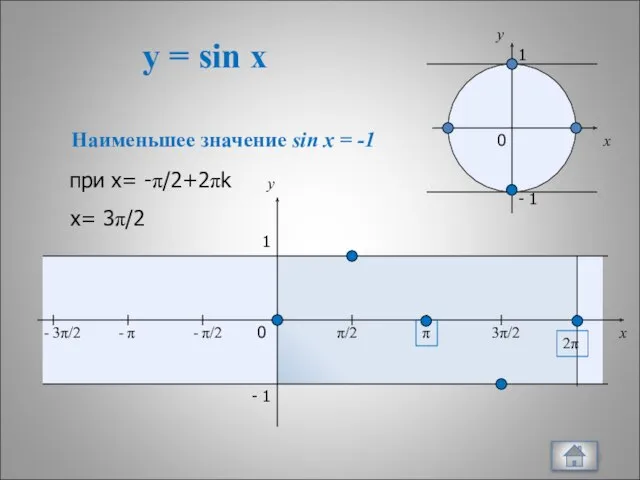
- 7. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 8. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 9. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
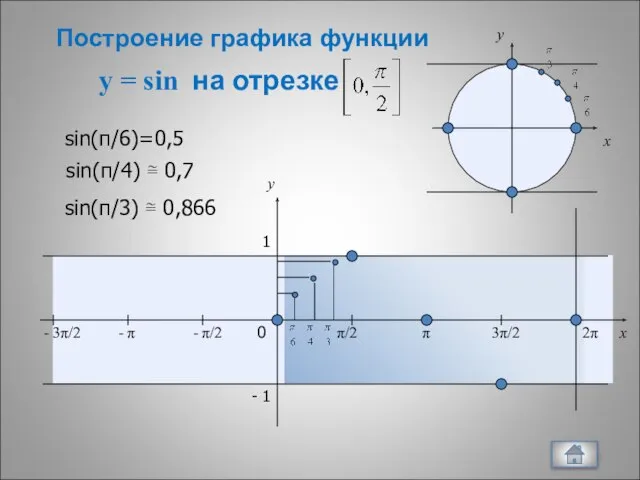
- 10. y = sin на отрезке x y 0 π/2 π 3π/2 2π x y 1 -
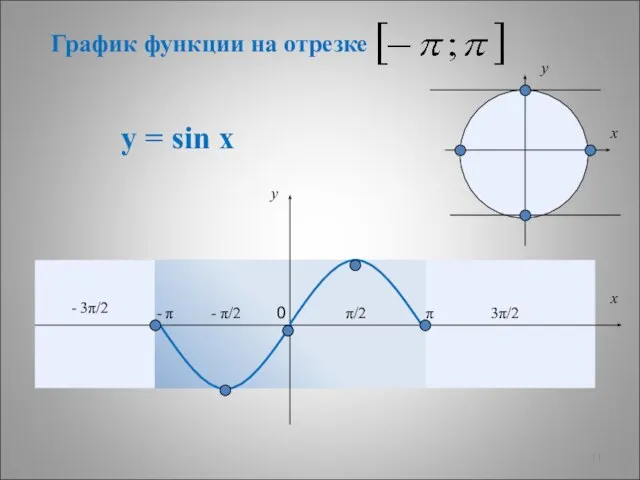
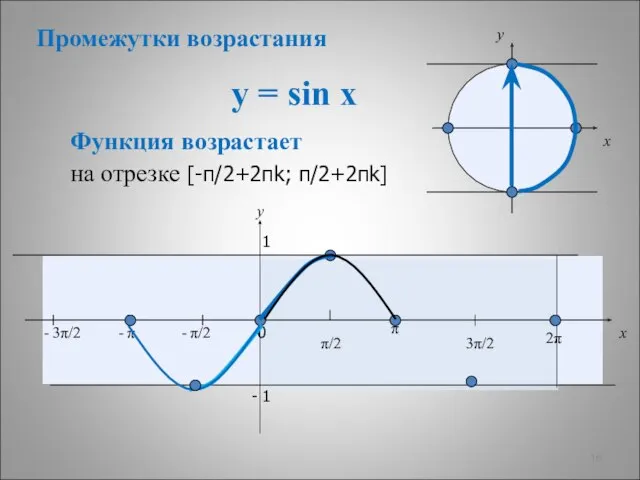
- 11. у = sin x π π/2 - π/2 - π - 3π/2 3π/2 y x 0
- 12. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 13. y = sin x x y 0 π/2 π 3π/2 2π 1 - 1 - π/2
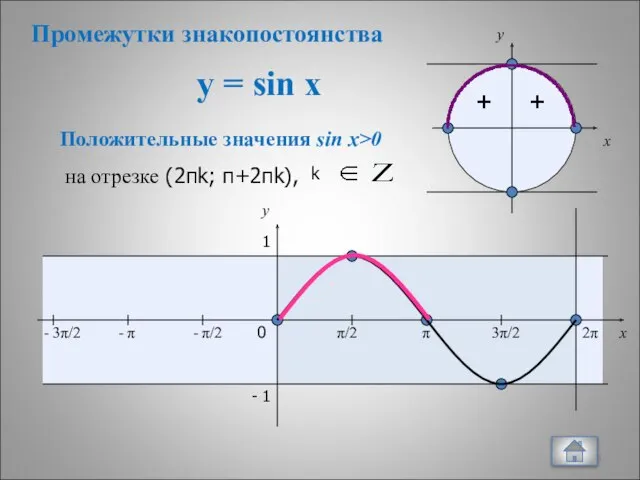
- 14. y = sin x + + x y 0 π/2 π 3π/2 2π x y 1
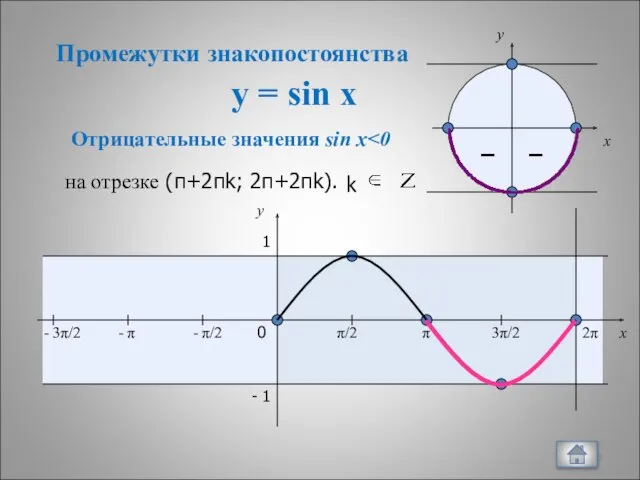
- 15. y = sin x – – x y 0 π/2 π 3π/2 2π x y 1
- 16. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 17. y = sin x x y 0 π/2 π 3π/2 2π x y 1 - 1
- 18. Сравнить числа sin 2 и sin 3 Задача Так как = 3,14, , то Из графика
- 19. Упражнения Пользуясь свойствами функции у = sin x , сравните числа: sin 1000 и sin 1300
- 20. Расположить в порядке возрастания числа sin 1.9 ; sin 3; sin(-1); sin(-1.5). Числа sin 1.9 и
- 21. Используя свойство возрастания или убывания функции y=sinx, сравните числа: и и и и 1 вариант 2
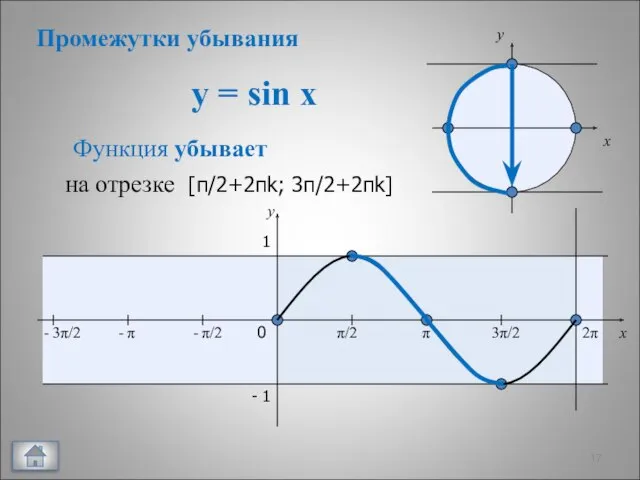
- 22. Разбить отрезок на два так, чтобы на одном из них функция у=sin х убывала, а на
- 23. № 722 Разбить данный отрезок на два отрезка так, чтобы на одном из них функция у=sinх
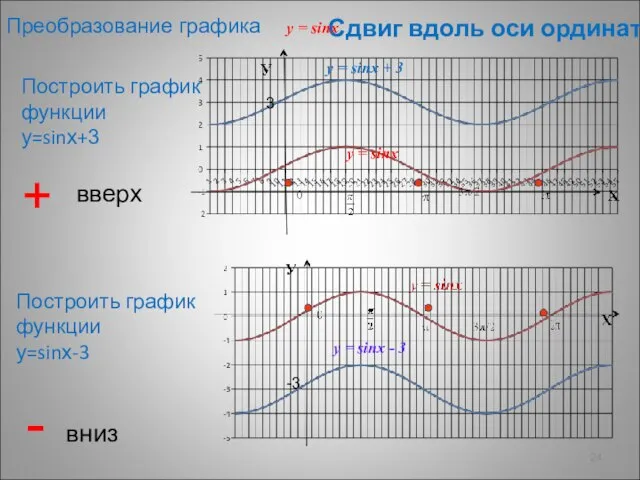
- 24. Сдвиг вдоль оси ординат Построить график функции у=sinх+3 Построить график функции у=sinх-3 + вверх - вниз
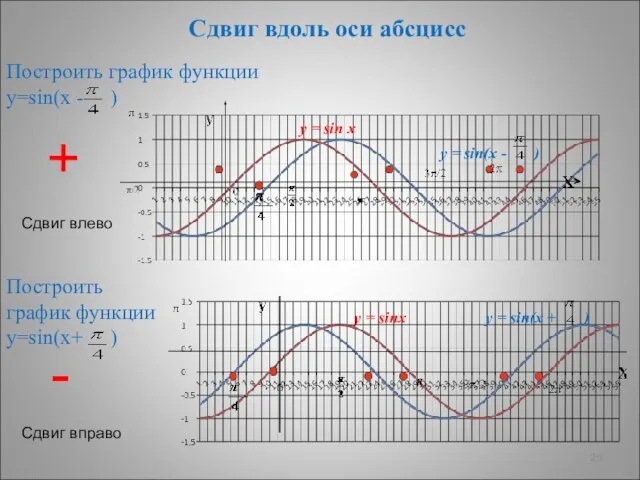
- 25. Сдвиг вдоль оси абсцисс Построить график функции у=sin(х - ) Построить график функции у=sin(х+ ) +
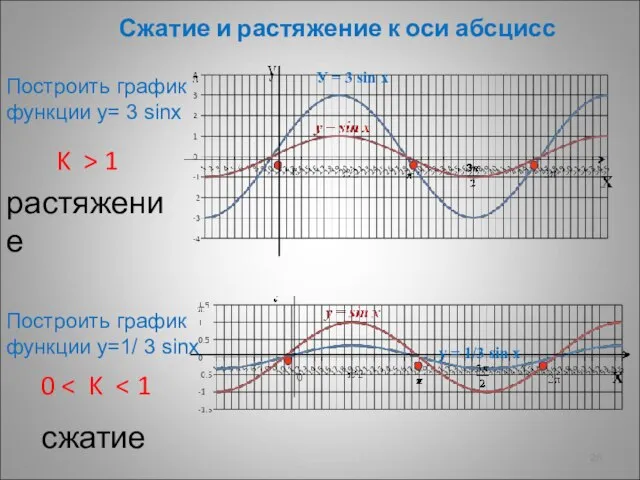
- 26. Сжатие и растяжение к оси абсцисс K > 1 растяжение 0 сжатие Построить график функции у=
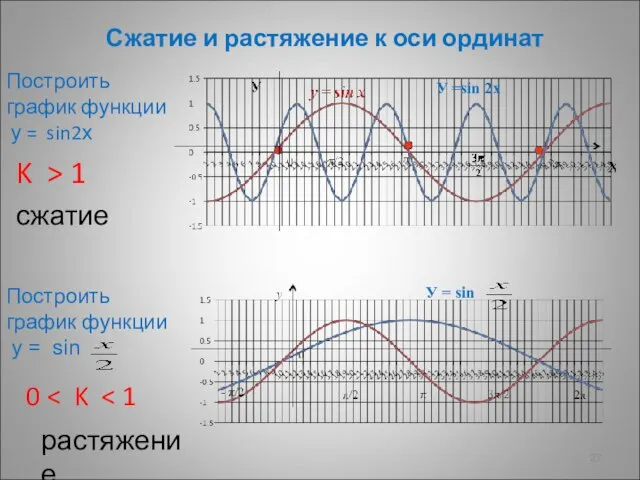
- 27. Сжатие и растяжение к оси ординат Построить график функции у = sin2х Построить график функции у
- 29. Скачать презентацию








 Всё о квадратном уравнении
Всё о квадратном уравнении Preobrazovanie-dvoynyh-radikalov.ppt
Preobrazovanie-dvoynyh-radikalov.ppt Презентация на тему Понятие и предмет международного частного права
Презентация на тему Понятие и предмет международного частного права  Буквенная запись свойств сложения и вычитания
Буквенная запись свойств сложения и вычитания Типы случайных событий и действия над ними
Типы случайных событий и действия над ними Решение квадратных уравнений Выполнили учителя Мкоу гимназии вятские поляны: Гатауллина гульфия анасовна и малькова надежда
Решение квадратных уравнений Выполнили учителя Мкоу гимназии вятские поляны: Гатауллина гульфия анасовна и малькова надежда  Классная работа. Пропорции. 11.01.13
Классная работа. Пропорции. 11.01.13 Старинные ЗАНИМАТЕЛЬНЫЕ задачи
Старинные ЗАНИМАТЕЛЬНЫЕ задачи Процентные вычисления в жизненных ситуациях
Процентные вычисления в жизненных ситуациях Логические законы и правила преобразования логических выражений
Логические законы и правила преобразования логических выражений Презентация на тему Принципы исторического исследования
Презентация на тему Принципы исторического исследования  Свойства арифметического корня П-ОЙ степени
Свойства арифметического корня П-ОЙ степени Квадратичная функция
Квадратичная функция  Презентация на тему Цели и задачи прокурорского надзора
Презентация на тему Цели и задачи прокурорского надзора  Тема: «Одночлены»
Тема: «Одночлены» Сумма «n» членов Арифметической прогрессии
Сумма «n» членов Арифметической прогрессии Применение свойств функций к решению уравнений и неравенств
Применение свойств функций к решению уравнений и неравенств Линейное уравнение с одним неизвестным
Линейное уравнение с одним неизвестным Презентация на тему Иоганн Готфрид Гердер
Презентация на тему Иоганн Готфрид Гердер Применения непрерывности Метод интервалов
Применения непрерывности Метод интервалов Степенная функция 9 класс учитель Ладошкина И.А.
Степенная функция 9 класс учитель Ладошкина И.А.  Прогрессии 9 класс
Прогрессии 9 класс Применение производной для исследования функции
Применение производной для исследования функции ГИА 2013 Модуль «АЛГЕБРА» №2
ГИА 2013 Модуль «АЛГЕБРА» №2 Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к
Функции и графики в школьном курсе математики ТМОМ Методика изучения основных разделов предметного содержания школьного к Модуль
Модуль Наименьшее общее кратное
Наименьшее общее кратное Логарифмическая функция и ее применение
Логарифмическая функция и ее применение