Разложение многочлена на множители способом группировки

Содержание
1) Вынесение общего множителя за скобки
2) Способ группировки
3)Маленькие исторические факты !!!
К содержанию

Вынесение общего множителя за скобки
Из каждого слагаемого, входящего в многочлен, выносится некоторый одночлен, входящий в качестве множителя во все слагаемые.
Таким общим множителем может быть не только одночлен, но и многочлен.

Алгоритм нахождения общего множителя нескольких одночленов
Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, - он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
Произведение коэффициента, найденного на первом шаге, является общим множителем, который целесообразно вынести за скобки.

Пример
Разложить на множители:
x4y3 - 2x3y2 + 5x2.
Воспользуемся сформулированным алгоритмом.
Наибольший общий делитель коэффициентов
–1, -2 и 5 равен 1.
Переменная x входит во все члены многочлена с показателями соответственно 4, 3, 2; следовательно, можно вынести за скобки x2.
Переменная y входит не во все члены многочлена; значит, ее нельзя вынести за скобки.
Вывод: за скобки можно вынести x2. Правда, в данном случае целесообразнее вынести -x2. Получим:
-x4y3-2x3y2+5x2=-x2(x2y3+2xy2-5).
К содержанию

Способ
группировки
Бывает, что члены многочлена не имеют общего множителя, но после заключения нескольких членов в скобки (на основе переместительного и сочетательного законов сложения) удается выделить общий множитель, являющийся многочленом.

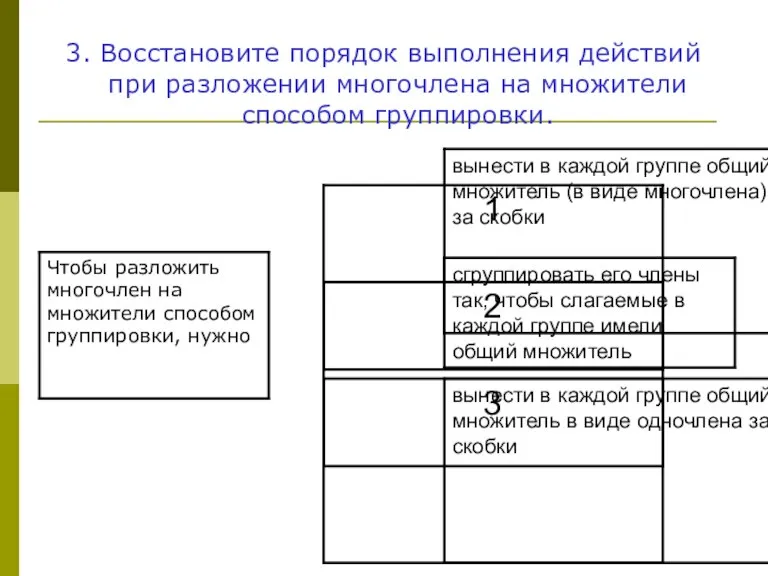
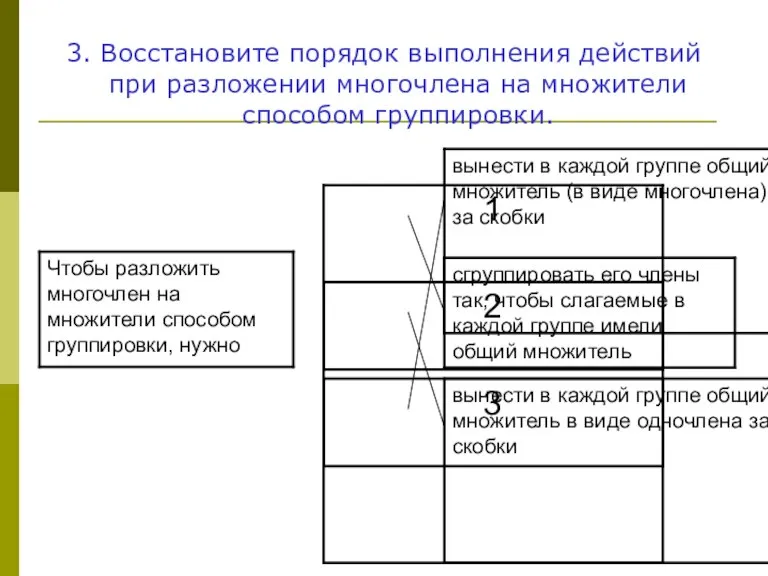
1. Сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель
2. Вынести в каждой группе общий множитель в виде одночлена за скобки
3. Вынести в каждой группе общий множитель (в виде многочлена) за скобки.
Алгоритм разложения многочлена на множители способом группировки:

Для уяснения сути способа группировки рассмотрим следующий пример:
разложить на множители многочлен
Xy–6+3x–2y

xy-6+3x-2y=
=(xy-6)+(3x-2y).
Пример не корректный !!!
Попробуйте применить другой способ !!!
Первый способ группировки:

Второй способ группировки
xy-6+3x-2y=(xy+3x)+(-6-2y)=
=x(y+3)-2(y+3)=
=(y+3)(x-2).

xy-6+3y-2y=(xy-2y)+(-6+3x)=
=y(x-2)+3(x-2)=
=(x-2)(y+3).
Третий способ группировки:

Разложение многочлена на множители с помощью комбинации различных приемов
В математике не так часто бывает, чтобы при решении примера применялся только один прием, чаще встречаются комбинированные примеры, где сначала используется один прием, затем другой и т.д. Чтобы успешно решать такие примеры, мало знать сами приемы, надо еще уметь выработать план их последовательного применения. Иными словами, здесь нужны не только знания, но и опыт. Вот такие комбинированные примеры мы и рассмотрим.

xy-6+3y-2y=(x-2)(y+3).
К содержанию
Вы уже поняли , что не всегда получается группировка с первого раза,если группировка не получилась попробуйте пойти иначе и решите пример другим способом _)))

А давайте Повторим !!!!

Определение

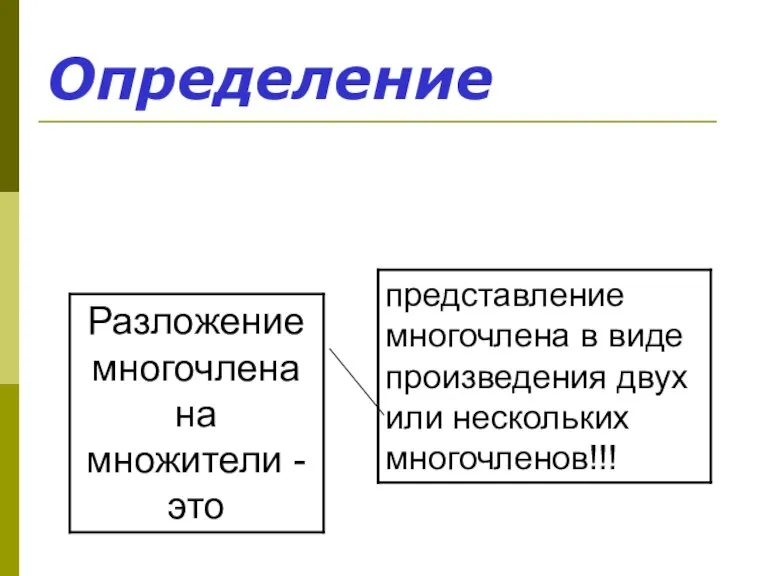
Завершите утверждение.
Представление многочлена в виде произведения одночлена и многочлена называется

2. Завершить утверждение.
Представление многочлена в виде произведения одночлена и многочлена называется вынесением общего множителя за скобки.

3. Восстановите порядок выполнения действий при разложении многочлена на множители способом группировки.

3. Восстановите порядок выполнения действий при разложении многочлена на множители способом группировки.

ИСТОРИЧЕСКИЕ ФАКТЫ !!!
Великие математики и
Ученые !!!

Известный математик по имени Эйлер (1707 - 1783 гг.) родился в Швейцарии. В 1727 г. двадцатилетним юношей он был приглашен в Петербургскую Академию наук. Этот математик был соратником Ломоносова. В Петербурге он попадает в круг выдающихся ученых математиков, физиков, астрономов, получает широкую возможность для создания и издания своих трудов (их у него было более 800, и заняли они 72 тома). Среди его работ - первые учебники по решению уравнений. Старшеклассники учатся по учебникам, прообразы которых создал этот ученый. Его считают великим учителем математики. Последние в научном мире он работал слепым, но продолжал работать, диктовал труды своим ученикам. Однако в научном мире он больше известен как физик, который построил точную теорию движения луны с учетом притяжения не только Земли, но и Солнца.