Содержание
- 2. Старинная русская задача Пошла баба на базар на людей посмотреть, да кое-что продать. Сколько надо бабе
- 3. Оптимизационные модели Оптимизационные модели используются в задачах, позволяющих выбирать из всех решений самый лучший оптимальный вариант.
- 4. Оптимизационная модель формируется в общем виде следующим образом: "Надо отыскать значения управляемых параметров (показателей) x1,x2,…..xn, придающие
- 5. Математическая модель задачи Параметры x1, x2, x3– число кур, уток и гусей соответственно, взятых бабой для
- 6. Установка надстройки Поиск решения в MS Excel 2007-2013
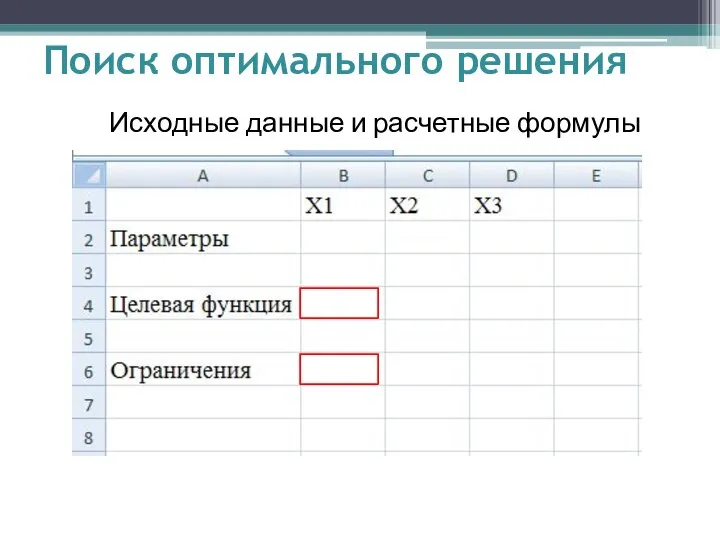
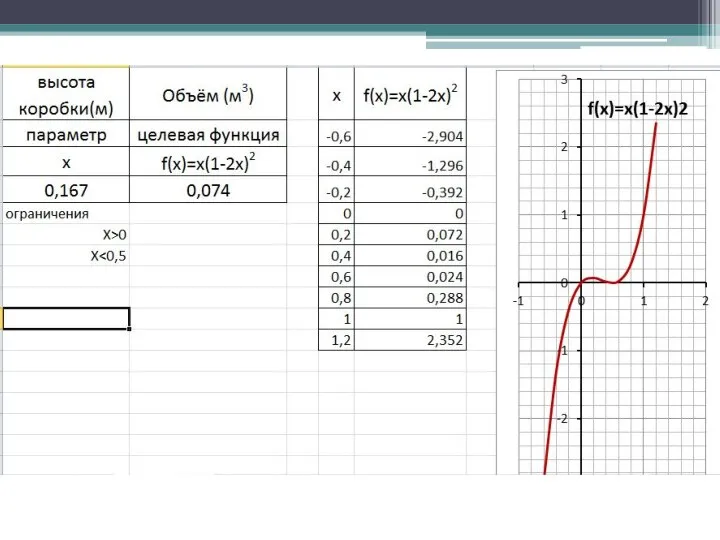
- 7. Поиск оптимального решения Исходные данные и расчетные формулы
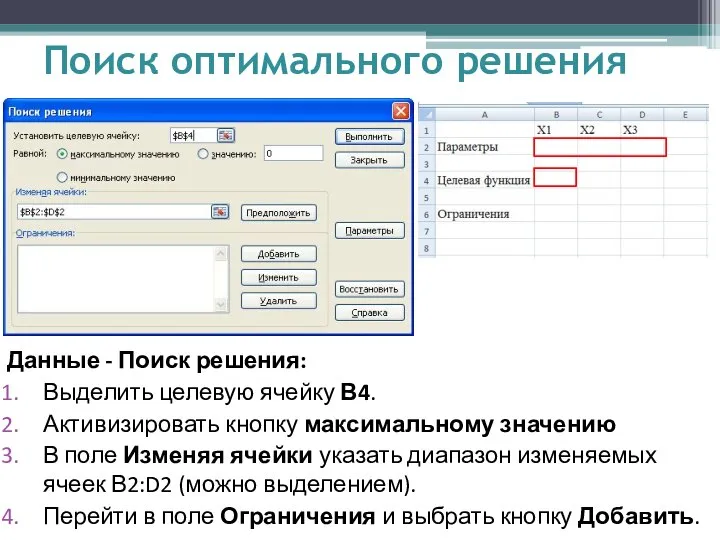
- 8. Данные - Поиск решения: Выделить целевую ячейку В4. Активизировать кнопку максимальному значению В поле Изменяя ячейки
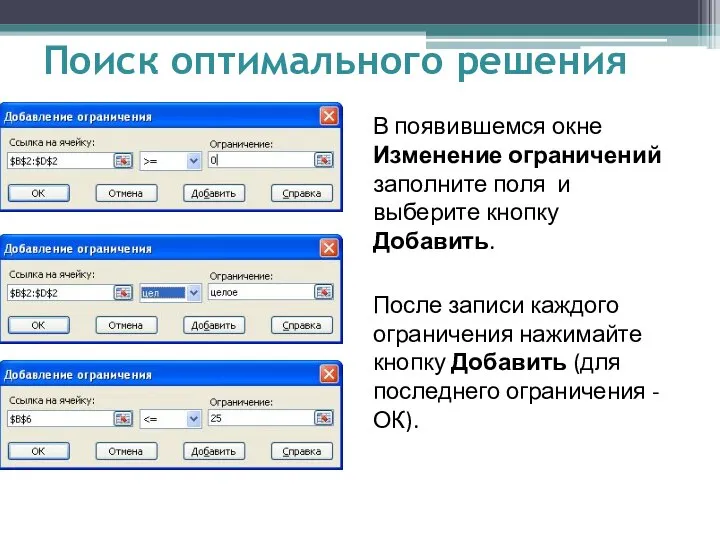
- 9. В появившемся окне Изменение ограничений заполните поля и выберите кнопку Добавить. После записи каждого ограничения нажимайте
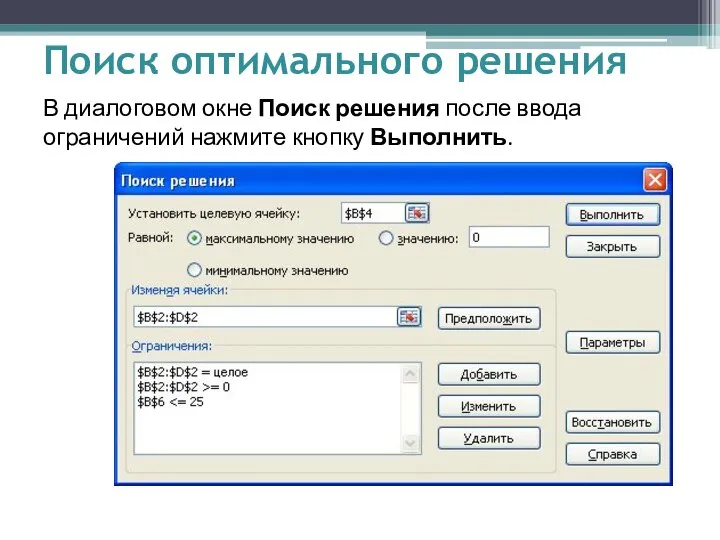
- 10. В диалоговом окне Поиск решения после ввода ограничений нажмите кнопку Выполнить. Поиск оптимального решения
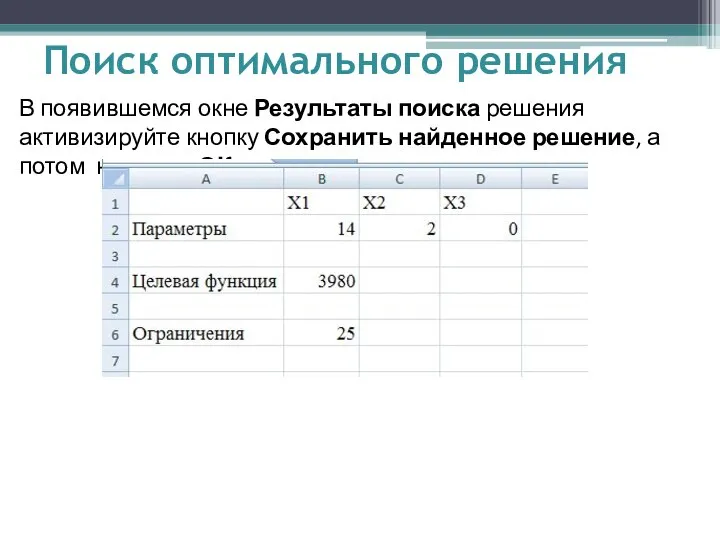
- 11. В появившемся окне Результаты поиска решения активизируйте кнопку Сохранить найденное решение, а потом нажмите ОК. Поиск
- 13. Задача 1: Фирма производит 2 модели (А и Б) книжных полок. Их производство ограничено количеством сырья
- 14. Пусть х – количество изделий модели А, у – кол-во изделий модели В. Тогда прибыль за
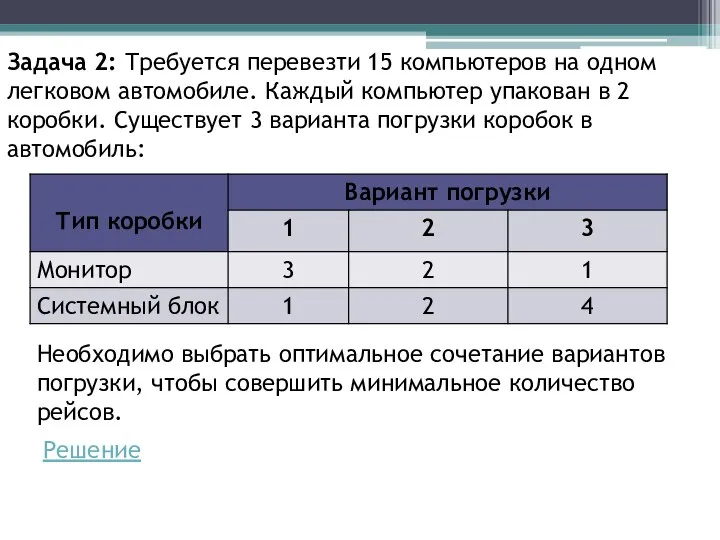
- 15. Задача 2: Требуется перевезти 15 компьютеров на одном легковом автомобиле. Каждый компьютер упакован в 2 коробки.
- 17. Скачать презентацию







 Интеграция и помощь мигрантам. Модуль 1. Выявление уязвимостей и потребностей в помощи
Интеграция и помощь мигрантам. Модуль 1. Выявление уязвимостей и потребностей в помощи Съезд регионального союза промышленников и предпринимателей Псковской области
Съезд регионального союза промышленников и предпринимателей Псковской области Введение в экономическую теорию
Введение в экономическую теорию Система жизнеобеспечения кочевников-казахов. Дисперсная организация производства и расселение населения
Система жизнеобеспечения кочевников-казахов. Дисперсная организация производства и расселение населения Главные вопросы экономики
Главные вопросы экономики Экспортный контроль сфу
Экспортный контроль сфу Экономические системы
Экономические системы Урок обобщения и повторения по теме Научно-техническая революция и мировое хозяйство
Урок обобщения и повторения по теме Научно-техническая революция и мировое хозяйство Лекция 3. Факторы производства
Лекция 3. Факторы производства Роль государства в рыночной экономике
Роль государства в рыночной экономике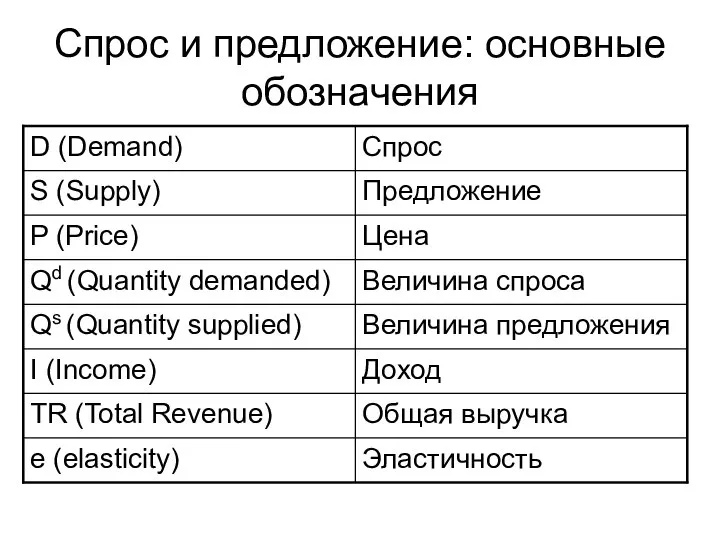 Спрос и предложение. Английские термины
Спрос и предложение. Английские термины Бизнес в России
Бизнес в России Проблемы управления и регулирования внешнего корпоративного долга Российской Федерации в условиях санкций
Проблемы управления и регулирования внешнего корпоративного долга Российской Федерации в условиях санкций Трудовые ресурсы фирмы
Трудовые ресурсы фирмы Экономическое планирование предприятия
Экономическое планирование предприятия Управление структурой капитала
Управление структурой капитала Продукция предприятия. (Тема 6)
Продукция предприятия. (Тема 6) Podaż turystyczna
Podaż turystyczna Теория спроса и предложения
Теория спроса и предложения История становления социального обеспечения в России на разных этапах развития
История становления социального обеспечения в России на разных этапах развития ФинЭк Анализ
ФинЭк Анализ Роль экономики в жизни общества и государства
Роль экономики в жизни общества и государства Реклама как двигатель торговли
Реклама как двигатель торговли Международные торги
Международные торги Россия в современном мире
Россия в современном мире Инфраструктурное обеспечение международного бизнеса Подготовили студенты группы Т-1202 Сембина А. Токманова С
Инфраструктурное обеспечение международного бизнеса Подготовили студенты группы Т-1202 Сембина А. Токманова С Отрасли обществознания (10 класс) (таблицы)
Отрасли обществознания (10 класс) (таблицы) Организация электроэнергетической службы на акционерном обществе агрофирма Волга
Организация электроэнергетической службы на акционерном обществе агрофирма Волга