Умозаключение и законы логики

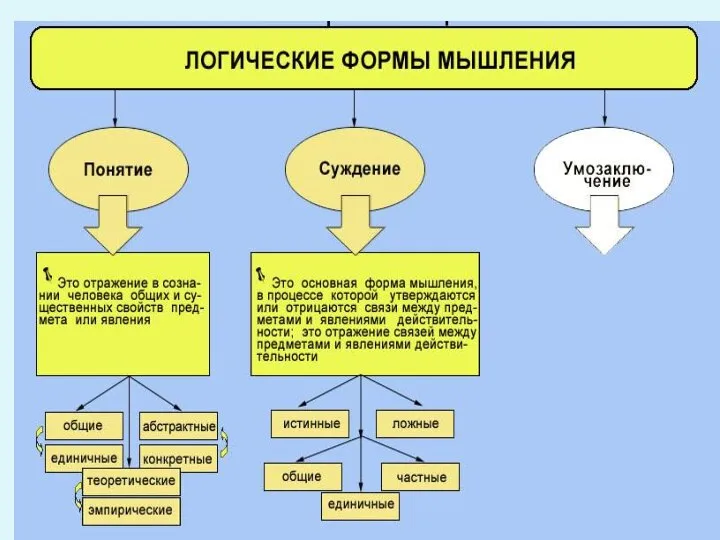
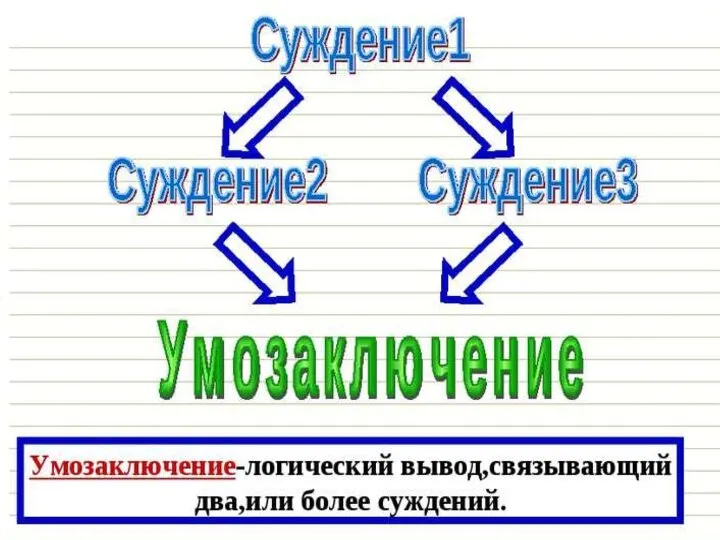
Умозаключение— это форма мышления, в которой из двух или нескольких суждений, называемых посылками, вытекает новое суждение, называемое выводом или заключением. Это форма мышления, посредством которой из ранее имевшейся информации выводится новая. Умозаключение осуществляется на основе предварительных знаний(суждений)и не зависит от получаемой в данный момент извне информации.

Умозаключение— это прежде всего выведение следствий. Каждый человек в своей жизни ежедневно строит разные умозаключения и получает следствия из этих заключений.

Как правило, вывод (заключение)
отделяется от посылок с помощью слов
«следовательно», «значит». Умозаключение с посылками р1, р2, …, рn и заключением Р можно записывать в виде: (р1, р2, …, рn) Р.

Преимущества умозаключения
Умозаключение непосредственно не затрагивает реальных предметов. Это важное свойство, так как зачастую нет возможности получить для наблюдения реальный предмет. Например, в астрономии положение планет определяется исходя из уже имеющихся знаний о движении небесных тел.

Недостатком умозаключения можно считать то, что зачастую выводы характеризуются абстрактностью и не отражают многих конкретных свойств, связей предмета. Часто нельзя говорить о правильности умозаключения до тех пор, пока оно не прошло проверку на практике.

Условия истинности умозаключения.
Посылки должны быть истинными суждениями и должны быть связаны между собой.
Например:
Все млекопитающие — животные.
Все кошки — млекопитающие.
Все кошки — животные.
(истинное умозаключение).
Невозможно сделать умозаключение из подобных суждений:
Все планеты – это небесные тела.
Все сосны являются деревьями.

Примеры ложных умозаключений
- Если число делится на 4, то оно делится на 2. Число 22 делится на 2. Следовательно, оно делится на 4.
- Все деревья являются растениями. Сосна – дерево. Значит, сосна – растение.
- Все учащиеся данного класса ходили в театр. Петя не был в театре. Следовательно, Петя – учащийся не данного класса.

Со временем человек обязательно побывает на Марсе. Иванов человек. Следовательно, Иванов со временем побывает на Марсе
(Здесь слово «человек» используется в двух разных смыслах(абстрактном и конкретном.)
Если 1 рабочий строит дом за 10 дней, то 10 рабочих его построят за1 день. Если 1 корабль пересекает Атлантический океан за 10 дней, 10 кораблей должны его пересечь за 1 день.(Смешаны разные явления.)

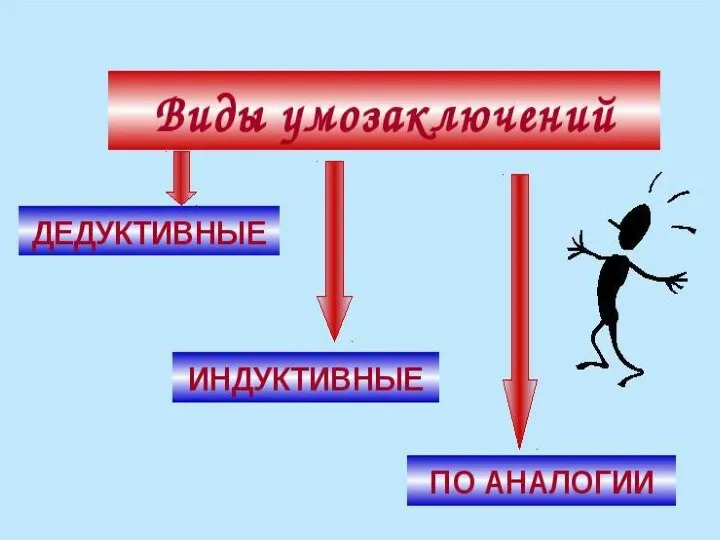
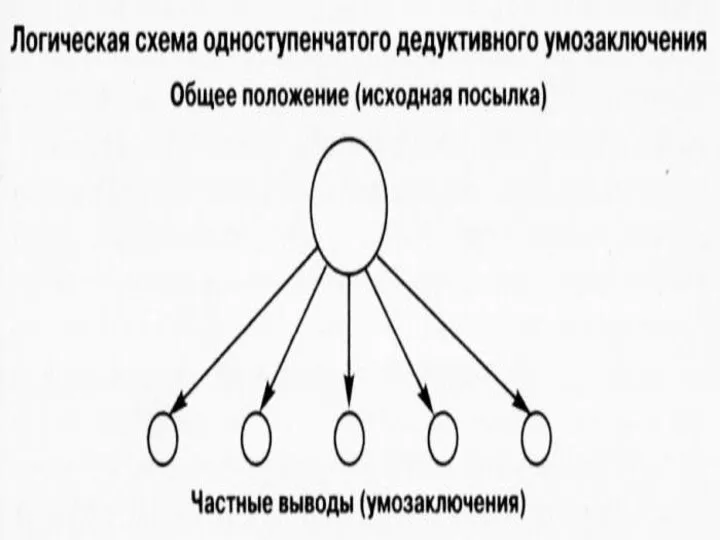
Умозаключения делятся на непосредственные и опосредованные
В непосредственных умозаключениях вывод делается из одной посылки:
«Все цветы являются растениями.
Некоторые растения являются цветами.
Верно, что все цветы являются растениями».
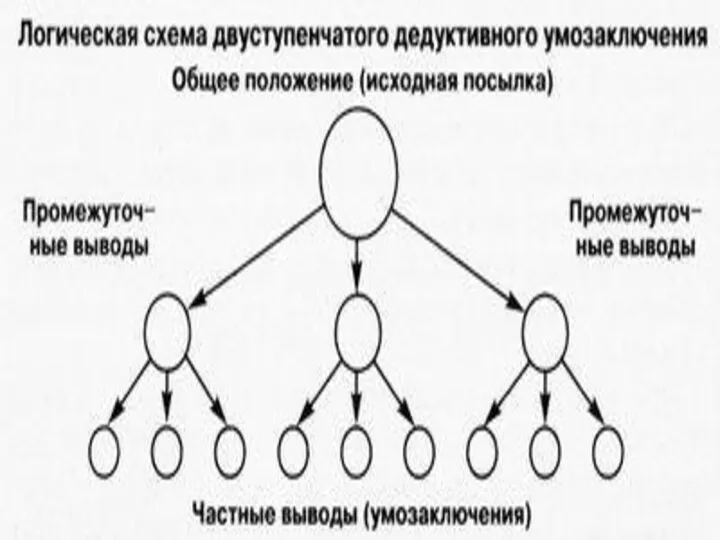
В опосредованных умозаключениях вывод делается из нескольких посылок.
«Все рыбы –это живые существа.
Все караси – это рыбы.
Все караси –это живые существа.»

Понятие силлогизма
Все дедуктивные умозаключения называются силлогизмами (от греческого syllogismos), что означает «выведение следствия».
Силлогизм бывает простым, сложным, сокращенным. Силлогизм, посылками в котором являются, простые категорические суждения, называется категорическим. Посылок в силлогизме две. Они содержат три термина силлогизма, обозначаемые буквами P , S и М. Р — это больший термин, S — меньший, а М — средний, связующий. S и Р связаны между собой средним термином (М).

Пример категорического силлогизма
Все газы(М) – это химические
элементы (Р).
Гелий (S) – это газ (М).
Гелий (S) - это химический
элемент (Р).

Доказательная аналогия

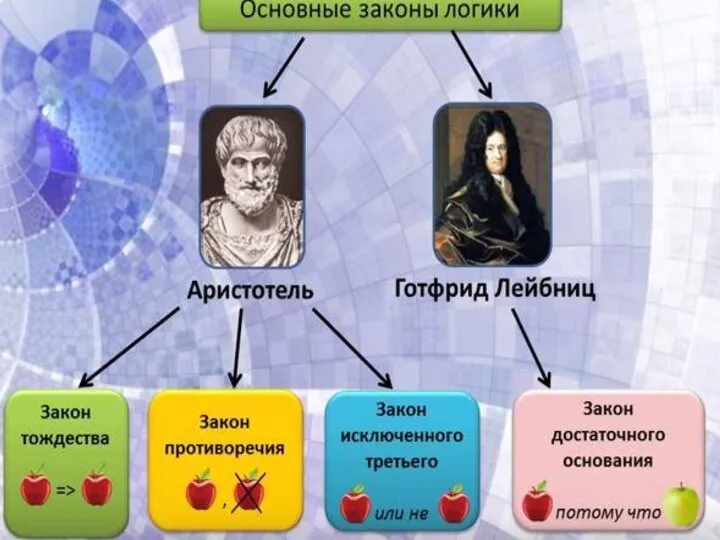
Закон тождества, непротиворечия и исключенного третьего
были открыты Аристотелем. Закон достаточного основания был открыт Лейбницем. Они являются столпами логики, без этих законов логика немыслима.
Логические законы — это необходимые правила построения непротиворечивого мышления.

Закон тождества (a = a)
Под тождеством понимают равнозначность, одинаковость. Редко можно говорить об абсолютном тождестве. Но можно говорить о тождестве, отстраняясь от полной абстракции. Закон тождества означает, что в процессе построения суждений, высказываний недопустимо подменять один предмет другим. То есть, нельзя произвольно заменять предмет, с которого логическое построение было начато, на другой.

Нарушения закона тождества
проявляется в «подмене понятия»,что означает потерян предмет понятия, т. е. первоначально понимаемое значение изменилось.
И в подмена тезиса. Это означает изменение первоначально
понимаемого тезиса в процессе дискуссии.

ЛЮБОЕ УТВЕРЖДЕНИЕ ДОЛЖНО ИМЕТЬ ОСНОВАНИЕ.
Достаточным основанием является достоверная информация.
Для математики это выражения, выведенные при помощи аксиом, теорем.
Достоверным будет считаться и информация, полученная на основе научных законов.
Для обоснования нового суждения можно использовать выведенные ранее суждения.