Связь ДПФ и ДВПФ

Тема:
Связь ДПФ и ДВПФ.

Восстановление ДВПФ по коэффициентам ДПФ
N −1
Связь ДВПФ и ДПФ
Пусть x(k) – N-точечная последовательность. ДВПФ этой последовательности (при
Δt = 1 )
X (ν) = ∑ x(k )e − j 2πν k ,
k = 0
где ν = f Δt = f / fд – нормированная частота (доли частота дискретизации). Используя фор- мулу обратногоДПФ, получим
.
N
N
N −1 N −1 N −1
N −1
j 2π nk
− j 2π(ν− n ) k
− j 2πν k
X (ν) = ∑[ ∑ XN (n) e ] e = ∑ XN (n) ∑ e
k = 0 n = 0 n = 0 k = 0
Просуммируем N членов геометрической прогрессии:
n
N N
N
− j 2π(ν − ) k
N
N
n
sin π(ν − n )N
− jπ(ν − ) ( N −1)
= e N N .
sin π(ν − n )
N
Поэтому для X (ν) можем записать
n
− j 2π(ν − n ) N − jπ(ν − n ) N
sin π(ν − n )N
e
N −1
k = 0
e
− j 2π(ν − n ) − jπ(ν − n )
1− e
=
1− e = e
⋅ N =
sin π(ν − )
N
∑
N
N −1
X (ν) = ∑ X
n = 0
n
(n) N e − jπ(ν− N ) ( N −1).
sin π(ν − n )N
n
N
sin π(ν − )
(1)
X (ν) по коэф-
,
Это интерполяционная формула восстановления континуальной функции фициентам ДПФ, вычисленным без масштабирующего множителя:
N −1
k = 0
− j (2π/ N ) nk
XN (n) = ∑ x(k) e
В точках ν= n / N имеет место
X (nΔν) = XN (n), Δν = 1/ N.
(2)
Таким образом, коэффициенты ДПФ XN (n) можно рассматривать как отсчёты функции
X (ν) , взятые с шагом Δν = 1/ N в соответствии с теоремой отсчётов в частотной области.
На рис. 1а представлен одиночный импульс конечной длительности и модуль его спек- тра. Рисунок 1б показывает, что периодическому повторению импульса с периодом T со-
ответствует дискретизованная версия непрерывного спектра. Отдельные отсчёты связаны с коэффициентами ряда Фурье Cn простым соотношением
X (nΔf )
1 T /2
T
T −T /2
j 2π nt
Cn = ∫ x(t) e dt = Δf X (nΔf ), Δf = 1/ T.

⎨
Рис. 1
Дискретизация импульса с шагом Δt приводит к периодическому повторению его спектра с пе- риодом fд = 1/ Δt (по нормированной частоте с периодом 1). Дискретная последовательность x(k ) и её непрерывный спектр (ДВПФ) X (ν) показаны на рис. 1в. Наконец, периодическому повторе-
нию последовательности x(k ) с периодом N соответствует дискретизованная версия непрерывной функции X (ν) с шагом Δν = 1/ N. Отдельные дискреты этой функции связаны с коэффициентами ДПФ соотношением (2). Эта связь иллюстрируется на рис. 1г.
Дискретное время и дискретная частота – именно это свойство ДПФ (а также существование быстрых алгоритмов БПФ) объясняет его повсеместное распространение в цифровых системах обработки сигналов.
Интерполяция добавлением нулевых отсчётов
Иногда качество визуализации ДВПФ X (ν) с помощью ограниченного набора из N коэффици- ентов ДПФ может оказаться недостаточным (рис. 1в, г). Практический способ увеличения числа отсчётов функции X (ν) состоит в следующем. Определим новую последовательность y(k) дли-
ной в M отсчётов( M > N ) путём дополнения исходной последовательности x(k ) нулевыми отсчё- тами. Число таких нулевых отсчётов будет M − N:
y(k) = ⎧ x(k), 0 ≤ k ≤ N −1,
⎩0, N ≤ k ≤ M −1.
Для этой последовательности отсчётные значения функции X (ν) в точках
νm = m / M , m = 0, 1,
, M −1, взятые с новым шагом Δν = 1/ M , будут
M −1
X (νm ) = ∑ y(k) e − j 2πmk /M .
(3)
k = 0
Это выражение с точностью до множителя Δt / M представляет собой М-точечное ДПФ, кото- рое может быть вычислено, например, с использованием быстрых алгоритмов. Характерно, что если взять M = 2N , то дополнительные отсчёты X (νm ) будут расположены между N первоначаль-
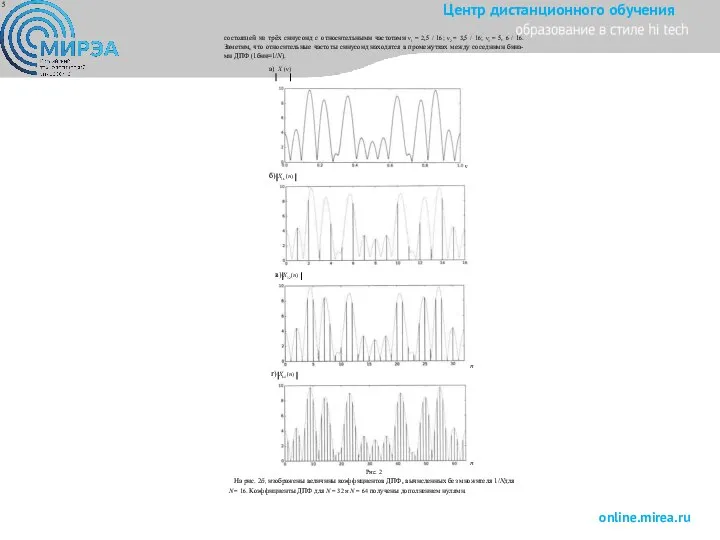
ными. При этом улучшается качество визуализации спектральной функции X (ν), которая остаётся неизменной от такого дополнения, так как она определяется первоначальной длиной массива x(k). Следующий пример иллюстрирует такую возможность. На рис. 2а представлено непрерывное изображение X (ν) на периоде[0, 1] для 16-точечной последовательности
x(k) = sin 2π(2,5 / 16)k + sin[2π(3,5 / 16)k + sin 2π(5, 6 / 16.)k,

состоящей из трёх синусоид с относительными частотами ν1 = 2,5 / 16; ν2 = 3,5 / 16; ν3 = 5, 6 / 16. Заметим, что относительные частоты синусоид находятся в промежутках между соседними бина- ми ДПФ (1бин=1/N).
а) X (ν)
ν
б) X16 (n)
в)
n n n
в) X32 (n)
n
г) X64 (n)
n
Рис. 2
На рис. 2б, изображены величины коэффициентов ДПФ, вычисленных без множителя 1/Nдля
N = 16. Коэффициенты ДПФ для N = 32 и N = 64 получены дополнением нулями.

Примеры решения задач на ДПФ
Гармонический сигнал x(t) = cos 2πf0t дискретизуется так, что на периоде образу-
∙
ется 8 отсчетов.
1.
2.
15
Изобразить последовательность x(k) и ее спектр.
Найти и изобразить по модулю ДВПФ и ДПФ последовательности
y(k) = ∑ x(m)1(k − m) и .
m=0
Решение 1. x(k) = cos 2πf0kΔt = cos 2πν0k, ν0 = f0Δt = f0 / fд − частота косинусоиды, нормированная к частоте дискретизации (доли частоты дискретизации). Спектр дискрети- зованной косинусоиды – две дельта-функции (с весом ½)в точках ±ν0 , повторяющиеся с периодом 1.
0 0
0
2 2
косинусоиды. С учетом того, что cos 2πν k = 1 exp( j2πν k) + 1 exp(− j2πν k) можем записать
для ДВПФ последовательности y(k)
( )
( )
0
0
1
2
2
N −1 N −1
.
1 sin π(ν + ν ) N
1 sin π(ν − ν ) N
= e− jπ(ν+ν0 )(N −1) ⋅ 2 + e− jπ(ν−ν0 )(N −1) ⋅ 2
sin π(ν + ν0 )
sin π(ν − ν0 )
⎡
− j2π(ν+ν0 )k ⎤
N −1 1 ⎡N −1
− j2π(ν−ν0 )k ⎤
Y ν =
1 k − m e
+
1 k − m e
⎢
⎥
⎢
⎥ =
m=0 ⎣k =0
⎦ m=0 ⎣k =0
⎦
( ) ∑ ∑
∑ ∑
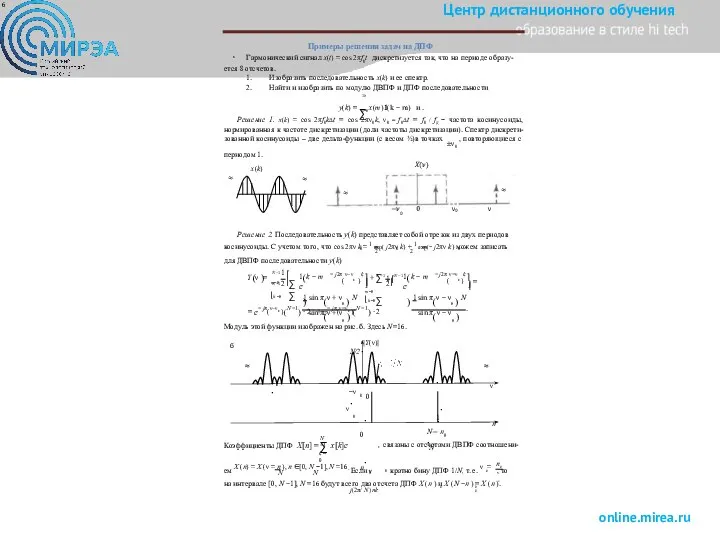
Модуль этой функции изображен на рис. б. Здесь N=16.
,
N −1
k = 0
Коэффициенты ДПФ X[n] = x[k]e
∑
связаны с отсчетами ДВПФ соотношени-
0
ем X (n) = X (ν = n ), n ∈[0, N −1], N =16. Если ν
0
0
n
N N
кратно бину ДПФ 1/N, т. е. ν = , то
0 0 0
*
на интервале [0, N −1], N =16 будут всего два отсчета ДПФ X (n ) и X (N −n ) = X (n ).
x(k)
≈
≈
≈
≈
−?0 0 ν0 ν
Решение 2. Последовательность y(k) представляет собой отрезок из двух периодов
X(?)
ν
|Y(ν)|
N∕2
·
б
≈
≈
−1·
n
· 1·
N−·n0 ·N
0· n· 0
j(2π/ N )nk
·−ν·0 0 ν·0

Решение избранных задач из курсовой письменной работы 16 октября 2017 г.
Найти и изобразить по модулю ДВПФ N - точечных последовательностей
N
N −1
x k = 1 k − m
m=0
⎜ ⎟
⎝
⎠
( ) ∑ ( ) и y (k ) = x (k )cos⎛ 2πlk ⎞.
Для последовательности
x (k )
( )
( )
( )
N −1 N −1
N −1
m=0
− j 2πνk
− j2πνN
− j2πν N −
1 sin πνN
− j2πνm
− j2πν
1 k
N −1 N −1
− j 2πνk
1− e
sin πν .
1− e
= e
= e
⎡
X ν =
m e
k =0 ⎣m=0
( ) ∑ ⎢ ∑
⎤
⎡
⎤
=
1 k − m e
=
⎥
⎦ m=0 ⎣k =0
∑ ⎢ ∑
⎥
⎦
=
⋅
∑
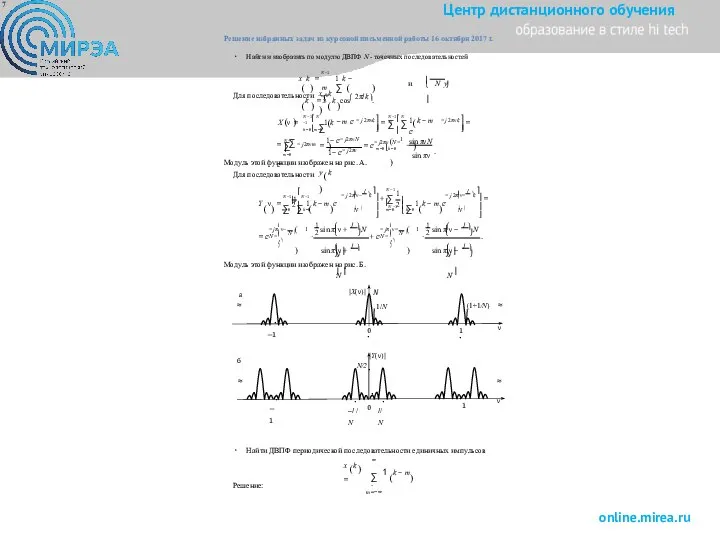
Модуль этой функции изображен на рис. А.
Для последовательности
y (k )
( )
( )
1
1
1
2
1 sin π⎛ν + l ⎞ N
2
1 sin π⎛ν − l ⎞ N
sin π⎛ν + l ⎞
sin π⎛ν − l ⎞
⎜ N ⎟
⎜ N ⎟
N
⎛ l ⎞
N
⎛ l ⎞
⎜ N ⎟
⎜ N ⎟
⎜ N ⎟
⎝ ⎠
⎝ ⎠
N −1 1 ⎡N −1
− j 2π⎛ν+ l ⎞k ⎤
N −1 ⎡N −1
− j 2π⎛ν− l ⎞k ⎤
⎜
⎟
⎜
⎟
⎝ ⎠
− jπ ν+ N −
= e
⎝ ⎠
− jπ ν− N −
e
+
=
m=0 2 ⎢ k =0
m=0 2 ⎢ k =0
⎣
⎥
⎥
⎦
⎣
⎥
⎥
⎦
Y (ν) = ∑ ⎢ ∑ 1(k − m)e
⎝
⎠
⎝
⎠
⋅
⋅
⎝ ⎠
⎝
⎠
⎜ N ⎟
∑
⎢ ∑ 1(k − m)e
.
Модуль этой функции изображен на рис. Б.
Найти ДВПФ периодической последовательности единичных импульсов
∞
x (k ) =
∑ 1 (k − m) .
m=−∞
Решение:
ν
1/N
|X(ν)|
(1+1∕N)
N
0·
≈
а
≈
·
−1
1·
N∕2
ν
·
0
|Y(ν)|
·
б
≈
≈
–l·/N
l/·N
−·1
·1

X (ν) =
( )
m=−∞ k=−∞
∞ ∞
∞ ∞
− j2πν
⎡ ⎤
=
⎥
k =−∞ ⎣m=−∞ ⎦
∑ ⎢ ∑
1 k − m e
k ∑ ∑ 1 (k − m) e− j2πνk
С учетом теоремы запаздывания ДВПФ имеем
e− j2πνm
∞
X (ν) = ∑
m=−∞
Это есть ряд Фурье для периодической (по частоте) последовательности δ - функций с пе- риодом 1. Действительно
C
∞ ∞
e− j2πνn
−n
∑ δ(ν − n) =
m=−∞
∑
m=−∞
Где коэффициенты Фурье
( )
1
2
j2πνn
C = δ ν e
− 12
dν ≡ 1
−n ∫
Таким образом
X (ν) =
δ(ν − n)
∞
e− j2πνm =
∑
m=−∞
∞
n=−∞
∑
Для θ = ωΔt = 2πf Δt = 2πνможем записать
X (θ) =
δ(θ − 2πn)
∞
e− jmθ =2π
∑
m=−∞
∞
n=−∞
∑
Найти обратное ДВПФ для функции
∞
X (θ) = ∑ cos θm ,
m=−∞
где θ = ωΔt = 2πf Δt = 2πν, Δt − шаг дискретизации . По формуле Эйлера
∞ ∞
cosθm=
1 ⎡e− jθm + e jθm ⎤
2 ⎣ ⎦
∑
m=−∞
∑
m=−∞
.
k
θ
x(k)
x(k)
-3 -2 -1
0 1 2 3 k
-3 -2
-1 0 1 2
3 ν
X(ν)
X(θ)
ДВПФ
ДВПФ
~
~
~
~
~
~
~
~
−2π 0 2π
·

Основы цифровой обработки сигналов; лекция 20 ноября 2017; МФТИ
В предыдущей задаче было показано
∞ ∞
n=−∞
e− jθm =2π
∑
m=−∞
∞
∑ δ(θ − 2πn) ∑ 1 (k − m) .
m=−∞ ДВПФ
Поэтому
2
2
∞
∞
∞
m=−∞
x (k ) = 1
∑
m=−∞
∑
1 (k − m)+ 1
∑ 1 (k − m) =
m=−∞
1 (k − m) .
ЗАДАЧИ
1. Пусть
x(k) и пусть
11
N
j 2πnk
k =0
X (n) = ∑ x(k)e
-12-точечное ДПФ действительной последовательности
X (0) = 10, X (1) = −5 − j4, X (2) = 3 − j2, X (3) =1+ j3, X (4) = 2 + j5, X (5) = 6 − j2, X (6) = 12
Не вычисляя обратного ДПФ, определить
2
11 11 j 2π k 11
k =0 k =0 k =0
a) x(0), b) x(6), c) ∑ x(k), d ) ∑ e 3 x(k), e) ∑ x(k)
2.
Пусть x (k ) – N-периодическая последовательность. Тогда 3N тоже можно считать
её периодом. Пусть X (n) – коэффициенты ДПФ N-периодической последовательности, а
X3 (n) – коэффициенты ДПФ 3N-периодической последовательности x (k ) .
Выразить X3 (n) через X (n) . Проверить результат для последовательности.
3. Пусть y(k) означает циклическую свёртку двух последовательностей x(k) и h(k),
0 ≤ k ≤ N −1. Проверить равенство
N −1
k = 0
⎛ N −1 ⎞⎛ N −1
⎞
⎝ k = 0 ⎠⎝ k = 0
⎠
∑ y(k) = ⎜ ∑ x(k) ⎟⎜ ∑ h(k) ⎟.
•••1
•••
k
–2 –1 0 1 2 3 4 5
2
1
1
1
2 2
2
N=