Процессы изменения состояния термодинамических систем

При изучении термодинамических процессов определяются:
1) закономерность изменения параметров состояния рабочего тела, то есть выводится уравнение процесса или дается его графическое изображение в координатах p-v, p-T, Т-s и т.д.;
2) параметры состояния системы в начальной и конечной точках процесса;
3) численные значения работы и теплообмена в процессе;
4) изменение значений внутренней энергии, энтальпии и энтропии рабочего тела.
Простейшие термодинамические процессы
Простейшими термодинамическими процессами обычно считают изобарный, изохорный и изопотенциальные процессы.

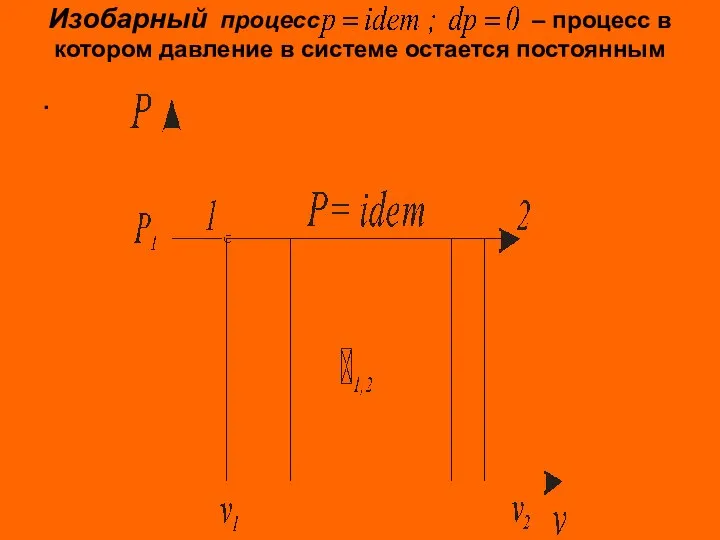
Изобарный процесс – процесс в котором давление в системе остается постоянным
.

Изобарные процессы подвода или отвода теплоты происходят в поршневых двигателях внутреннего сгорания, газотурбинных, паросиловых, холодильных установках и др.
Для идеального газа в изобарном процессе (1-2) соотношение объемов прямо пропорционально соотношению температур
Удельная термодинамическая и потенциальная работы в изобарном процессе определяются из соотношений

Для идеального газа
Количество теплоты, подведенной к рабочему телу или отведенной от него в изобарном процессе, опреде-ляется из выражения первого начала термодинамики
Для идеального газа

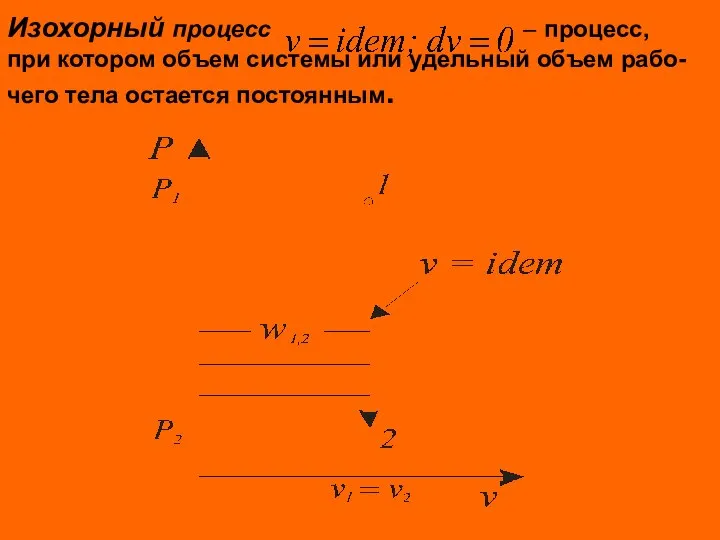
Изохорный процесс – процесс,
при котором объем системы или удельный объем рабо-
чего тела остается постоянным.

В изохорных процессах происходит увеличение
или уменьшение давления, что связано с соответствен –
ным изменением температуры – подводом или отводом
теплоты.
Изохорные процессы подвода или отвода теплоты
происходят в поршневых двигателях внутреннего сго-
рания, газотурбинных, паросиловых установках и др.
Для идеального газа в изохорном процессе соотношение давлений прямо пропорционально соотношению температур

Удельная термодинамическая и потенциальная
работы в изохорном процессе определяются из соотно-
шений
Для идеального газа
Количество теплоты, подведенной к рабочему телу
или отведенной от него в изохорном процессе, определя-
ется из выражения первого начала термодинамики

Для идеального газа
Изопотенциальный процесс – термодинамический
процесс изменения состояния системы, при котором
значение потенциальной функции сохраняет неизменное
значение

Для идеального газа, согласно уравнению Клапейрона
изопотенциальный процесс
является и изотермическим .
Удельная термодинамическая и потенциальная работы
в изопотенциальном процессе определяются из следую-
щих соотношений:

Нетрудно заметить, что постоянство
приводит к условию
Поэтому, в изопотенциальном процессе численные значения термодинамической и потенциальной работ равны между собой.

Для идеального газа pv=RT=idem (изотермический)
Количество теплоты, подведенной к рабочему телу или отведенной от него в изопотенциальном процессе определяется из выражения первого начала термодинамики по балансу рабочего тела
Для идеалного газа du=0; dh=0

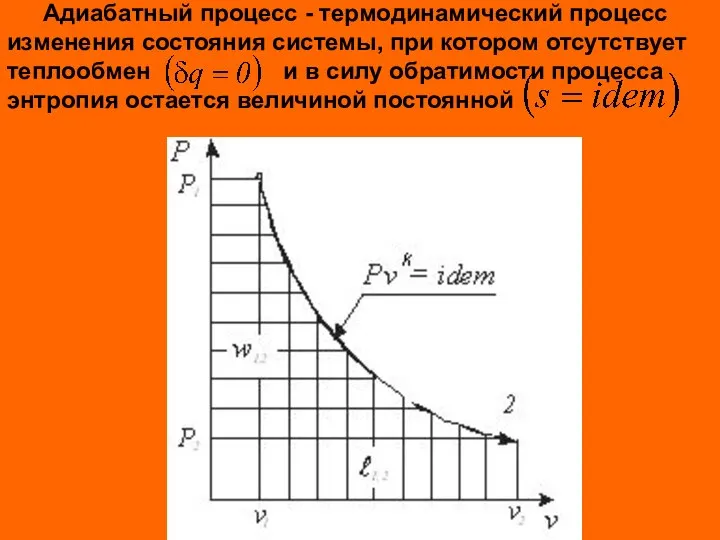
Адиабатный процесс - термодинамический процесс
изменения состояния системы, при котором отсутствует
теплообмен и в силу обратимости процесса
энтропия остается величиной постоянной

Из выражения первого начала термодинамики для
простого тела при условии имеем
Отсюда следует выражение для показателя адиабатного процесса
где ns=k – показатель адиабаты.
Расчетное выражение для расчета показателя адиабатного процесса

После интегрирования при условия постоянства
показателя процесса имеем
Для идеального газа показатель адиабаты равен
k= cp/cv

Из уравнения адиабатного процесса получим выражение для связи параметров состояния
потенцируя имеем

Выражения конечных (интегральных) величин
термодинамической и потенциальных работа в адиабат-
ном процесс можно получить при сопоставлении их
элементарных значений
С учетом определения показателя адиабаты имеем:

Интегрируя последнее выражение с учетом того, что k=idem, получим интегрального уравнения термодинамической работы
Введем понятие характеристики процесса расширения или сжатия

Окончательно имеем уравнения для определения термодинамической и потенциальной работы
Различные уравнения для определения характе-
ристики расширения или сжатия определяются с
учетом уравнения адиабаты

Применительно для идеального газа имеем:

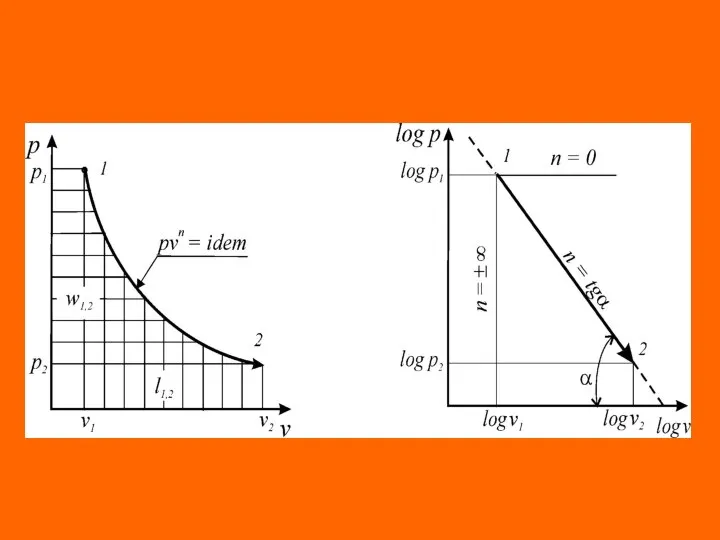
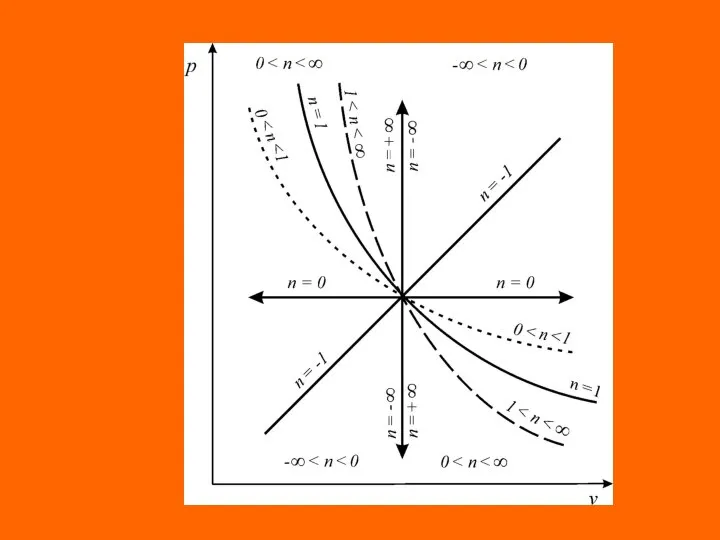
Уравнения перечисленных простейших и любых
других термодинамических процессов могут быть
представлены одним уравнением. Это уравнение назы-
вается уравнением политропы, а термодинамические
процессы, описываемые этим уравнением, называются
политропными.
Политропные процессы
Политропным процессом с постоянным показателем
называется обратимый термодинамический процесс
изменения состояния простого тела, подчиняющийся
уравнению

где п – показатель политропы, являющий в рассматриваемом процессе постоянной величиной, которая может иметь любые частные значения - положительные и отрицательные (-∞ ≤ n ≤ +∞).
Физический смысл показателя политропы п определяется после дифференцирования уравнения политропы

Это значит, что постоянный показатель
политропы определяется соотношением потенциальной
и термодинамической работ в элементарном или
конечном процессах. Значения этих работ могут быть
определены графически в координатах
В логарифмических координатах политропный
процесс (политропа) с постоянным показателем
представляет собой прямую линию
При этом, постоянный показатель политропы
определяется как тангенс угла наклона линии процесса к
оси абсцисс ( )

Из соотношения показателя политропи следует, что
для изобарного процесса , для изохорного процесса nv = ± ∞, для изопотенциальног процесса npv = 1 (для
идеального газа =1 , это означает, что для
идеального газа изоротенциальный, изотермический,
изоэнергетический и изоэнтальпийный процессы совпа
дают), для адиабатного процесс n = k.

Работа в политропных процессах
Выражения конечных (интегральных) величин
термодинамической и потенциальных работ в политро-
пных процессах
для идеального газа pv = RT и

Теплообмен в политропном процессе для простых тел выводится также на основе рассмотрения выражения первого начала термодинамики
Последнее выражение можно представить в виде
Удельная внутренняя энергия для простых тел может быть представлена в виде функции u =и (p, v).
Тогда дифференциал внутренней энергии запишется в следующем виде:

Введем следующие обозначения:
При этом выражение примет вид:
Подставив полученное уравнение в выражение первого начала термодинамики
получим

Для определения величин ( и ) рассмотрим два термодинамических процесса:
Изоэнергетический процесс (u = idem, du = 0 ,n = nu.)
Так как в изоэнергетическом процессе
Адиабатный процесс (δ q = 0). Для этого процесса
показатель политропы принимает значение n = k и элемен-
тарная термодинамическая работа также не равна нулю

С учетом полученных соотношений для определения av и
ap, находим выражения для расчета удельных значений
изменения внутренней энергии и теплообмена в элементарном
процессе:
Соотношения для расчета удельных значений изменения внутренней энергии и теплообмена в конечном процессе имеют следующий вид:
Для идеального газа nu = 1