Содержание
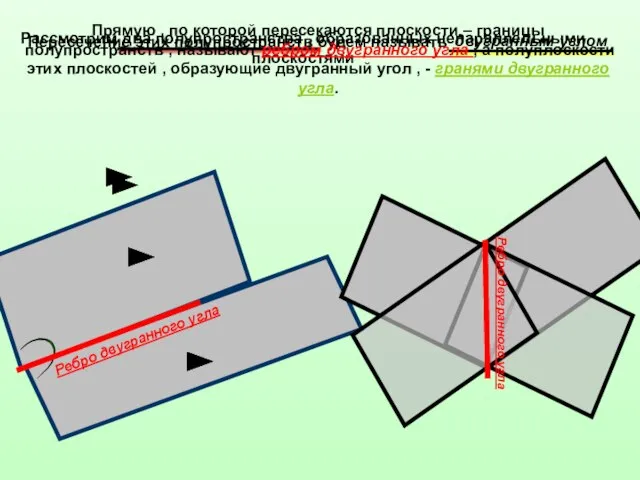
- 2. Рассмотрим два полупространства , образованных непараллельными плоскостями Пересечение этих полупространств будем называть двугранным углом Прямую ,
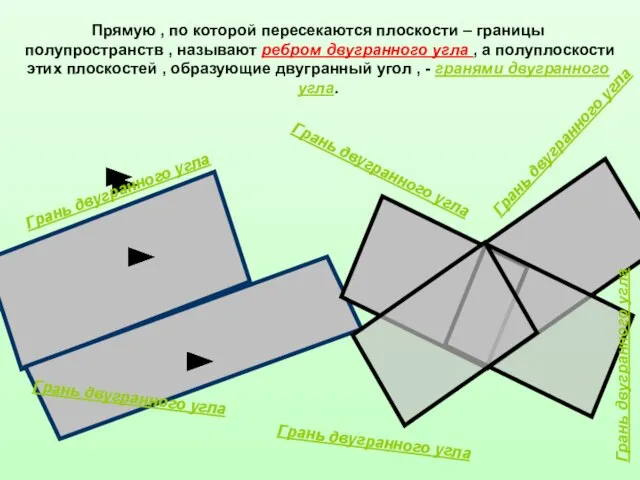
- 3. Прямую , по которой пересекаются плоскости – границы полупространств , называют ребром двугранного угла , а
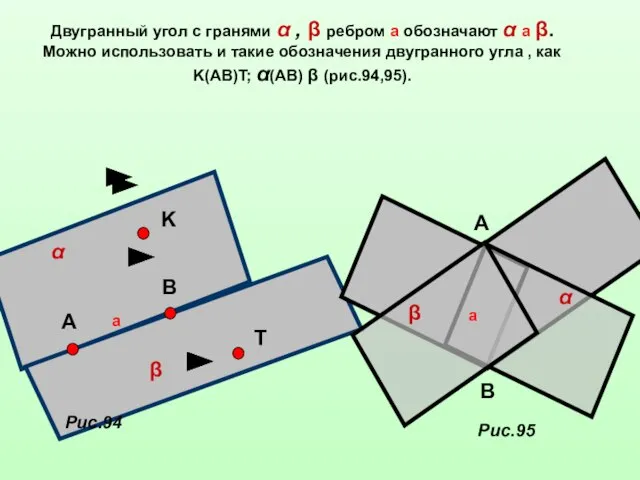
- 4. Двугранный угол с гранями α , β ребром а обозначают α а β. Можно использовать и
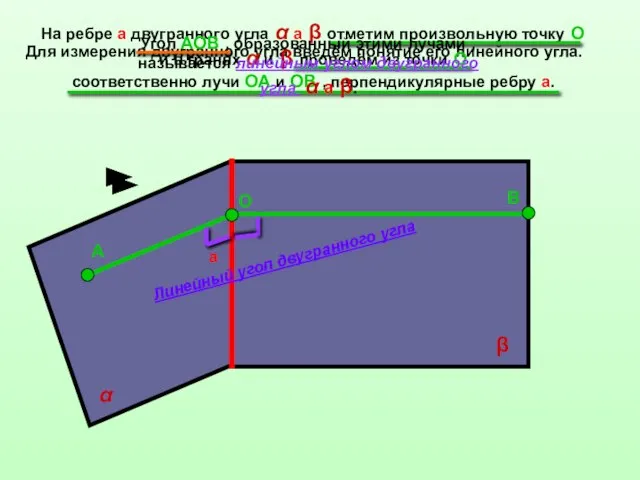
- 5. Для измерения двугранного угла введём понятие его линейного угла. На ребре а двугранного угла α а
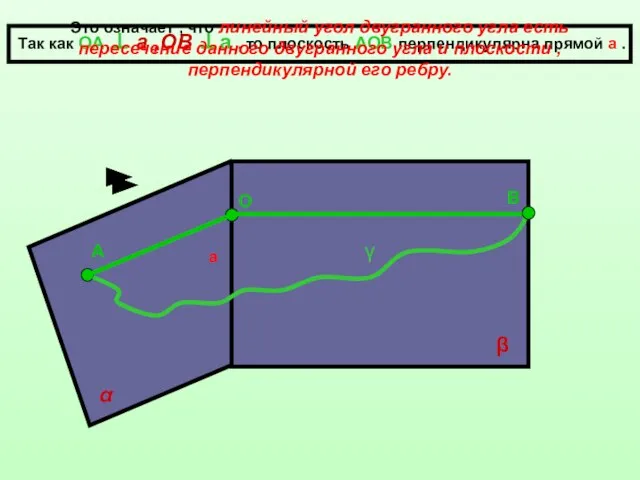
- 6. а α β О А В Так как ОА ⊥ а ,ОВ ⊥а , то плоскость
- 7. Теорема : Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. Определение
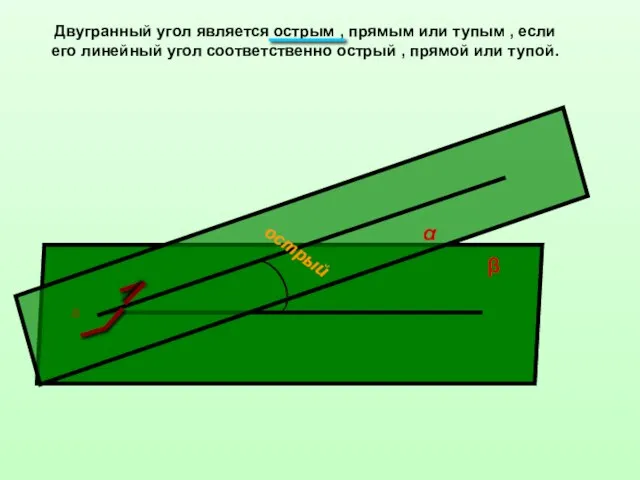
- 8. Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый ,
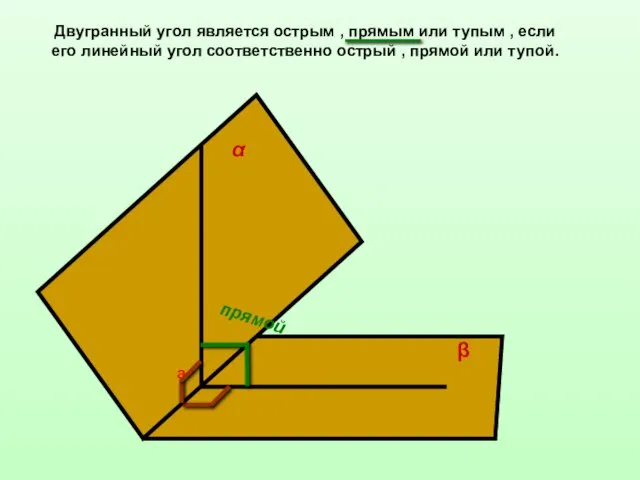
- 9. Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый ,
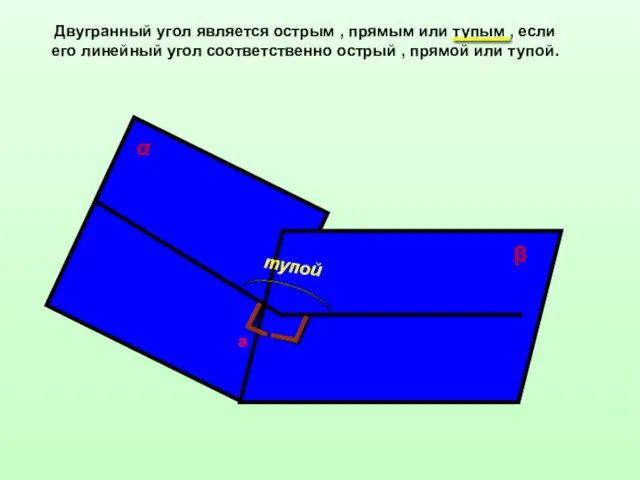
- 10. Двугранный угол является острым , прямым или тупым , если его линейный угол соответственно острый ,
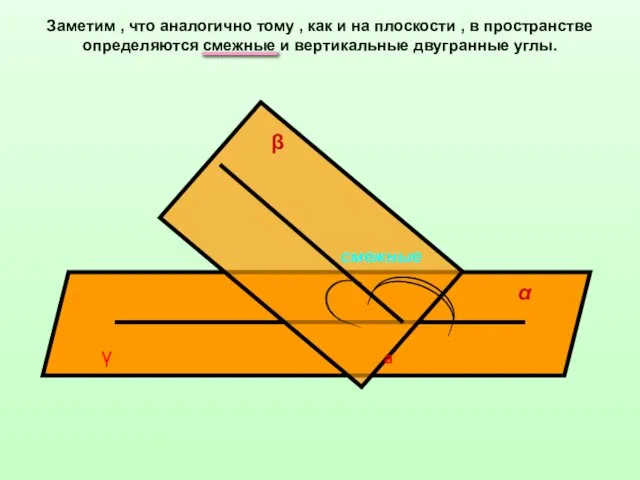
- 11. Заметим , что аналогично тому , как и на плоскости , в пространстве определяются смежные и
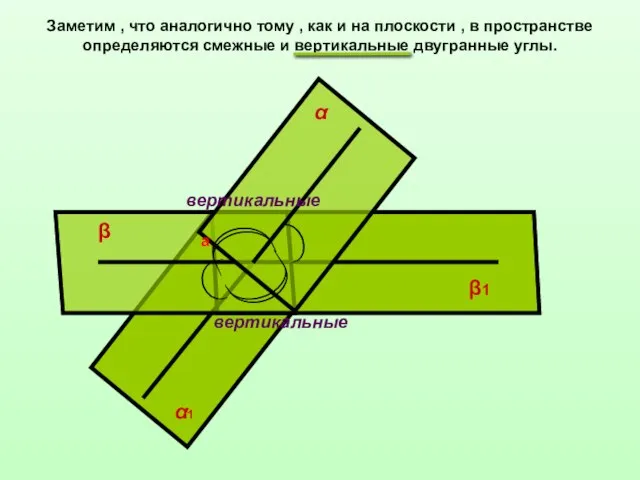
- 12. Заметим , что аналогично тому , как и на плоскости , в пространстве определяются смежные и
- 13. Определение : Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов , образованных при их
- 14. β β1 а α α1 с ϕ Величина угла между плоскостями принадлежит промежутку [0°;90°].
- 16. Скачать презентацию


![β β1 а α α1 с ϕ Величина угла между плоскостями принадлежит промежутку [0°;90°].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/485054/slide-13.jpg)
 Понятие многогранника
Понятие многогранника Путешествие в страну Геометрия
Путешествие в страну Геометрия Правильные многогранники
Правильные многогранники Цилиндр и конус
Цилиндр и конус Четырехугольники
Четырехугольники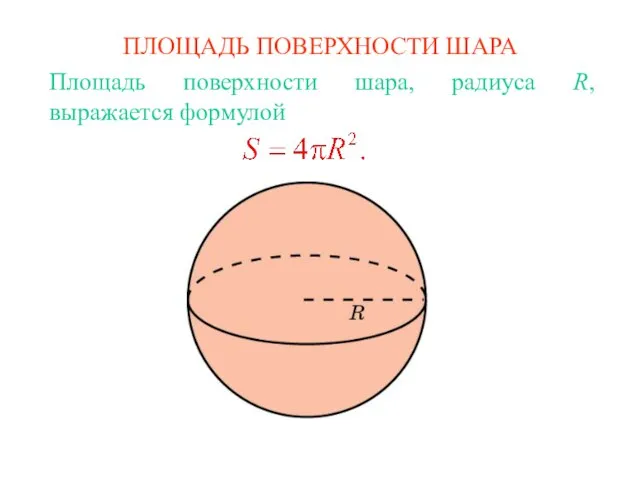 Площадь поверхности шара
Площадь поверхности шара Биссектриса угла
Биссектриса угла Расстояние между скрещивающимися прямыми
Расстояние между скрещивающимися прямыми Параллельный перенос 11 класс - презентация_
Параллельный перенос 11 класс - презентация_ вид разреза сечения
вид разреза сечения Плоскость
Плоскость Понятие объема. Объем призмы
Понятие объема. Объем призмы Теоремы синусов и косинусов
Теоремы синусов и косинусов Стереометрия в образах
Стереометрия в образах Тетраэдр и параллепипед
Тетраэдр и параллепипед Решение треугольников. Измерительные работы на местности
Решение треугольников. Измерительные работы на местности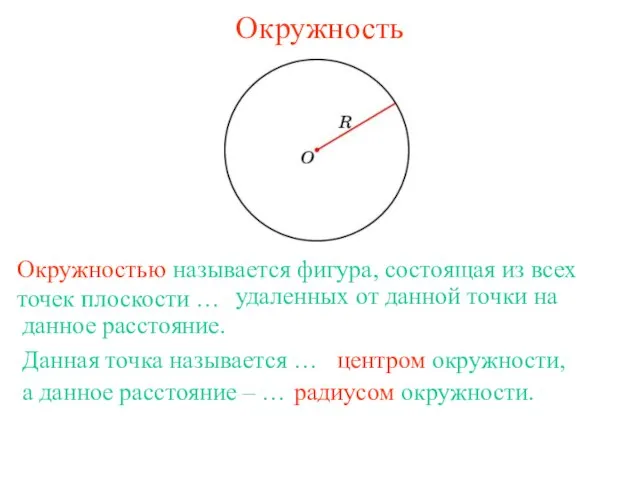 Окружность
Окружность Фракталы – геометрия природы
Фракталы – геометрия природы Многообразие многоугольников
Многообразие многоугольников Приготовьтесь к построению
Приготовьтесь к построению Окружность в аксонометрии
Окружность в аксонометрии Треугольники. Третий признак равенства
Треугольники. Третий признак равенства ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ
ЗАДАЧИ С ИНСТРУКЦИЕЙ ДЛЯ РЕШЕНИЯ ПО ТЕМЕ ОБЪЕМ ПИРАМИДЫ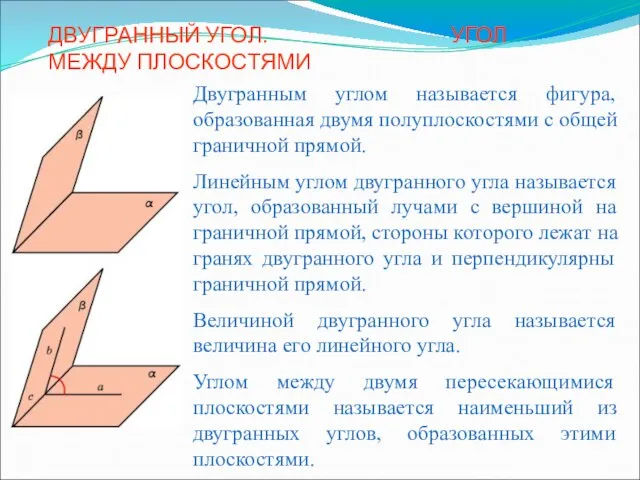 Двугранный угол. Угол между плоскостями4
Двугранный угол. Угол между плоскостями4 Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе)
Соотношения между сторонами и углами прямоугольного треугольника (Подготовка к контрольной работе) Урок повторения в 6 классе
Урок повторения в 6 классе В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Симметрия на планете Земля
Симметрия на планете Земля