Слайд 2Великий и непредсказуемый
Пифагор.

Слайд 3Карл Гаусс, учащийся первого курса Геттингенского университета, решил задачу, перед которой математическая

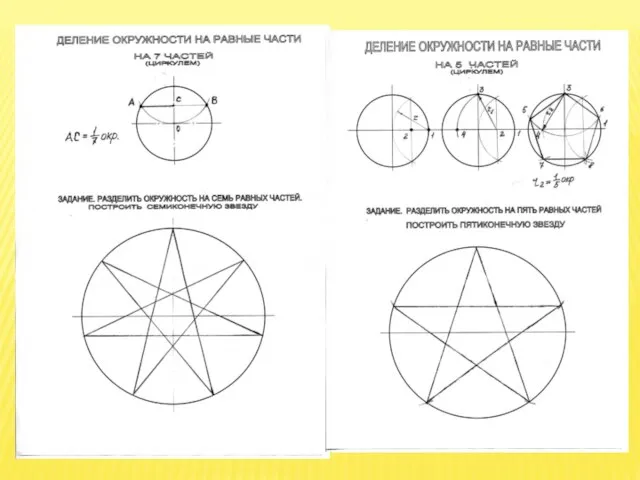
наука пасовала более двух с лишним тысяч лет. Несмотря на то, что еще древними греками были найдены способы построения с помощью только лишь циркуля и линейки правильных многоугольников с числом сторон 3, 4, 5, 15, а также с числом сторон, большим в 2 раза, в отношении прочих правильных многоугольников царила полная неизвестность.
И вот именно в этот день 1796 года будущий «король математиков» Гаусс догадался, как построить правильный 17-угольник, кстати, также, с помощью циркуля и линейки. Это открытие стало поворотным пунктом в его жизни: ранее колебавшийся между филологией и математикой, теперь он твердо решил посвятить себя последней. Кстати, он завещал изобразить 17-угольник на своем надгробии – что и было сделано.
Слайд 11
В природе, в окружающем мире, в быту - всюду мы видим правильные

многоугольники
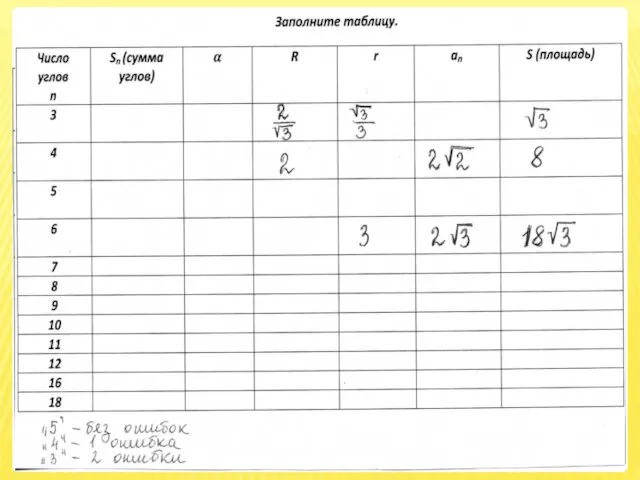
Слайд 12ДЕЛЕНИЕ НА ЧЕТЫРЕ РАВНЫЕ ЧАСТИ
.

















 Пентагон
Пентагон Признаки параллельности прямых
Признаки параллельности прямых Фракталы и их применение в наши дни
Фракталы и их применение в наши дни Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс
Изображение пространственных фигур Мячина Екатерина Колдаева Есения 11 Г класс Геометрия
Геометрия Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Периметр. Площа - презентация по Геометрии_
Периметр. Площа - презентация по Геометрии_ Бумажные складные модели и их использование на уроках геометрии в 10 классе
Бумажные складные модели и их использование на уроках геометрии в 10 классе Площади комбинированных фигур
Площади комбинированных фигур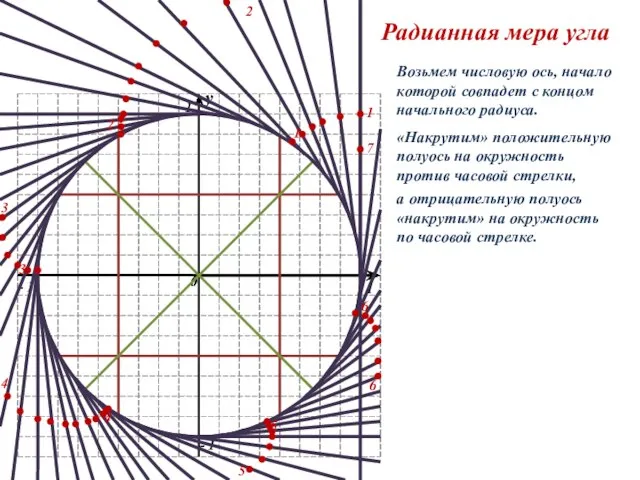 Радианная мера угла
Радианная мера угла Разные способы нахождения площади многоугольников
Разные способы нахождения площади многоугольников ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ
ПИФАГОРОВЫ ШТАНЫ НА ВСЕ СТОРОНЫ РАВНЫ Резьба. Крепёжные изделия
Резьба. Крепёжные изделия Уравнения, содержащие обратные тригонометрические функции
Уравнения, содержащие обратные тригонометрические функции Анализ геометрической формы предмета
Анализ геометрической формы предмета Лист Мёбиуса
Лист Мёбиуса ЭЛЛИПС
ЭЛЛИПС Скалярное произведение векторов
Скалярное произведение векторов Теорема о вписанном угле 8 класс - презентация_
Теорема о вписанном угле 8 класс - презентация_ Средняя линия треугольника 8 класс
Средняя линия треугольника 8 класс Развёртка куба
Развёртка куба «Чтение графиков. ЕГЭ» ЮВАО
«Чтение графиков. ЕГЭ» ЮВАО Проецирование точки на три плоскости
Проецирование точки на три плоскости Перпендикулярность прямой и плоскости
Перпендикулярность прямой и плоскости Площади
Площади ТЕСТ по теме «Параллельные прямые»
ТЕСТ по теме «Параллельные прямые» Смежные и вертикальные углы
Смежные и вертикальные углы Геометрические построения на плоскости
Геометрические построения на плоскости