Содержание
- 2. Цели: Систематизация и обобщение приемов работы с пространственными объектами: прямыми , плоскостями и телами Знакомство с
- 3. Задачи: Устная работа по актуализация необходимых известных приемов работы с пространственными объектами: прямыми и плоскостями Определение
- 4. Средства: Модели пространственных фигур, чертежи к задачам Теорема Фалеса и теорема о трех перпендикулярах Приемы стерео
- 5. План: Первый урок: Актуализация: выполнение устных заданий, доказательство теоремы, решение задачи Определение и усвоение нового понятия
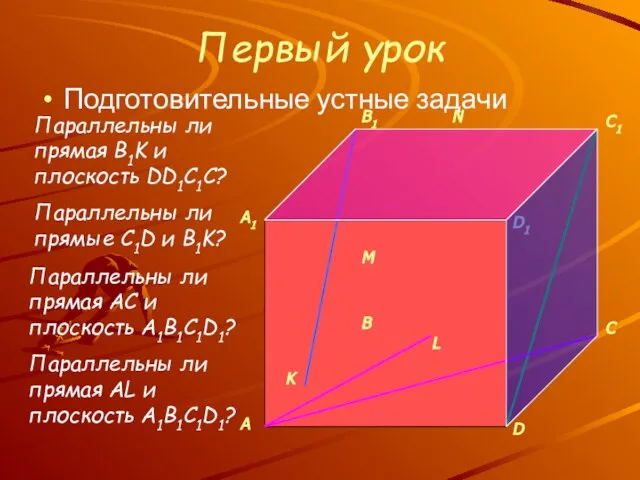
- 6. Первый урок Подготовительные устные задачи M K L N Параллельны ли прямая B1K и плоскость DD1C1C?
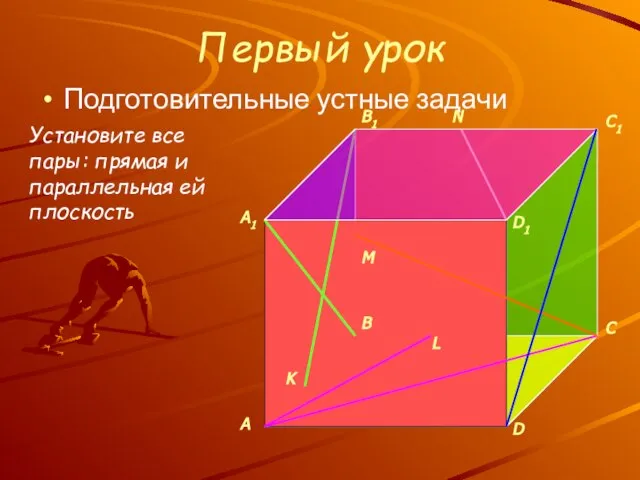
- 7. Первый урок Подготовительные устные задачи M K L N Установите все пары: прямая и параллельная ей
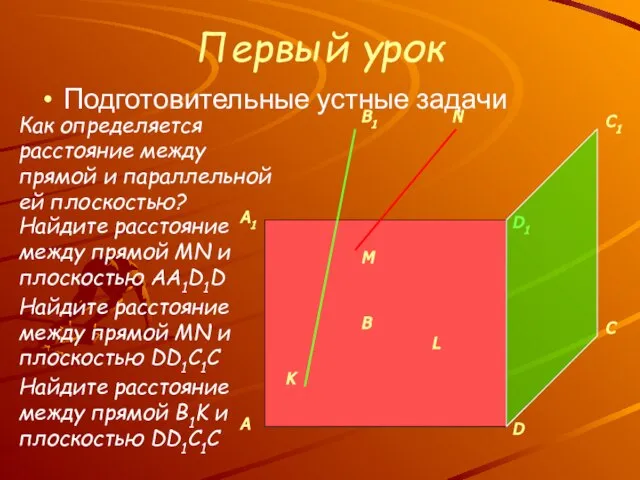
- 8. Первый урок Подготовительные устные задачи M K L N Как определяется расстояние между прямой и параллельной
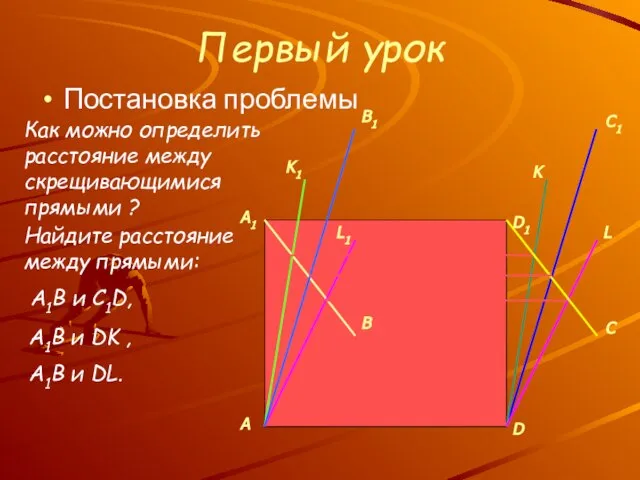
- 9. Первый урок Постановка проблемы K L Как можно определить расстояние между скрещивающимися прямыми ? K1 L1
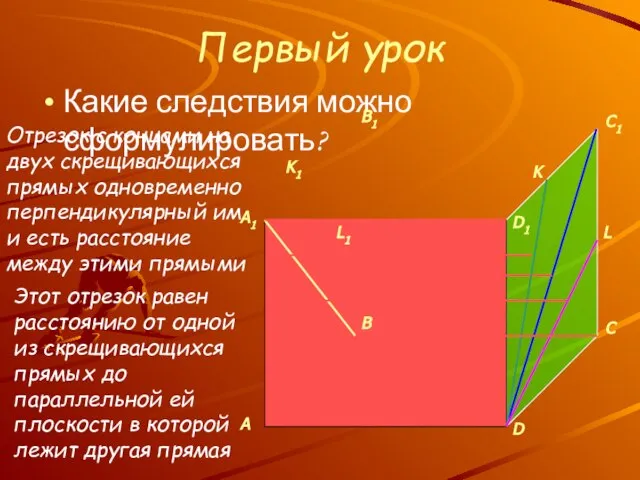
- 10. Первый урок Какие следствия можно сформулировать? K L Отрезок с концами на двух скрещивающихся прямых одновременно
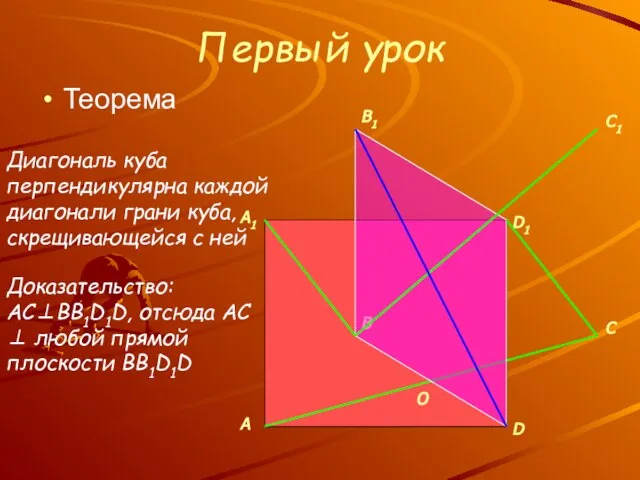
- 11. Первый урок Теорема O Диагональ куба перпендикулярна каждой диагонали грани куба, скрещивающейся с ней Доказательство: AC⊥BB1D1D,
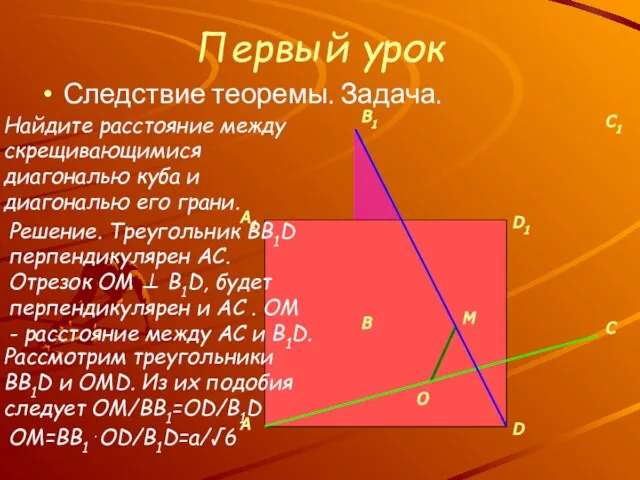
- 12. Первый урок Следствие теоремы. Задача. O M Рассмотрим треугольники BB1D и OMD. Из их подобия следует
- 13. Второй урок Обобщение.Три типовых случая определения расстояния между скрещивающимися прямыми Общий перпендикуляр к обеим прямым (единственный!)
- 14. Второй урок Проблема: Как найти плоскость с одной прямой, параллельную другой скрещивающейся прямой ? Достаточно провести
- 15. Второй урок Типовые задачи Чаще других возникают задачи с перпендикулярными скрещивающимися прямыми. К этому типу относится
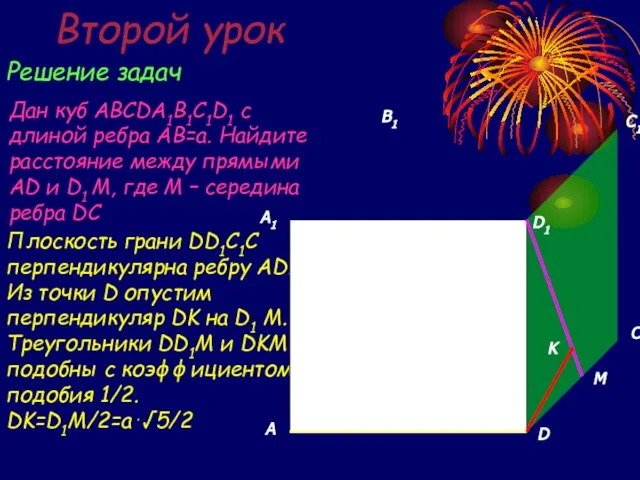
- 16. Второй урок Решение задач Дан куб ABCDA1B1C1D1 с длиной ребра AB=a. Найдите расстояние между прямыми AD
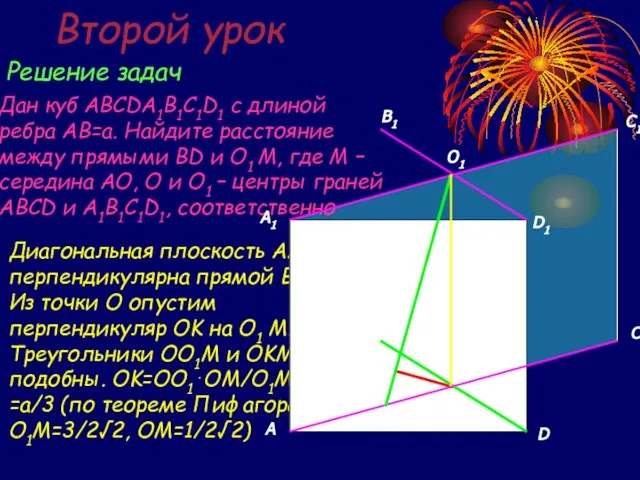
- 17. Второй урок Решение задач Дан куб ABCDA1B1C1D1 с длиной ребра AB=a. Найдите расстояние между прямыми BD
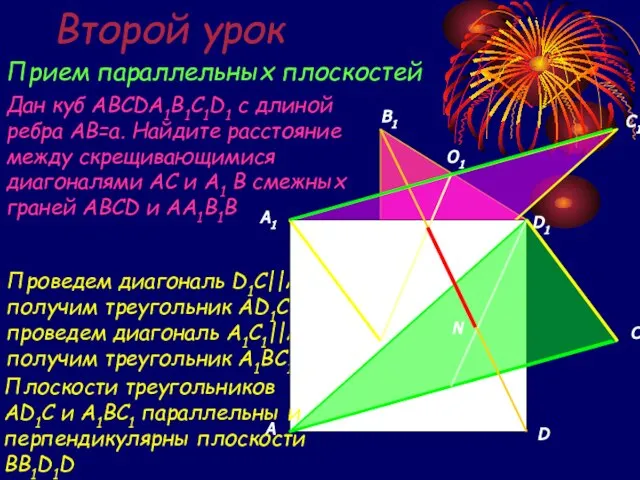
- 18. Второй урок Прием параллельных плоскостей Дан куб ABCDA1B1C1D1 с длиной ребра AB=a. Найдите расстояние между скрещивающимися
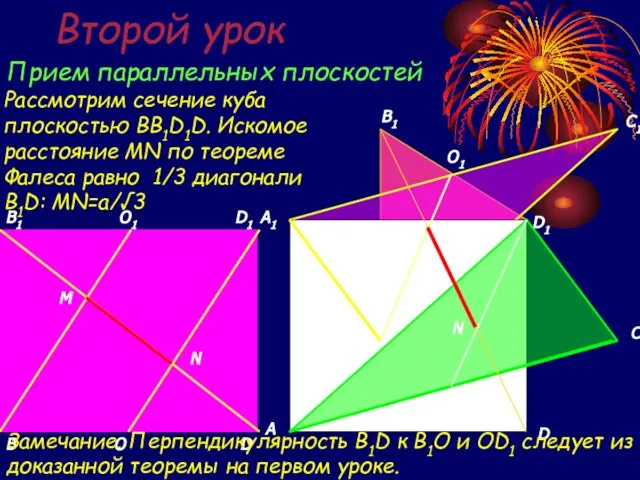
- 19. Второй урок Прием параллельных плоскостей O1 K M O M N Рассмотрим сечение куба плоскостью BB1D1D.
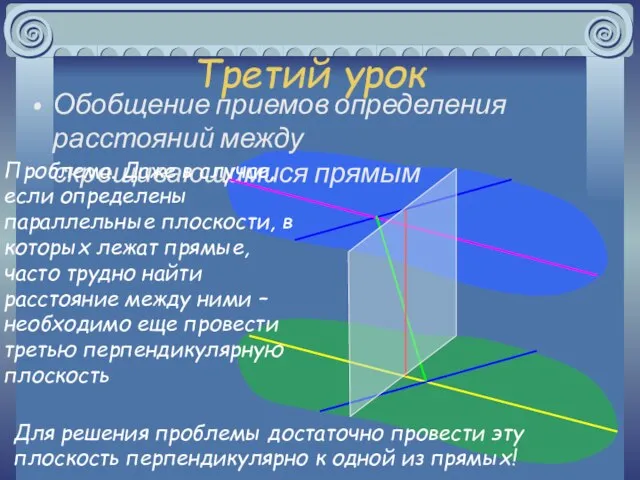
- 20. Третий урок Обобщение приемов определения расстояний между скрещивающимися прямым Проблема. Даже в случае, если определены параллельные
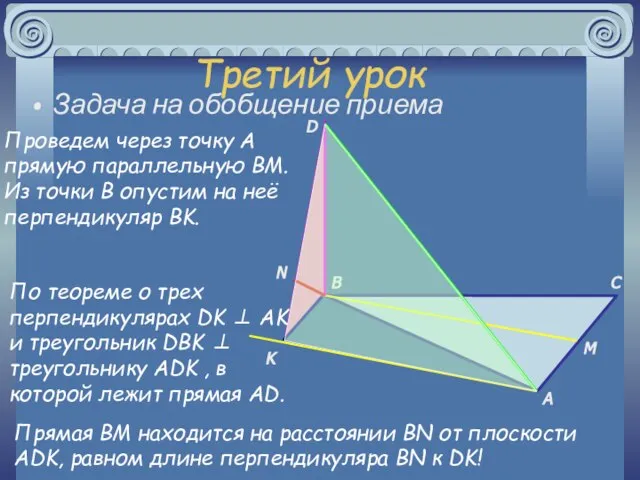
- 21. Третий урок Задача на обобщение приема Проведем через точку A прямую параллельную BM. Из точки B
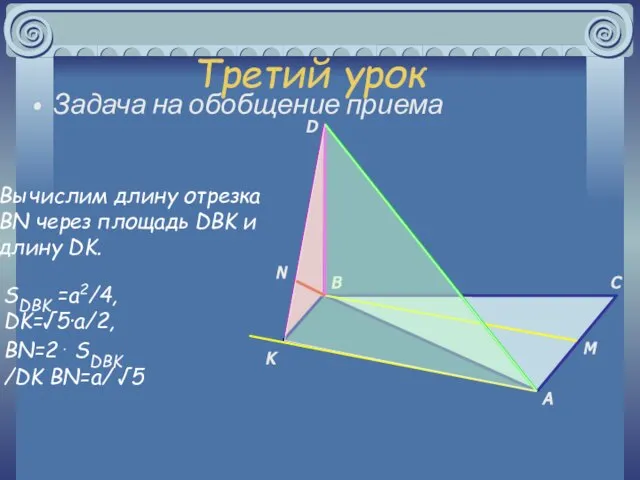
- 22. Третий урок Задача на обобщение приема A B C M D K N Вычислим длину отрезка
- 23. Третий урок Рефлексия. Осмысление обобщенного приема Рассмотренный способ последней задачи носит обобщенный характер. Если не проходят
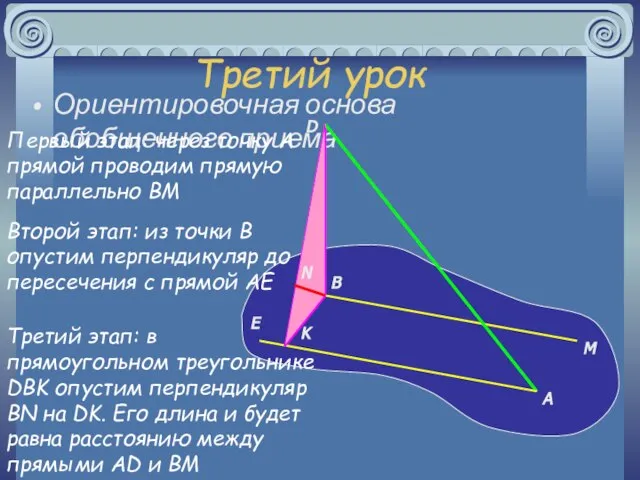
- 24. Третий урок Ориентировочная основа обобщенного приема Первый этап: через точку A прямой проводим прямую параллельно BM
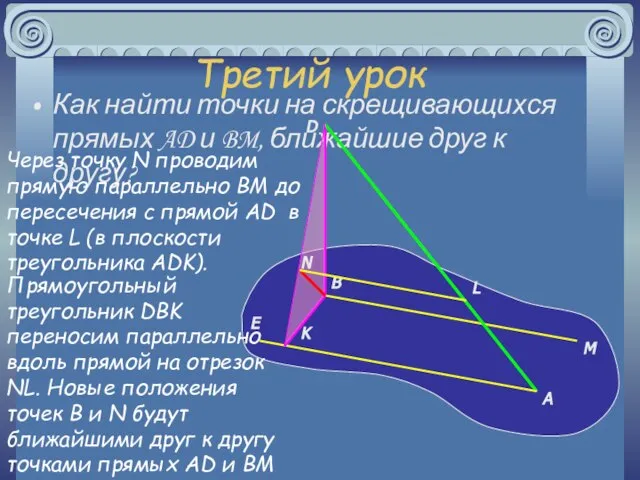
- 25. Третий урок Как найти точки на скрещивающихся прямых AD и BM, ближайшие друг к другу? Через
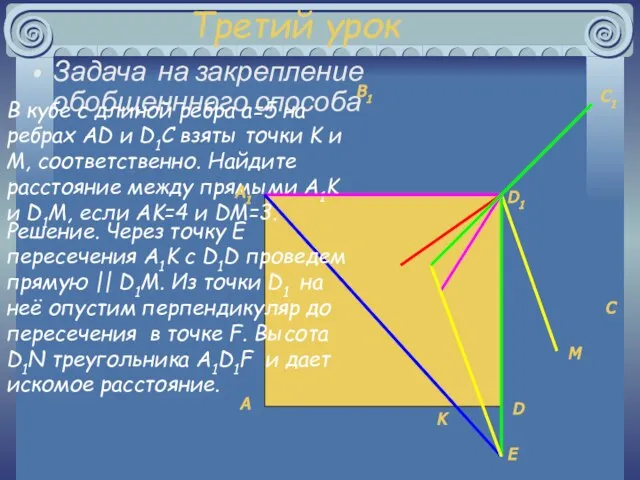
- 26. Третий урок Задача на закрепление обобщеннного способа В кубе с длиной ребра a=5 на ребрах AD
- 28. Скачать презентацию








 Геометрия в древние и новые века
Геометрия в древние и новые века Смежные и вертикальные углы
Смежные и вертикальные углы Фракталы – геометрия природы
Фракталы – геометрия природы Геометрические фигуры (Взаимное расположение на плоскости)
Геометрические фигуры (Взаимное расположение на плоскости) Амидекстр
Амидекстр Магические квадраты (5 класс)
Магические квадраты (5 класс) Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год.
Учитель математики МОУ СОШ № 4 им. Б. Машука г.Завитинска Амурской области. 2010-2011 уч. год. Проецирование точки на три плоскости
Проецирование точки на три плоскости Циклоида
Циклоида Умножение вектора на число
Умножение вектора на число Угол между плоскостями
Угол между плоскостями Геометрия крестово-купольного храма
Геометрия крестово-купольного храма Решение задач по геометрии на готовых чертежах
Решение задач по геометрии на готовых чертежах Доклад о «Сфере и шаре»
Доклад о «Сфере и шаре» Свойство и признак описанного четырёхугольника
Свойство и признак описанного четырёхугольника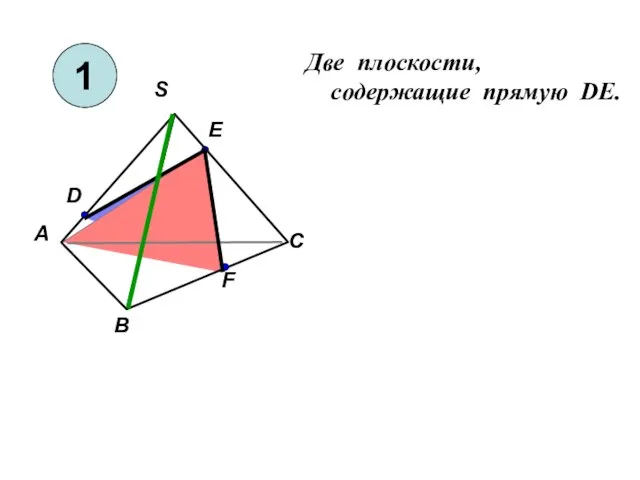 Две плоскости, cодержащие прямую DE
Две плоскости, cодержащие прямую DE Скалярное произведение векторов
Скалярное произведение векторов Взаимное расположение прямых в пространстве
Взаимное расположение прямых в пространстве Смежные и вертикальные углы
Смежные и вертикальные углы Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Установление соотношения между сторонами и углами прямоугольного треугольника
Установление соотношения между сторонами и углами прямоугольного треугольника Презентацию выполнила учитель ГБОУ СОШ №72 Андреева И.Ю.
Презентацию выполнила учитель ГБОУ СОШ №72 Андреева И.Ю. Координаты на плоскости
Координаты на плоскости Тема урока: УГОЛ Цель урока: сформировать полное представление о угле как геометрическом понятии
Тема урока: УГОЛ Цель урока: сформировать полное представление о угле как геометрическом понятии Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним
Внешний угол произвольного треугольника больше каждого внутреннего, не смежного с ним Признаки равенства и подобия треугольников
Признаки равенства и подобия треугольников Треугольники 3 класс
Треугольники 3 класс