Понятие объема. Объем призмы

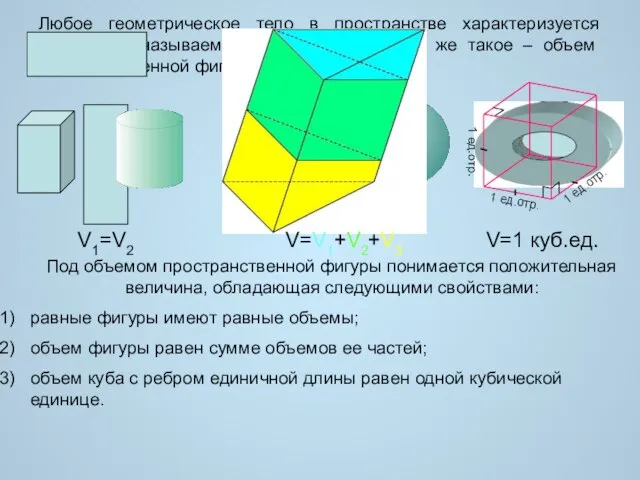
Любое геометрическое тело в пространстве характеризуется величиной, называемой ОБЪЕМОМ. Так что же такое – объем пространственной фигуры?
Под объемом пространственной фигуры понимается положительная величина, обладающая следующими свойствами:
равные фигуры имеют равные объемы;
объем фигуры равен сумме объемов ее частей;
объем куба с ребром единичной длины равен одной кубической единице.
V1=V2
V=V1+V2+V3
V=1 куб.ед.

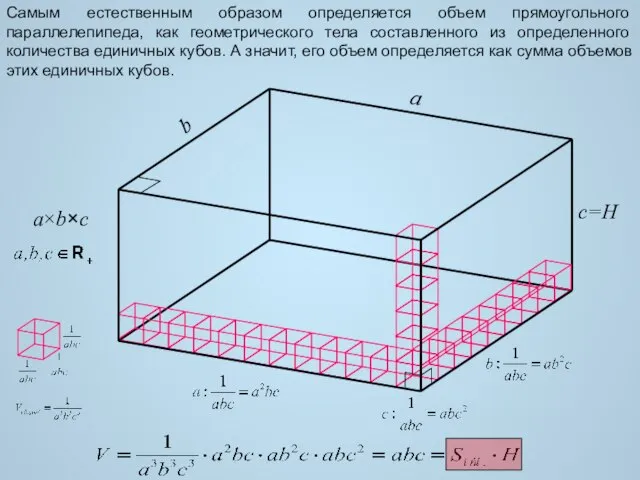
a
b
c=H
a×b×c
Самым естественным образом определяется объем прямоугольного параллелепипеда, как геометрического тела составленного из определенного количества единичных кубов. А значит, его объем определяется как сумма объемов этих единичных кубов.

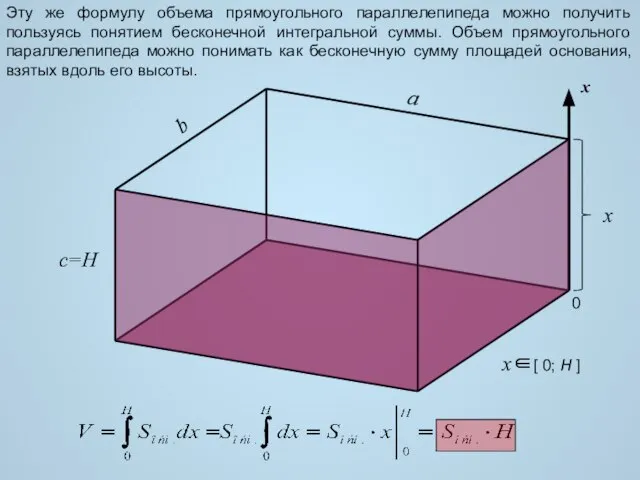
a
b
c=H
Эту же формулу объема прямоугольного параллелепипеда можно получить пользуясь понятием бесконечной интегральной суммы. Объем прямоугольного параллелепипеда можно понимать как бесконечную сумму площадей основания, взятых вдоль его высоты.
x
0
x
x∈[ 0; H ]

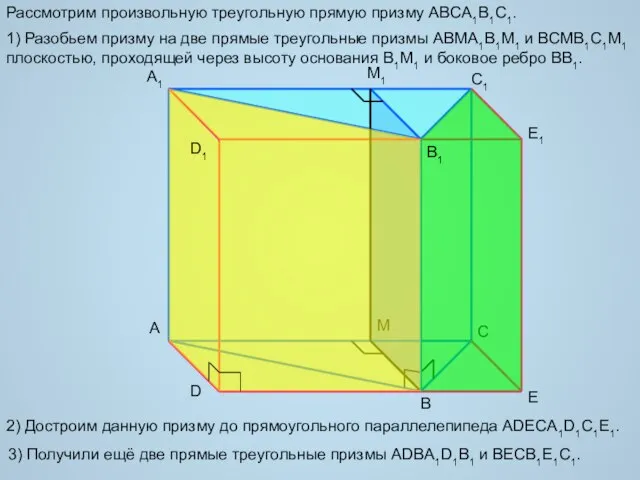
A
B
A1
C1
E1
D
E
M
M1
Рассмотрим произвольную треугольную прямую призму ABCA1B1C1.
1) Разобьем призму на две прямые треугольные призмы ABMA1B1M1 и BCMB1C1M1 плоскостью, проходящей через высоту основания B1M1 и боковое ребро BB1.
2) Достроим данную призму до прямоугольного параллелепипеда ADECA1D1C1E1.
C
3) Получили ещё две прямые треугольные призмы ADBA1D1B1 и BECB1E1C1.
D1
B1

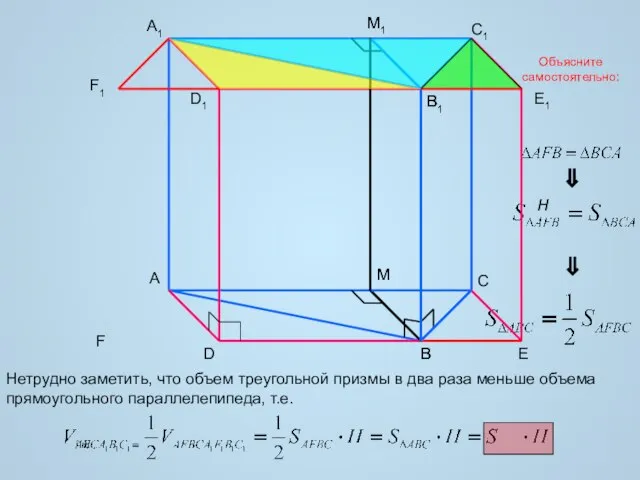
A
B
C
A1
B1
C1
D1
E1
D
E
M
M1
Нетрудно заметить, что объем треугольной призмы в два раза меньше объема прямоугольного параллелепипеда, т.е.
H
⇒
B1
B
M1
M
⇒
Объясните самостоятельно:
F1
F

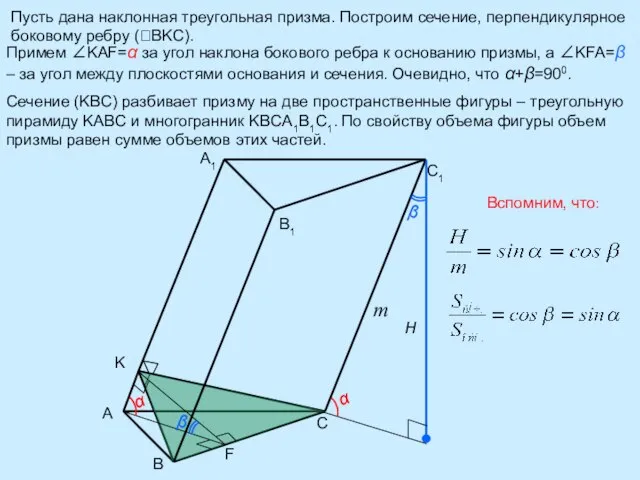
Пусть дана наклонная треугольная призма. Построим сечение, перпендикулярное боковому ребру (BKC).
A
B
C
K
A1
B1
C1
α
β
F
Примем ∠KAF=α за угол наклона бокового ребра к основанию призмы, а ∠KFA=β – за угол между плоскостями основания и сечения. Очевидно, что α+β=900.
Сечение (KBC) разбивает призму на две пространственные фигуры – треугольную пирамиду KABC и многогранник KBCA1B1C1. По свойству объема фигуры объем призмы равен сумме объемов этих частей.
Вспомним, что:
α
H
m
β

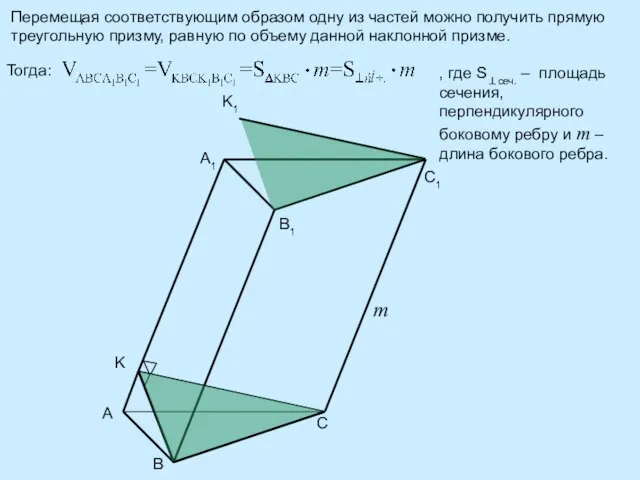
Перемещая соответствующим образом одну из частей можно получить прямую треугольную призму, равную по объему данной наклонной призме.
B
C
K
A1
B1
C1
A
K1
m
Тогда:
, где S⊥сеч. – площадь сечения, перпендикулярного боковому ребру и m –длина бокового ребра.

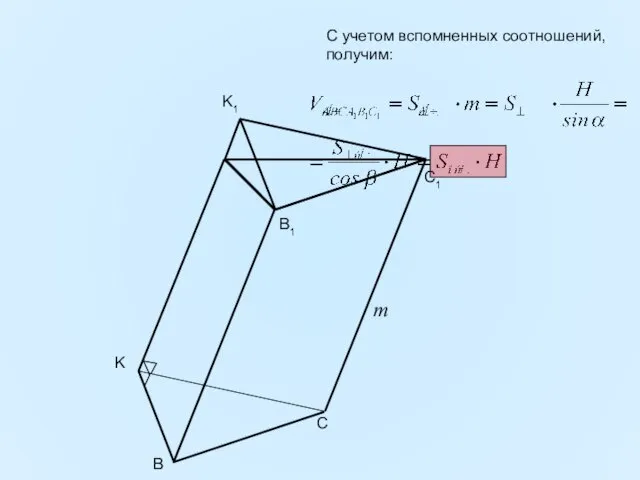
С учетом вспомненных соотношений, получим:
B
C
K
B1
C1
K1
m

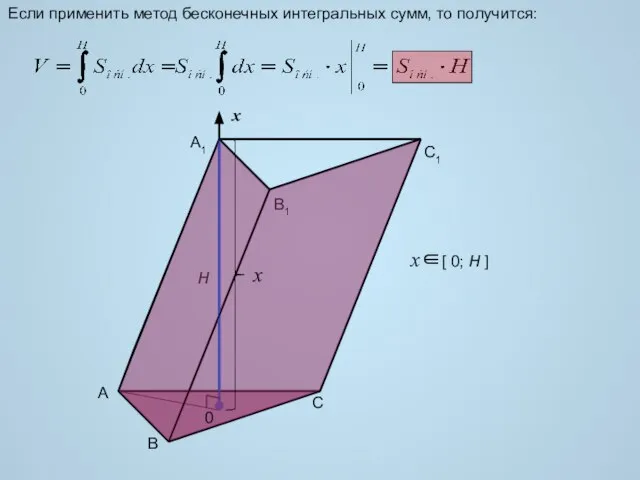
A
B
C
B1
H
A1
C1
Если применить метод бесконечных интегральных сумм, то получится:
x
x
x∈[ 0; H ]
0

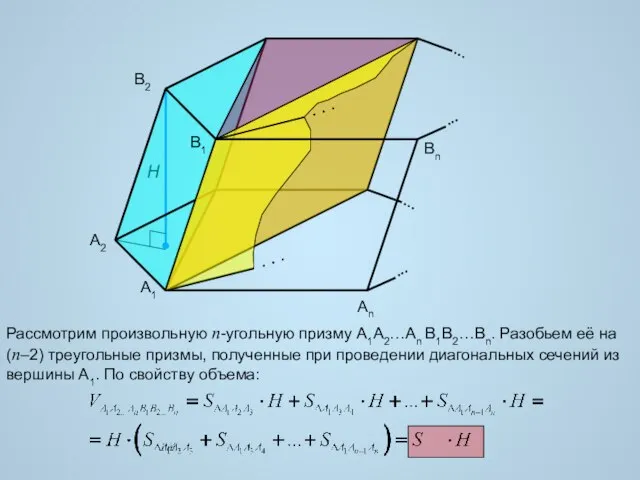
H
Рассмотрим произвольную n-угольную призму A1A2…An B1B2…Bn. Разобьем её на (n–2) треугольные призмы, полученные при проведении диагональных сечений из вершины A1. По свойству объема:
A1
A2
An
B1
B2
Bn