Четырехугольники

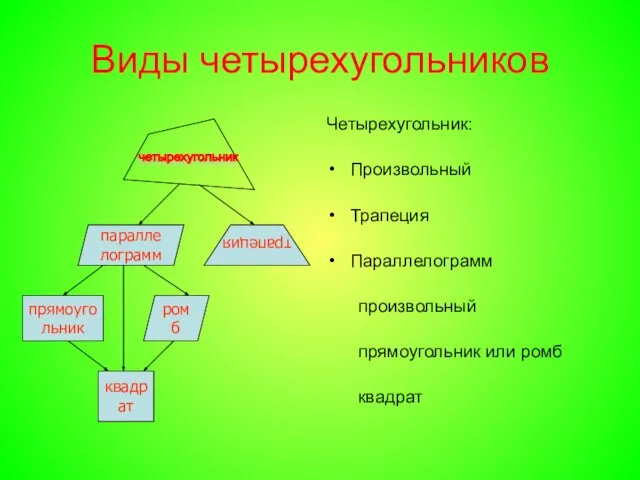
Виды четырехугольников
Четырехугольник:
Произвольный
Трапеция
Параллелограмм
произвольный
прямоугольник или ромб
квадрат

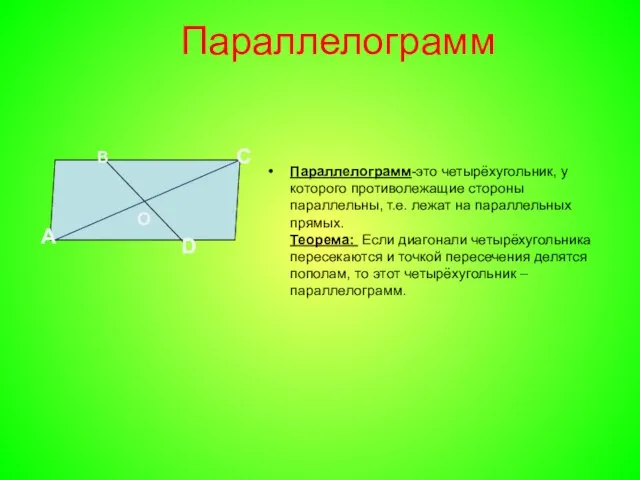
Параллелограмм
Параллелограмм-это четырёхугольник, у которого противолежащие стороны параллельны, т.е. лежат на параллельных прямых.
Теорема: Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник –параллелограмм.
В
А
С
D
O

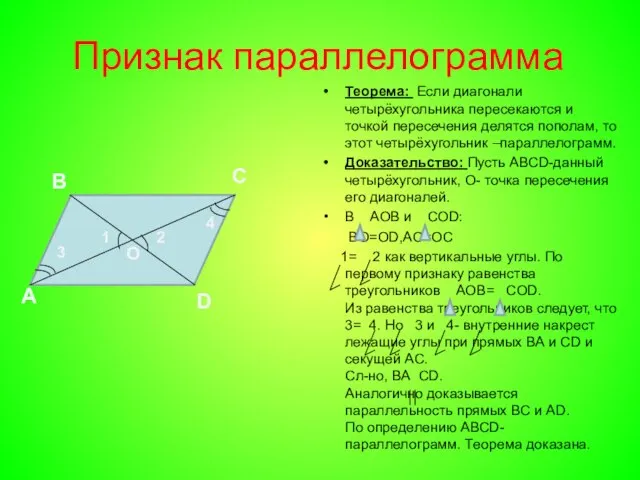
Признак параллелограмма
Теорема: Если диагонали четырёхугольника пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник –параллелограмм.
Доказательство: Пусть АВСD-данный четырёхугольник, О- точка пересечения его диагоналей.
В АОВ и СОD:
BO=OD,AO=OС
1= 2 как вертикальные углы. По первому признаку равенства треугольников AOB= COD. Из равенства треугольников следует, что 3= 4. Но 3 и 4- внутренние накрест лежащие углы при прямых ВА и СD и секущей АС. Сл-но, ВА CD. Аналогично доказывается параллельность прямых ВС и АD. По определению АВСD-параллелограмм. Теорема доказана.
В
С
D
O
1
2
3
4
А

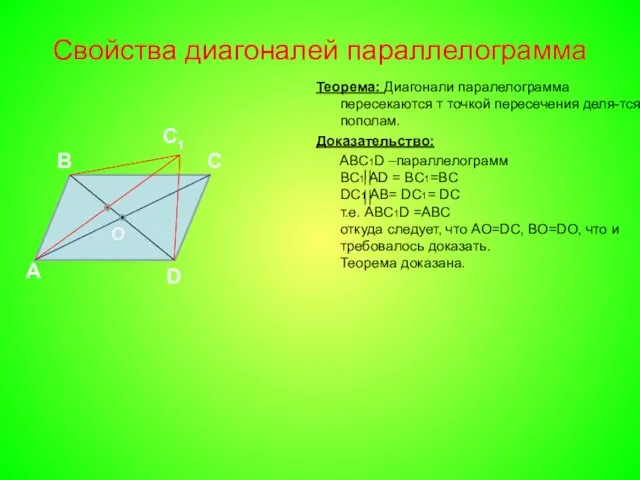
Свойства диагоналей параллелограмма
Теорема: Диагонали паралелограмма пересекаются т точкой пересечения деля-тся пополам.
Доказательство: АВС1D –параллелограмм ВС1 АD = BС1=BС DС1 АВ= DС1= DС т.е. АВС1D =АВС откуда следует, что АО=DС, ВО=DО, что и требовалось доказать. Теорема доказана.
В
С
А
D
O
С
1

ПРЯМОУГОЛЬНИК
Определение: Прямоугольник- это параллелограмм, к которого все углы прямые. Теорема: Диагонали прямоугольника равны.
С
В
А
D

ПРИЗНАК ПРЯМОУГОЛЬНИКА
Теорема: Диагонали прямоугольника равны.
Доказательство: Пусть АВС D– данный прямоугольник. Утверждение теоремы следует из равенства прямоугольных треугольников ВАD и СD А. У них углы ВАD и СDА прямые. Катет АD общий, А катеты АВ и СD равны как противолежащие стороны параллелограмма. Из равенства треугольников следует, что их гипотенузы равны. А гипотенузы есть диагонали прямоугольника. Теорема доказана.
С
В
А
D

РОМБ
Определение: Ромб- это параллелограмм, у которого все стороны равны.
Теорема: Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисой его углов.
А
В
С
D

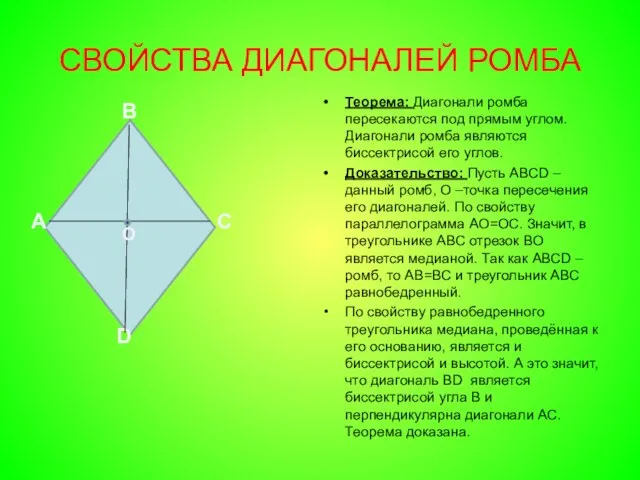
СВОЙСТВА ДИАГОНАЛЕЙ РОМБА
Теорема: Диагонали ромба пересекаются под прямым углом. Диагонали ромба являются биссектрисой его углов.
Доказательство: Пусть АВСD – данный ромб, О –точка пересечения его диагоналей. По свойству параллелограмма АО=ОС. Значит, в треугольнике АВС отрезок ВО является медианой. Так как АВСD – ромб, то АВ=ВС и треугольник АВС равнобедренный.
По свойству равнобедренного треугольника медиана, проведённая к его основанию, является и биссектрисой и высотой. А это значит, что диагональ ВD является биссектрисой угла В и перпендикулярна диагонали АС. Теорема доказана.
С
D
А
В
O