Объём призмы

ОБЪЁМ ПРИЗМЫ.
ПЛАН ТЕМЫ:
I. Понятие объема.
II. Основные свойства объёмов.
III. Объём произвольной призмы.

Объем каждого тела выражается положительным числом, которое показывает, сколько единиц измерения объемов и частей единицы содержится в данном теле.
Понятие объема

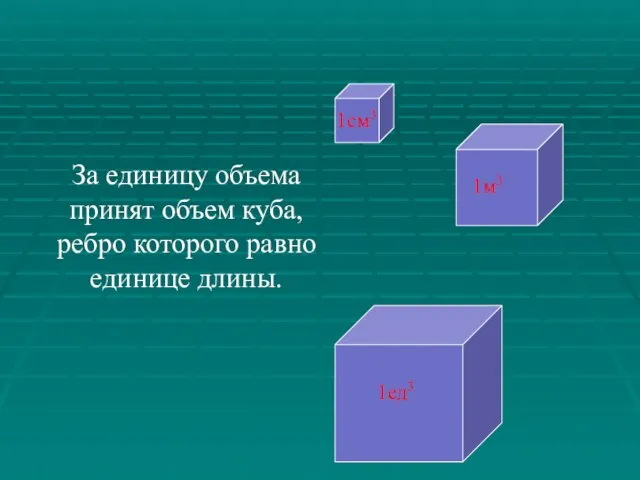
За единицу объема принят объем куба, ребро которого равно единице длины.
1см3
1м3
1ед3

Чтобы найти объём многогранника, нужно разбить его на кубы с ребром, равным единице измерения.
V=12ед.3

Общие свойства объемов тел:
I. Равные тела имеют равные объемы, при перемещении тела его объем не изменяется.
II. Если тело разбить на части, являющиеся простыми телами, то объем тела равен сумме объемов этих частей.

Равные тела имеют равные объемы, при перемещении тела его объем не изменяется;
Рассмотрим первое свойство.
V1
V2
V1= V2

Рассмотрим второе свойство.
Если тело разбить на части, являющиеся простыми телами, то объем тела равен сумме объемов всех частей.

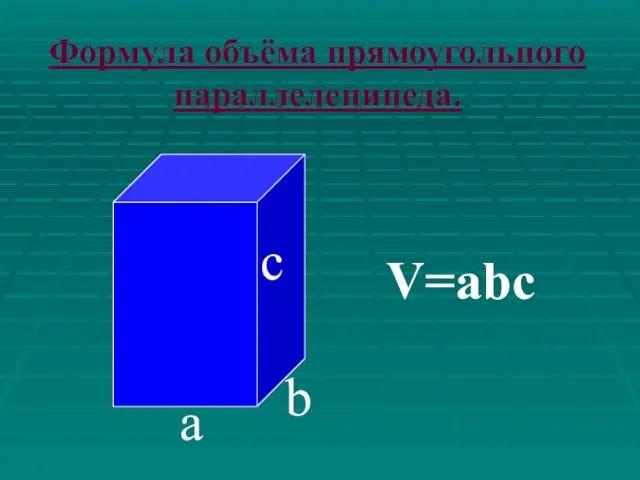
с
а
b
V=abc
Формула объёма прямоугольного параллелепипеда.

Объем прямой треугольной призмы, в основании которой лежит прямоугольный треугольник, равен произведению площади основания на высоту.
V=abc
V=abc
:2
:2

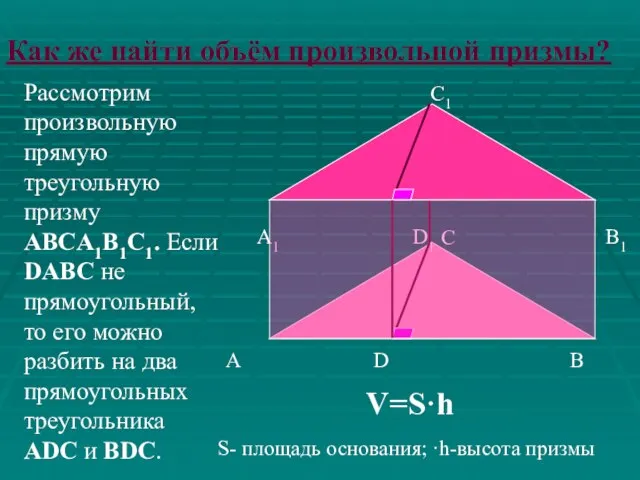
Рассмотрим произвольную прямую треугольную призму ABCA1B1C1. Если DABC не прямоугольный, то его можно разбить на два прямоугольных треугольника ADC и BDC.
A D B
A1 D1 B1
C1
C
Как же найти объём произвольной призмы?
V=S·h
S- площадь основания; ·h-высота призмы

По свойству объемов, сложив объемы этих треугольных призм, получим объем данной.
Ф1
Ф2
Ф3
V=V1 +V2 +V3
Пусть дана n – угольная прямая призма (n>3).
Разобьем ее на конечное число прямых треугольных призм.
V=S1·h+S2·h+S3·h
V=S·h