Слайд 2Цель: Исследование роли «геометрического построения на плоскости» в геометрии и архитектуре.
Задачи:
1.Изучить

научную литературу, ресурсы сети Интернет по исследуемой теме.
2.Выявить роль задач на построение сечений в геометрии, архитектуре.
3.Показать:
а) непосредственную связь геометрии и архитектуры.
б) прикладные возможности задач на построение сечений.
в) значимость задач в развитии современной науки.
Слайд 3ПЛАН
1. Введение.
2. Из истории начертательной геометрии.
3. Виды проецирования.
1) центральное проецирование;
2)

параллельное проецирование;
3) основные независимые свойства параллельного проецирования.
4. Пересечение многогранников плоскостью.
1) методы построения сечений многогранников:
- метод следов;
- решение задач на построение сечений многогранников;
- способ внутреннего проектирования;
- решение задач на построение сечений многогранников.
5. Конические сечения.
1) ранняя история;
2) построение конических сечений:
- эллипс;
- гипербола;
- парабола.
3) свойства конических сечений:
- определения Папа;
- конструкция Данделена;
- другие свойства.
4) аналитический подход:
- алгебраическая классификация;
- вывод уравнений конических сечений.
5) проективный подход;
6) специальные построения;
6. Заключение.
7. Список используемой литературы
Слайд 5 Из истории начертательной геометрии
Гаспар Монж
Сергей Курдюмов

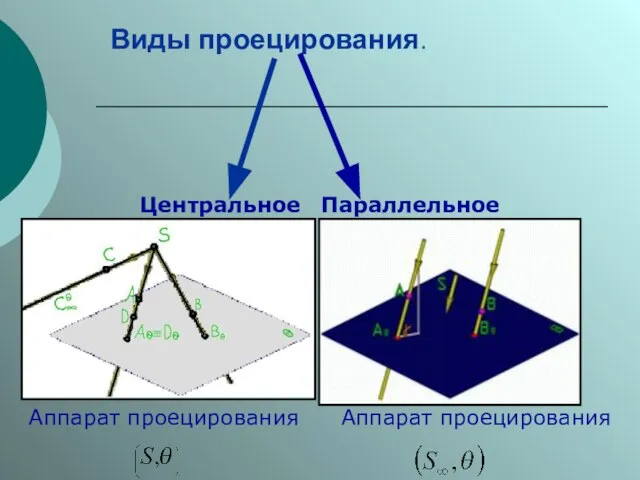
Слайд 6 Виды проецирования.
Центральное
Параллельное
Аппарат проецирования
Аппарат проецирования
Слайд 7 Пересечение
многогранников плоскостью.
Центральное проецирование используется -
при построении сечений пирамиды,

вершина пирамиды центр проецирования
Слайд 8Пересечение
многогранников плоскостью.
Параллельное проецирование
используется
при построении сечений призм.

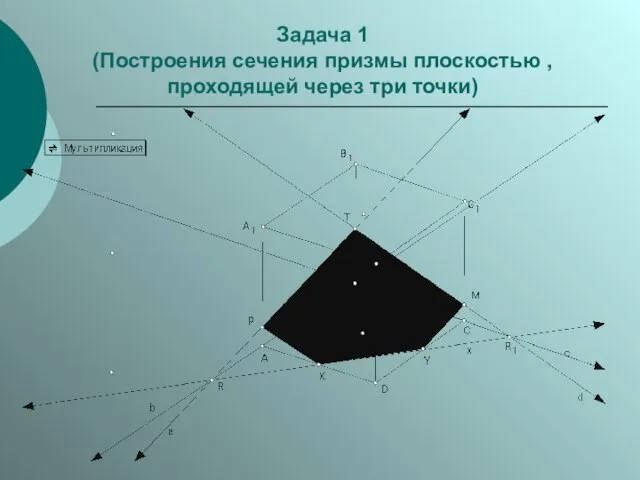
Слайд 9Задача 1
(Построения сечения призмы плоскостью , проходящей через три точки)
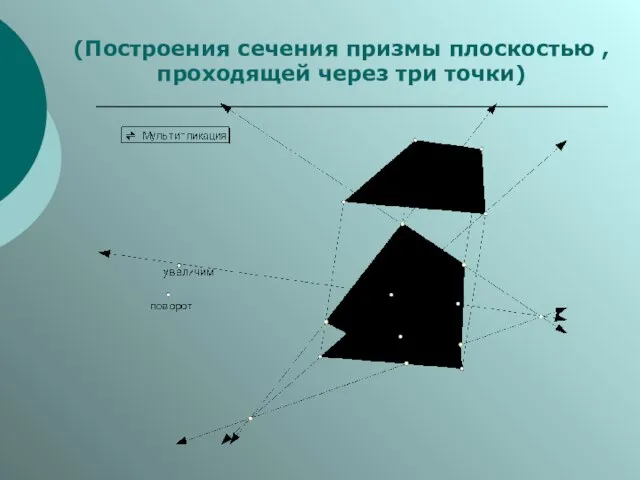
Слайд 10
(Построения сечения призмы плоскостью ,
проходящей через три точки)
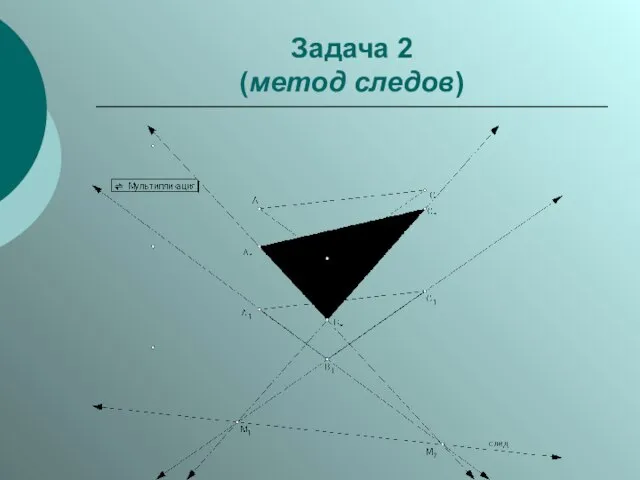
Слайд 12Задача 3
(способ внутреннего проектирования)

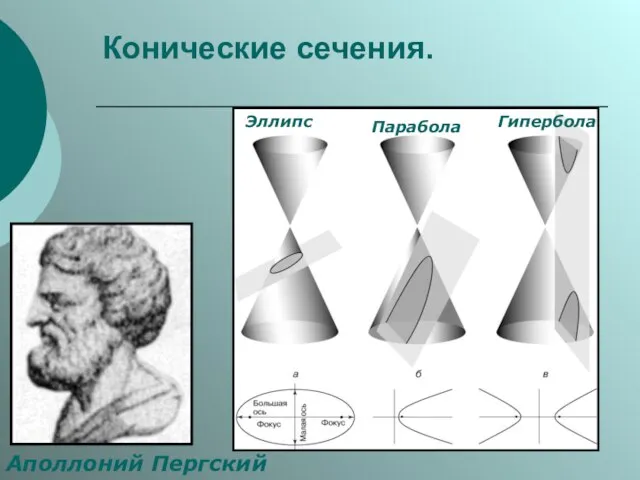
Слайд 13Конические сечения.
Аполлоний Пергский
Эллипс
Парабола
Гипербола
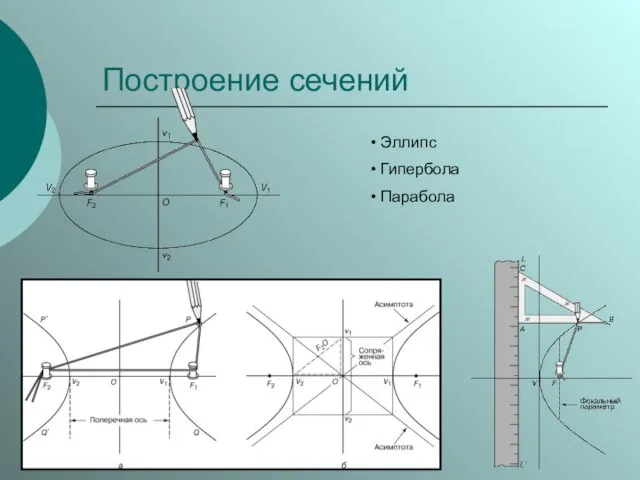
Слайд 14Построение сечений
Эллипс
Гипербола
Парабола
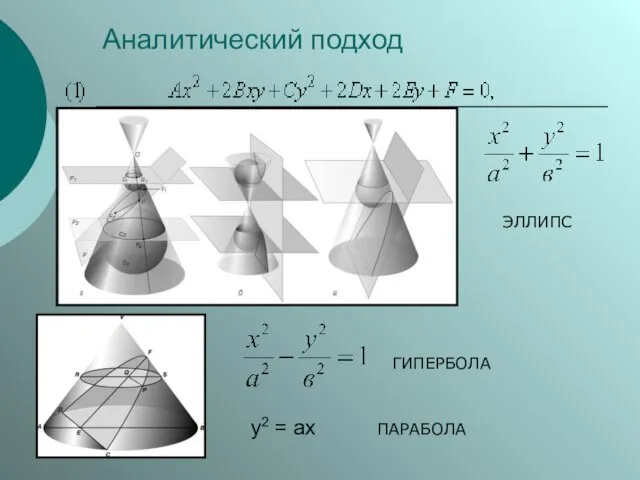
Слайд 15Аналитический подход
y2 = ax
ЭЛЛИПС
ГИПЕРБОЛА
ПАРАБОЛА
Слайд 17 Заключение.
Геометрия в архитектуре.
Геометрия в архитектуре
ЗАКЛЮЧЕНИЕ

Слайд 26Искусство не есть одна наука,
искусство пользуется наукой ,
искусство должно уметь

законы и знания применять к делу
(П.П.Чистяков.)
























 В гостях у Геометрии - презентация по Геометрии_
В гостях у Геометрии - презентация по Геометрии_ Геометрия 7 класс Геометрия 7 класс
Геометрия 7 класс Геометрия 7 класс УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА"
УСТНЫЕ ЗАДАЧИ ПО ТЕМЕ "ПРИЗМА" Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья
Метод площадей при решении геометрических задач Выполнил: ученик 10 Б класса МОУ «Лицей №15» им. акад. Ю.Б. Харитона Сулоев Илья 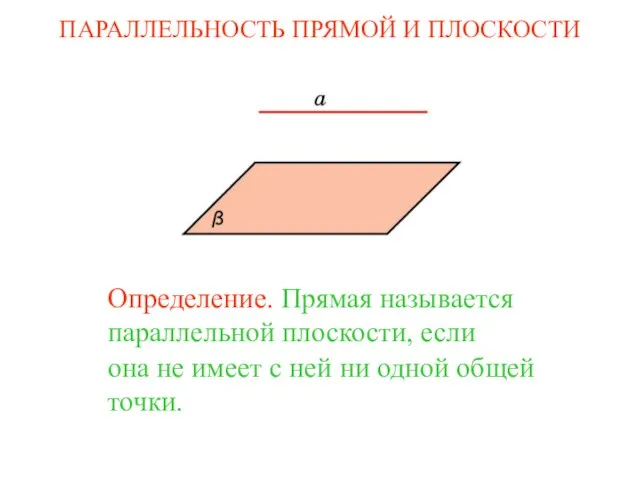 Параллельность прямой и плоскости
Параллельность прямой и плоскости Магические квадраты (5 класс)
Магические квадраты (5 класс) Определение параллельных прямых
Определение параллельных прямых Трехгранный угол
Трехгранный угол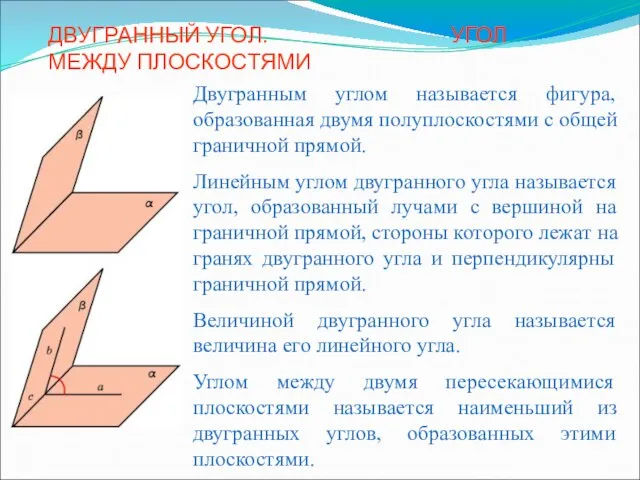 Двугранный угол. Угол между плоскостями4
Двугранный угол. Угол между плоскостями4 Прямоугольный параллелепипед
Прямоугольный параллелепипед Правильные выпуклые многогранники
Правильные выпуклые многогранники Геометрические задачи «С2» - презентация по Геометрии_
Геометрические задачи «С2» - презентация по Геометрии_ Параллельные прямые 6 класс
Параллельные прямые 6 класс Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми
Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми Равнобедренный треугольник
Равнобедренный треугольник Пифагоровы штаны во все стороны равны
Пифагоровы штаны во все стороны равны Нахождение угла между скрещивающимися прямыми
Нахождение угла между скрещивающимися прямыми Объем наклонной призмы, пирамиды и конуса
Объем наклонной призмы, пирамиды и конуса Пирамиды
Пирамиды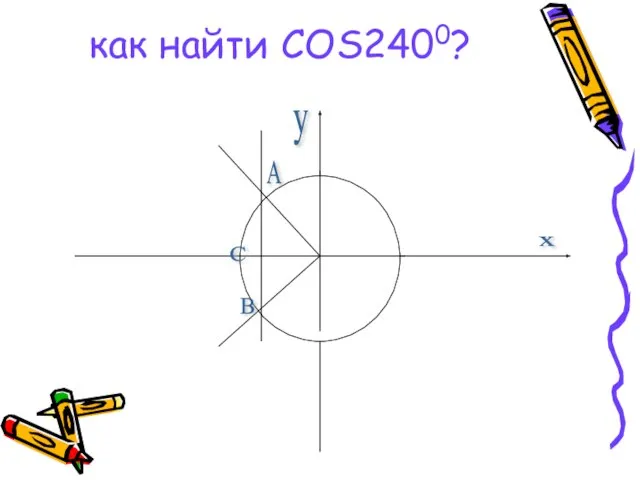 Косинус
Косинус Векторы: Знакомство
Векторы: Знакомство Площадь параллелограмма и треугольника
Площадь параллелограмма и треугольника Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА
Элементы тригонометрии РАДИАННАЯ МЕРА УГЛА Геометрия 8класс Учитель Бужан Л.В.
Геометрия 8класс Учитель Бужан Л.В. Вычисление площадей фигур в ходе экспериментальной деятельности
Вычисление площадей фигур в ходе экспериментальной деятельности Площадь прямоугольника
Площадь прямоугольника Развитие геометрии
Развитие геометрии Перпендикулярность в пространстве (10 класс)
Перпендикулярность в пространстве (10 класс)