Содержание
- 2. Иерархия классов методов моделирования Характерные масштабы размеров систем Атомистическое моделирование. Главной особенностью данного класса методов является
- 3. Иерархия классов методов моделирования Характерные масштабы размеров систем Микроскопическое моделирование. Для этого типа моделирования детализация описания
- 4. Иерархия классов методов моделирования Характерные масштабы размеров систем Мезоскопическое моделирование. основную роль играют микроструктурные элементы, такие
- 5. Иерархия классов методов моделирования Характерные масштабы размеров систем Макроскопическое моделирование. система рассматривается как сплошная среда (континуум),
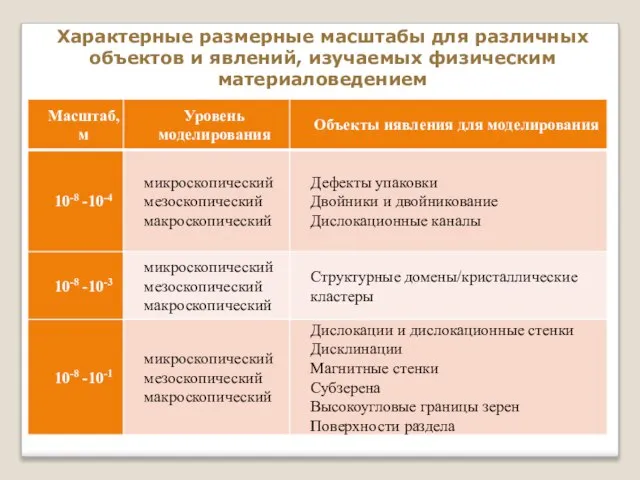
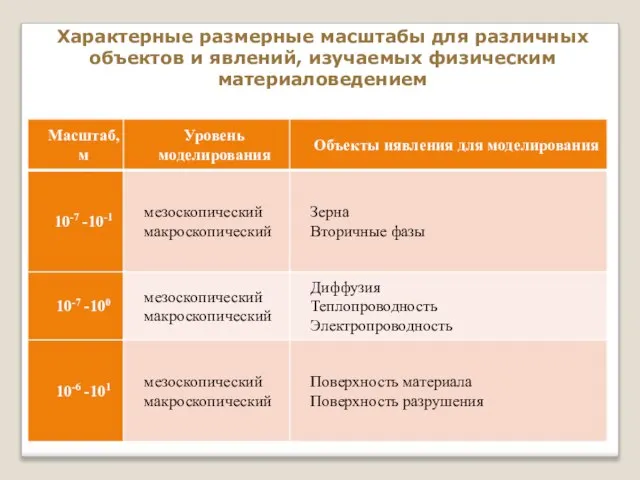
- 6. Характерные размерные масштабы для различных объектов и явлений, изучаемых физическим материаловедением
- 7. Характерные размерные масштабы для различных объектов и явлений, изучаемых физическим материаловедением
- 8. Характерные размерные масштабы для различных объектов и явлений, изучаемых физическим материаловедением
- 9. Атомистические и микроскопические методы Наиболее практически важными величинами, определяемыми в численных экспериментах на атомарном уровне, являются
- 10. Атомистические и микроскопические методы ЗАЧЕМ ??? полная энергия
- 11. Атомистические и микроскопические методы ЗАЧЕМ ??? нам нужна полная энергия , для чего она используется ?
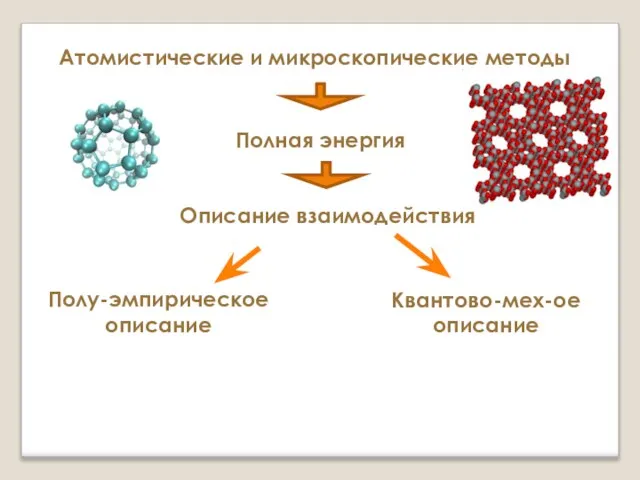
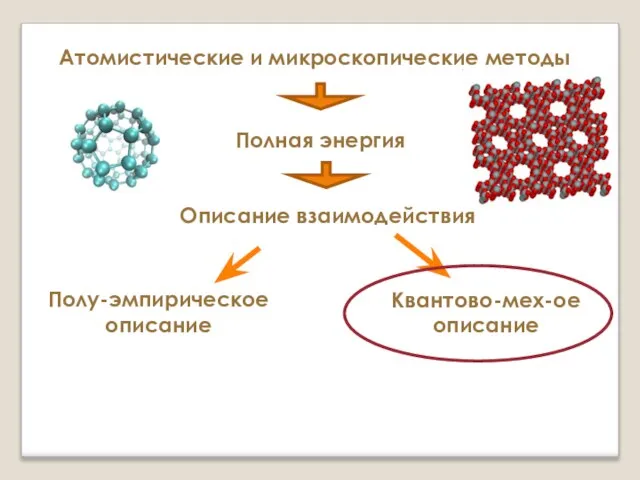
- 12. Атомистические и микроскопические методы Полная энергия Полу-эмпирическое описание Квантово-мех-ое описание Описание взаимодействия
- 13. Атомистические и микроскопические методы Полная энергия Полу-эмпирическое описание Квантово-мех-ое описание Описание взаимодействия
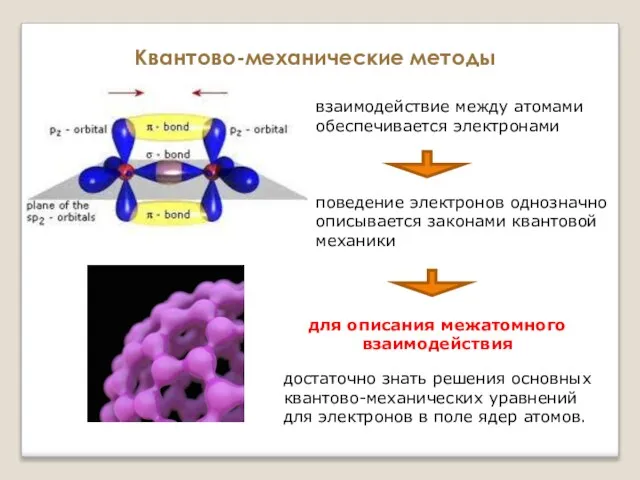
- 14. Квантово-механические методы взаимодействие между атомами обеспечивается электронами поведение электронов однозначно описывается законами квантовой механики для описания
- 15. Квантово-механические методы квантово-механические уравнения : уравнение Шредингера Нобелевская премия по физике, Медаль имени Макса Планка Нерелятивистское
- 16. Квантово-механические методы квантово-механические уравнения : уравнение Шредингера Нобелевская премия по физике, Медаль имени Макса Планка 1926
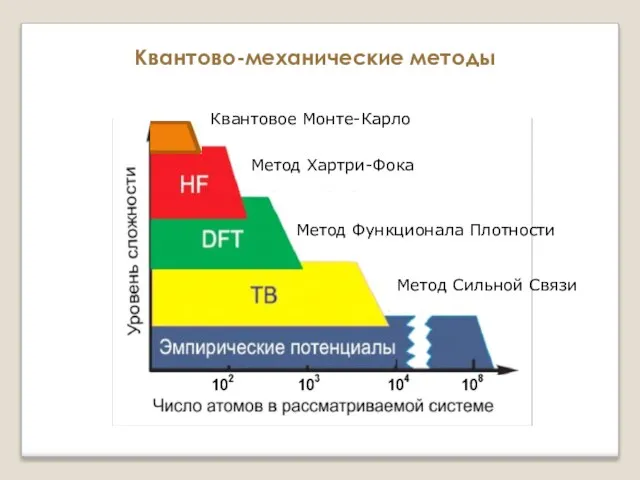
- 17. Квантово-механические методы Метод Хартри-Фока Метод Функционала Плотности Метод Сильной Связи Квантовое Монте-Карло
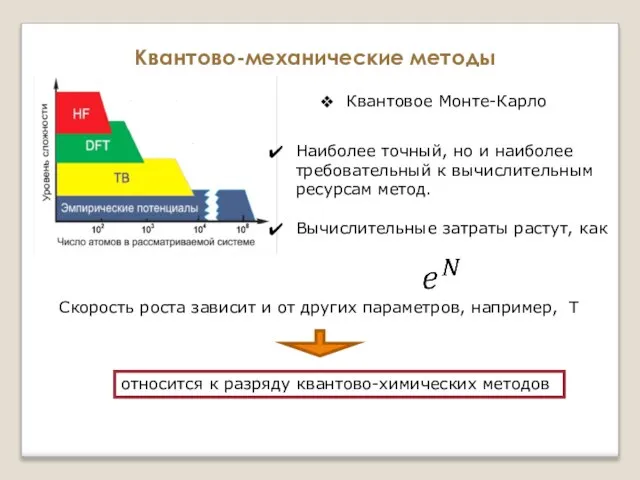
- 18. Квантово-механические методы Квантовое Монте-Карло Наиболее точный, но и наиболее требовательный к вычислительным ресурсам метод. Вычислительные затраты
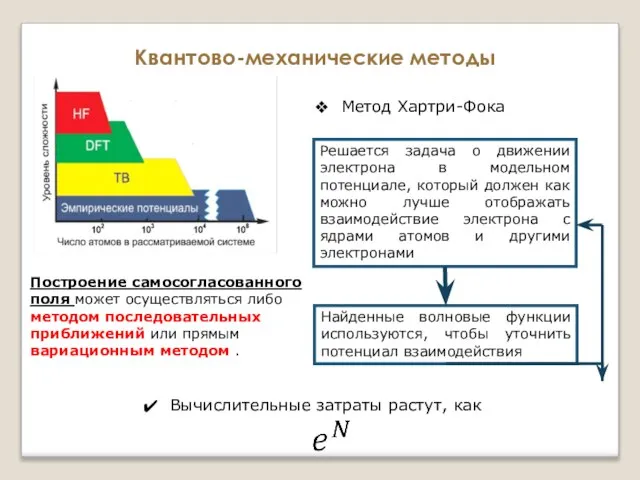
- 19. Квантово-механические методы Метод Хартри-Фока приближённый метод решения уравнения Шрёдингера путём сведения многочастичной задачи к одночастичной в
- 20. Квантово-механические методы Метод Хартри-Фока Решается задача о движении электрона в модельном потенциале, который должен как можно
- 21. Квантово-механические методы Метод Теории Функционала Плотности наиболее распространенный перво-принципный метод, используемый в задачах материаловедения использует более
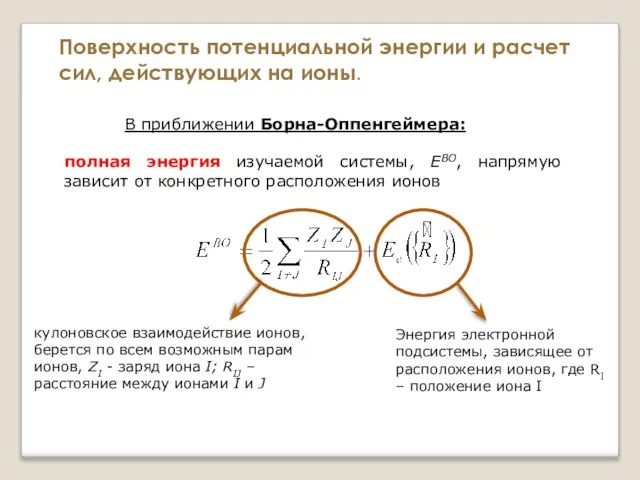
- 22. моментальные положения ионов являются параметрами уравнения Шредингера для электронов энергия электронной подсистемы Ee является функцией координат
- 23. полная энергия изучаемой системы, EBO, напрямую зависит от конкретного расположения ионов Поверхность потенциальной энергии и расчет
- 24. Поверхность потенциальной энергии и расчет сил, действующих на ионы. Можно рассматривать потенциальную энергию Борна-Оппенгеймера как многомерную
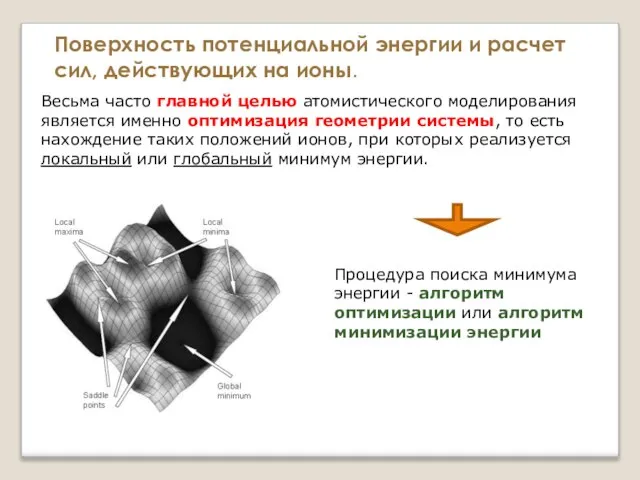
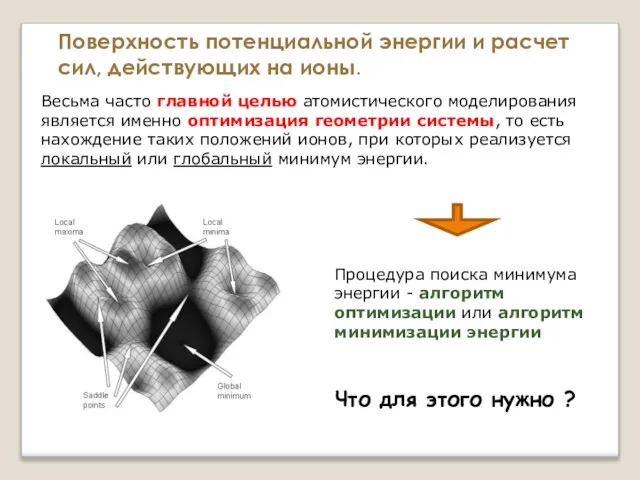
- 25. Весьма часто главной целью атомистического моделирования является именно оптимизация геометрии системы, то есть нахождение таких положений
- 26. Весьма часто главной целью атомистического моделирования является именно оптимизация геометрии системы, то есть нахождение таких положений
- 27. ! При исследовании динамического поведения ионов, а также в ряде наиболее эффективных алгоритмов минимизации энергии необходимо
- 28. Расчет сил, действующих на ионы Когда энергия задана как аналитическая функция ионных координат, ее вычисление не
- 29. Даже имея возможность рассчитывать только полные энергии, можно численно оценить силы на отдельные ионы, если придавать
- 30. Расчет сил, действующих на ионы теорема Хеллмана-Фейнмана Для вычисления такого среднего достаточно знания тех же одноэлектронных
- 31. Расчет сил, действующих на ионы теорема Хеллмана-Фейнмана силы вычисленные с помощью теоремы Хеллмана-Фейнмана очень чувствительны к
- 32. Атомистические и микроскопические методы Молекулярная статика Молекулярная динамика Главной задачей является нахождение состояния системы с минимальной
- 33. Методы молекулярной статики
- 34. Главной задачей является нахождение состояния системы с минимальной энергией (или основного состояния). Используется при исследовании :
- 35. Суть метода - математические методы минимизации для случая, когда минимизируемой функцией является полная потенциальная энергия системы.
- 36. Молекулярная статика Математическая задача минимизация функции многих переменных: Задана функция U, которая однозначно зависит от некоторого
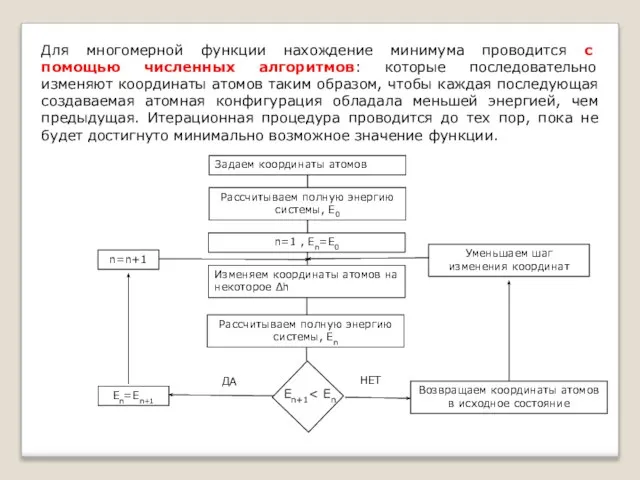
- 37. Для многомерной функции нахождение минимума проводится с помощью численных алгоритмов: которые последовательно изменяют координаты атомов таким
- 38. Молекулярная статика Алгоритмы минимизации энергии системы принято разделять на: те, которые используют производные энергии по координатам
- 39. Молекулярная статика: Методы Поиска Методы Поиска используют только значения самой функции. МИНУСЫ МЕТОДА Методы поиска, как
- 40. Молекулярная статика: Градиентные методы. В семействе Градиентных методов предполагается, что для любой точки фазового пространства возможно
- 41. Молекулярная статика: Градиентные методы. Существует целый набор методов, относящихся к семейству Градиентных методов: метод наискорейшего спуска
- 42. Молекулярная статика: Методы Ньютона . Методы Ньютона используют первые и вторые производные энергии. ПЛЮСЫ МЕТОДА Это
- 43. Молекулярная статика: Методы Ньютона . Использование производных при нахождении минимумов функций - чрезвычайно полезно, поскольку они
- 44. Молекулярная статика: Методы Ньютона . Знание направления и величины градиента энергии в любой точке позволяет выбрать
- 45. Молекулярная статика: Методы Ньютона . Вторые производные потенциальной энергии дают информацию о локальной кривизне энергетической поверхностности.
- 46. максимум - все собственные значения отрицательны, минимум - все собственные значения положительны седловая точка - некоторые
- 47. Методы первого порядка не в состоянии строго следовать дну энергетической долины, если не применяются дополнительные процедуры
- 49. Скачать презентацию


































 Презентация на тему Полимеразная цепная реакция
Презентация на тему Полимеразная цепная реакция  Понятие о химической реакции. Реакции, идущие без изменения состава веществ. 11 класс
Понятие о химической реакции. Реакции, идущие без изменения состава веществ. 11 класс Презентация на тему Химическая связь (8 класс)
Презентация на тему Химическая связь (8 класс)  Классы неорганических веществ
Классы неорганических веществ Металлы. 9 класс
Металлы. 9 класс Примеры реакций в жизни и в быту. Реакции по направлению процесса
Примеры реакций в жизни и в быту. Реакции по направлению процесса Виды химической связи
Виды химической связи Общие способы получения металлов
Общие способы получения металлов Практическая работа №5. Качественные реакции на анионы 1-3 групп
Практическая работа №5. Качественные реакции на анионы 1-3 групп Классификация реакций
Классификация реакций Электролитическая диссоциация
Электролитическая диссоциация Структура неорганических ионных соединений. Лекция 12
Структура неорганических ионных соединений. Лекция 12 Материаловедение. Стали. Свойства сталей. Классификация сталей
Материаловедение. Стали. Свойства сталей. Классификация сталей Основы химической термодинамики
Основы химической термодинамики Сравнительная характеристика стиральных порошков
Сравнительная характеристика стиральных порошков Алкадиены
Алкадиены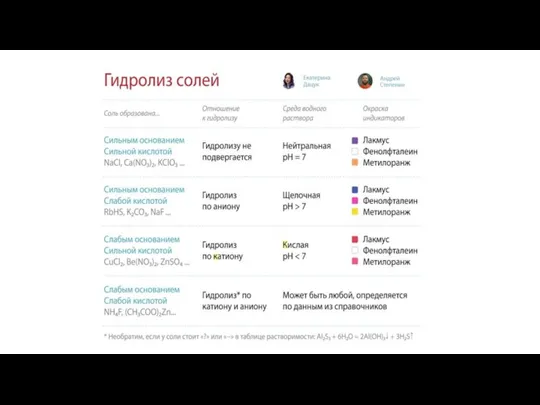 Гидролиз солей
Гидролиз солей Химическое равновесие. Экзаменационные вопросы
Химическое равновесие. Экзаменационные вопросы Генетическая связь неорганических соединений
Генетическая связь неорганических соединений Презентация на тему Круговорот углерода в природе
Презентация на тему Круговорот углерода в природе  Рука руку моет. Механизм двух реакций
Рука руку моет. Механизм двух реакций Презентация на тему Пестициды
Презентация на тему Пестициды  Свойства радиоактивных элементов
Свойства радиоактивных элементов Металлы и неметаллы. Знакомство с периодической системой Д. И. Менделеева
Металлы и неметаллы. Знакомство с периодической системой Д. И. Менделеева Оценка качества пищевой соли, реализуемой в розничной торговле
Оценка качества пищевой соли, реализуемой в розничной торговле Соли Na2SO4
Соли Na2SO4 Окислительно-восстановительные реакции. Электролиз
Окислительно-восстановительные реакции. Электролиз Углеводороды. Характеристика
Углеводороды. Характеристика