Содержание
- 2. При изучении любых химических систем используют термодинамический и кинетический подход. В термодинамическом подходе рассматривают конечное и
- 3. Термодинамическая система – тело или группа тел, которые нас интересуют, все остальное – окружающая среда. По
- 4. Первое Начало утверждает, что теплота, переданная системе, идет на увеличение ее внутренней энергии и на работу
- 5. ИЗМЕНЕНИЕ ЭНТАЛЬПИИ СИСТЕМЫ В ХОДЕ ХИМИЧЕСКИХ РЕАКЦИЙ
- 6. Закон Кирхгофа гласит, что температурный коэффициент теплового эффекта химической реакции равен изменению теплоемкости системы в ходе
- 7. Поскольку многие химические процессы являются обратимыми, т.е. протекают в прямом и обратном направлении, необходимо помнить, что
- 8. НАПРАВЛЕННОСТЬ САМОПРОИЗВОЛЬНОГО ПРОТЕКАНИЯ ПРОЦЕССА Стремление системы к минимуму энергии – не единственная причина возможности самопроизвольного протекания
- 9. S = k ln W S – энтропия (функция состояния), от греч.trope – обращение, изменение. Размерность
- 10. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ЭНЕРГИЯ ГИББСА . В ИЗОЛИРОВАННОЙ СИСТЕМЕ ВОЗМОЖНЫ ТОЛЬКО ТАКИЕ ПРОЦЕССЫ, КОТОРЫЕ СОПРОВОЖДАЮТСЯ РОСТОМ
- 11. ЭНЕРГИЯ ГИББСА
- 13. Скачать презентацию
Слайд 2При изучении любых химических систем используют термодинамический и кинетический подход. В термодинамическом
При изучении любых химических систем используют термодинамический и кинетический подход. В термодинамическом

Расчет изменения значений некоторых функций в заданных условиях позволяет сделать вывод о теоретической возможности самопроизвольного протекания какого-либо процесса в данной системе или указать условия, при которых этот процесс возможен.
В кинетическом подходе главное внимание уделяется описанию пути процесса из исходного в конечное состояние (например, стадии реакции, промежуточные вещества, скорость процесса или отдельных его стадий и т.д.).
Исторически термодинамика, как раздел физики, возникла при изучении теплоты, работы и температуры. В термодинамике стали использовать определенные приемы для описания различных процессов, которые используются и для описания химических реакций, так появилась химическая термодинамика.
Таким образом, химическая термодинамика изучает условия устойчивости химических систем и закономерности их перехода из одного состояния в другое и оперирует следующими основными понятиями:
Слайд 3Термодинамическая система – тело или группа тел, которые нас интересуют, все остальное
Термодинамическая система – тело или группа тел, которые нас интересуют, все остальное

изолированные системы – которые не обмениваются ни веществом (массой), ни энергией с окружающей средой;
закрытые (замкнутые) системы - с окружающей средой веществом не обмениваются, но могут обмениваться энергией (обычно, в виде теплоты);
открытые системы – системы, которые обмениваются с окружающей средой и энергией, и веществом. Это реальные, наиболее часто встречающиеся и наиболее сложные системы. Очень часто, теоретически описывая процессы, считают, что они протекают в изолированных или закрытых системах, как в наиболее простых.
Для описания состояния системы пользуются параметрами состояния: T - температура, P - давление, V – объем, n – количество моль, иногда концентрации Ci. Параметры состояния взаимосвязаны, их взаимосвязь – уравнение состояния.
Например, уравнение состояния идеального газа: pV = nRT.
Слайд 4Первое Начало утверждает, что теплота, переданная системе, идет на увеличение ее внутренней
Первое Начало утверждает, что теплота, переданная системе, идет на увеличение ее внутренней

ΔQ = ΔU + ΔA = ΔU + pΔV ( ΔA = pΔV )
ΔU имеет размерность [Дж]
V = const → QV = ΔU => в случае изохорного процесса теплота, переданная системе идет на увеличение ее внутренней энергии
p = const → ΔQp = ΔU + pΔV = Δ(U + pV)
U + pV ≡ H → U = H – pV
ΔH – энтальпия (теплосодержание, от греч. enthalpein - нагревать), размерность [кДж/моль], функция состояния, функция экстенсивная – зависит от количества вещества.
ΔQp = ΔU + pΔV = ΔH => при изобарном процессе теплота, переданная системе, идет на увеличение ее энтальпии.
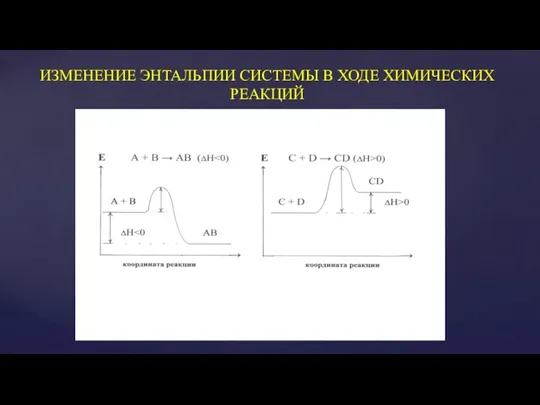
ΔH ˃0 эндотермический процесс, тепло поглощается;
ΔH˂0 экзотермический процесс, тепло выделяется.
ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИ
Слайд 5ИЗМЕНЕНИЕ ЭНТАЛЬПИИ СИСТЕМЫ В ХОДЕ ХИМИЧЕСКИХ РЕАКЦИЙ
ИЗМЕНЕНИЕ ЭНТАЛЬПИИ СИСТЕМЫ В ХОДЕ ХИМИЧЕСКИХ РЕАКЦИЙ
Слайд 6Закон Кирхгофа гласит, что температурный коэффициент теплового эффекта химической реакции равен изменению
Закон Кирхгофа гласит, что температурный коэффициент теплового эффекта химической реакции равен изменению

aA + bB+ … → dD + eE+…
ΔH2 = ΔH1+ ΔCp(T2 – T1),
где ΔH2 и ΔH1 - энтальпии процессов при T1 и T2 соответственно (ΔT невелико).
ΔCp = [dCp(D) + e dCp(E)+….] – [aCp(A)+ bCp(B)+…],
ΔCp(X) – молярная теплоемкость веществ, участвующих в реакции при постоянном давлении (p=const), размерность ΔCp(X) - [Дж/моль•К].
QV = ΔU = nCVΔT, где CV - молярная теплоемкость веществ, участвующих в реакции при постоянном объеме (V =const).
ЗАКОН КИРХГОФА
Слайд 7Поскольку многие химические процессы являются обратимыми, т.е. протекают в прямом и обратном
Поскольку многие химические процессы являются обратимыми, т.е. протекают в прямом и обратном

∆Нпр = - ∆ Нобр,
где ∆Нпр и ∆Нобр – тепловые эффекты (энтальпии) прямой и обратной реакции.
Почему наблюдаются тепловые эффекты при протекании реакций?
Существование тепловых эффектов реакций обусловлено неравенством внутренних энергий реагентов (Up) и продуктов реакций (Uпр), как следует из определения энтальпии: ∆Н=(Uпр-Up)+ p(Vпр-Vp). Чем больше различие (Uпр-Up), тем значительнее величина теплового эффекта ∆Н, работа расширения может отсутствовать. Неравенство внутренних энергий реагентов и продуктов реакции обусловлено различием энергий их химических связей, именно это различие является главной причиной теплового эффекта. Этот вывод подтверждается расчетами величин ΔН с использованием значений энергий связей продуктов и реагентов.
ЭНТАЛЬПИЯ
Слайд 8 НАПРАВЛЕННОСТЬ САМОПРОИЗВОЛЬНОГО ПРОТЕКАНИЯ ПРОЦЕССА
Стремление системы к минимуму энергии – не единственная
НАПРАВЛЕННОСТЬ САМОПРОИЗВОЛЬНОГО ПРОТЕКАНИЯ ПРОЦЕССА Стремление системы к минимуму энергии – не единственная

Слайд 9S = k ln W
S – энтропия (функция состояния), от греч.trope
S = k ln W
S – энтропия (функция состояния), от греч.trope

С ростом температуры энтропия всегда возрастает. Возрастает она и при переходе твердое состояние → жидкое → газообразное. В ходе химических реакций энтропия может как возрастать, так и убывать. Δ S функция экстенсивная, зависит от количества вещества.
CaCO3 (тв) →CaO(тв) + CO2(газ) ΔS˃0; N2(газ) + 3 H2(газ) → 2NH3 (газ) Δ S˂0
М.Планк (1911 г.) «Энтропия идеального кристалла при абсолютном нуле равна нулю».
ЭНТРОПИЯ
Слайд 10ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ЭНЕРГИЯ ГИББСА
.
В ИЗОЛИРОВАННОЙ СИСТЕМЕ ВОЗМОЖНЫ ТОЛЬКО ТАКИЕ ПРОЦЕССЫ, КОТОРЫЕ
ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ. ЭНЕРГИЯ ГИББСА
.
В ИЗОЛИРОВАННОЙ СИСТЕМЕ ВОЗМОЖНЫ ТОЛЬКО ТАКИЕ ПРОЦЕССЫ, КОТОРЫЕ

ΔH = ΔG + TΔS (T, p = const ). ΔG = ̶ Амах Если ΔG ˂0 процесс возможен;
если ΔG ˃0 процесс не возможен.
ΔG = ΔH - TΔS (T,p =const).
H2 (газ) + 1/2 O2 (газ) = H2O (ж) ΔH = ̶ 16,3 кДж При низких температурах TΔS мало и
|ΔH |˃˃|TΔS|, а ΔG ≈ ̶ ΔH;
H2 (газ) + 1/2 O2 (газ) → H2O (ж) ;
При высоких температурах Т – велика, следовательно, |ΔH |˂˂|TΔS| и ΔG ≈ ̶ TΔS
H2 (газ) + 1/2 O2 (газ) ← H2O (ж)
Слайд 11
ЭНЕРГИЯ ГИББСА
ЭНЕРГИЯ ГИББСА

 Фосфор в природе
Фосфор в природе Катализ в нефтепереработке
Катализ в нефтепереработке Количество вещества
Количество вещества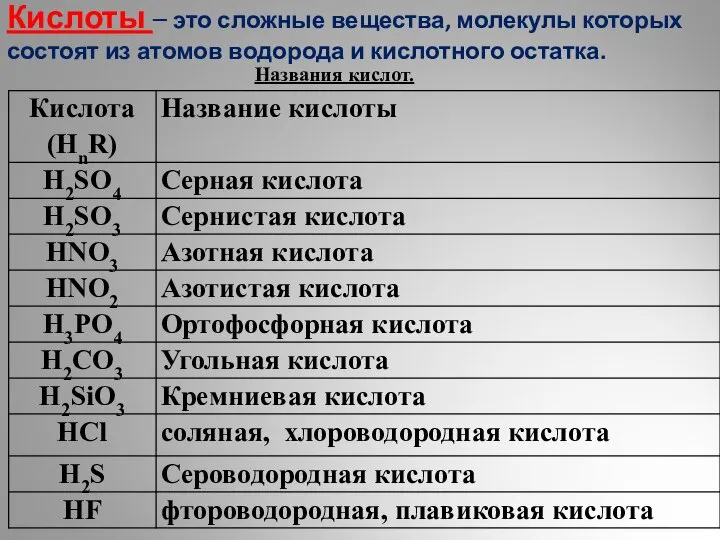 Кислоты. Классификация
Кислоты. Классификация Строение органических веществ
Строение органических веществ Степени окисления
Степени окисления Зонная структура металлов, диэлектриков и полупроводников. Лекция 3
Зонная структура металлов, диэлектриков и полупроводников. Лекция 3 Введение в медицинскую химию: от молекулы к лекарству
Введение в медицинскую химию: от молекулы к лекарству Диаграмма состояния железо-цементит
Диаграмма состояния железо-цементит Номенклатура органических веществ
Номенклатура органических веществ Основы химической кинетики
Основы химической кинетики Пластмассы
Пластмассы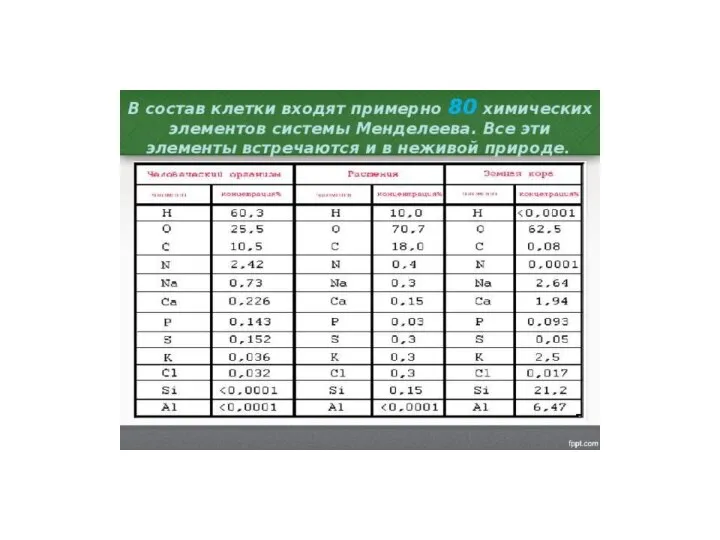 Состав клетки
Состав клетки Металлы
Металлы Экстракция молибдена из азотнокислых растворов карбамоилметилфосфиноксидом, растворенным в высших спиртах
Экстракция молибдена из азотнокислых растворов карбамоилметилфосфиноксидом, растворенным в высших спиртах Презентация на тему Вещества и их свойства
Презентация на тему Вещества и их свойства 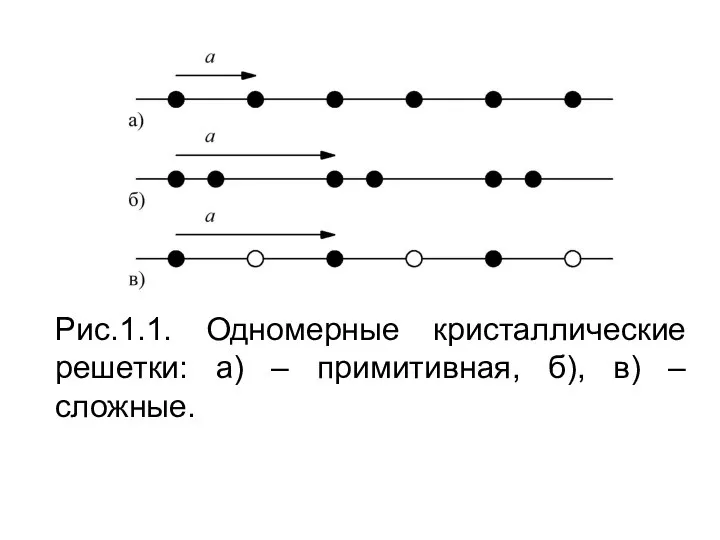 Кристаллические решётки
Кристаллические решётки Вода знакомая и не знакомая
Вода знакомая и не знакомая Взаимодействие элементов-неметаллов между собой. 8 класс
Взаимодействие элементов-неметаллов между собой. 8 класс Основные формулы МКТ
Основные формулы МКТ Гидролиз солей
Гидролиз солей Аметист
Аметист Минерал дунит
Минерал дунит Предельные углеводороды. Алканы, насыщенные углеводороды, парафины, циклоалканы
Предельные углеводороды. Алканы, насыщенные углеводороды, парафины, циклоалканы Истина - дочь времени, а не авторитета
Истина - дочь времени, а не авторитета Формирование и контроль остаточных напряжений, возникающих под действием различных технологических операций
Формирование и контроль остаточных напряжений, возникающих под действием различных технологических операций Химический опыт Черный сахар
Химический опыт Черный сахар ОВР
ОВР