Содержание
- 2. Особенностью молекулярной массы полимеров является ее среднестатистический характер. Усреднение суммы молекулярных масс всех молекул полимера (компонентов
- 3. где Mi – масса i-го компонента (молекулы), Ni – количество i-го компонента (молекулы) Если усреднение ведется
- 4. Как правило, , и отношение называют степенью полидисперсности. Экспериментальные методы определения молекулярной массы полимера Методы определения
- 5. К коллигативным свойствам относят: понижение P насыщенного пара растворителя над раствором (по сравнению с чистым растворителем);
- 6. В зависимости от выбранного коллигативного свойства и, соответственно, метода, определяется либо среднемассовая M , либо среднечисловая
- 8. Таким образом, задача сводится к нахождению мольной концентрации раствора вещества с известной весовой концентрацией. С другой
- 9. Т.о. осмотическое давление зависит от термодинамических свойств растворенного вещества: сегменты полимерных цепей ведут себя как самостоятельные
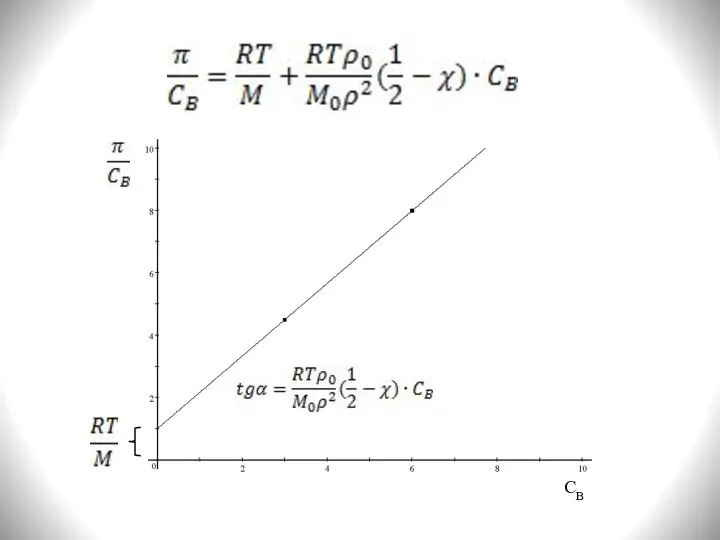
- 10. где ρ0 и M0 – плотность и молекулярная масса растворителя; ρ и M – плотность и
- 11. СB
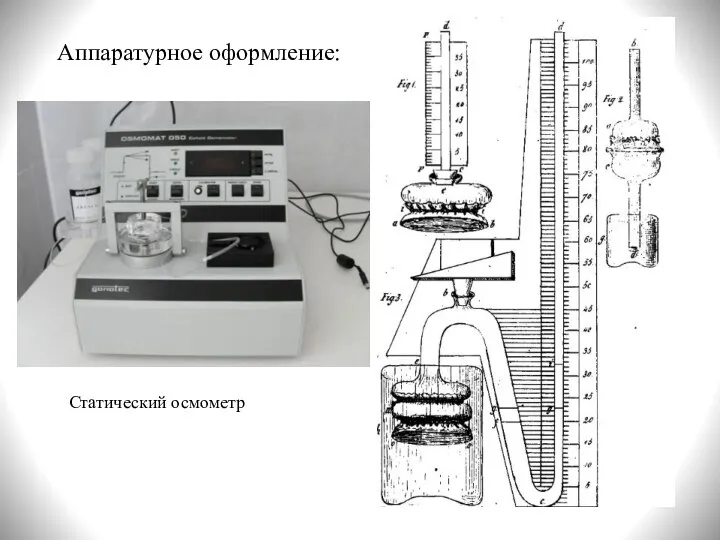
- 12. Аппаратурное оформление: Статический осмометр
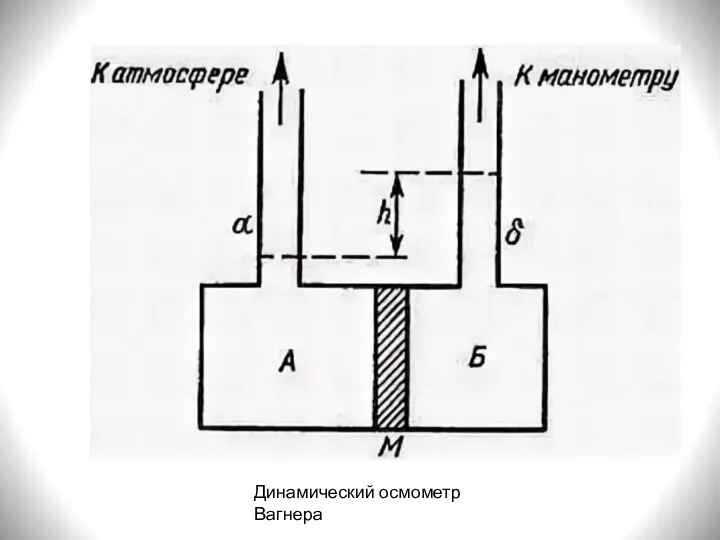
- 13. Динамический осмометр Вагнера
- 14. И в статическом, и в динамическом методах измеряют избыточное давление, которое должно быть приложено к раствору.
- 15. Динамический метод: осмотическое давление определяется путем отслеживания скорости движения мениска в капилляре в зависимости от приложенного
- 16. 2. Вискозиметрический метод Методом вискозиметрии определяется средневязкостная молекулярная масса (отличающаяся от среднемассовой и среднечисловой молекулярной массы).
- 17. Существует следующая взаимосвязь между характеристической, удельной и динамической вязкостью. где [η] – характеристическая вязкость, ηуд –
- 18. А поскольку динамическая вязкость в свою очередь зависит от времени истечения раствора через капилляр вискозиметра по
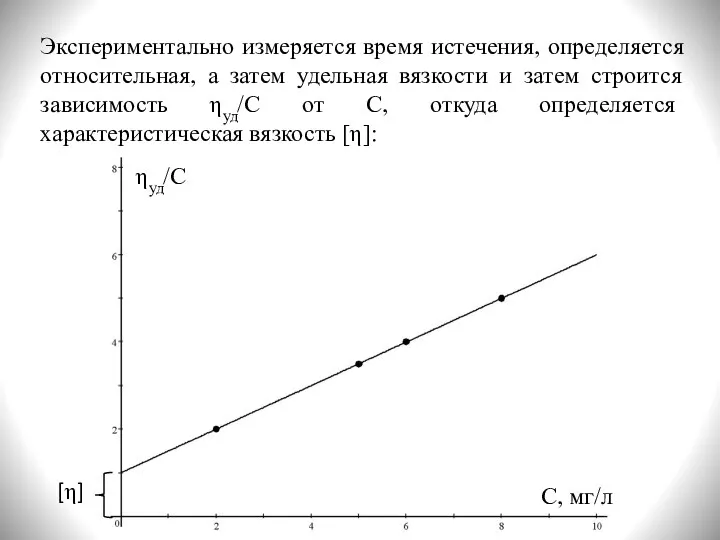
- 19. Экспериментально измеряется время истечения, определяется относительная, а затем удельная вязкости и затем строится зависимость ηуд/С от
- 20. Аппаратурное оформление: вискозиметр Оствальда (определяется время истечения через капилляр) или вискозиметр Убеллоде (определяется давление). Выход на
- 21. Недостатки метода: Тщательность термостатирования (±0,02 С) Зависимость от параметров К и α (которые находятся для полимеров
- 22. Из закона Стокса выводится следующая зависимость молекулярной массы от константы седиментации. где x – расстояние, пройденное
- 23. Коэффициент трения f0 можно выразить через коэффициент диффузии:
- 24. Если далее принять (dx/dt)/(ω2x) за S, называемой константой седиментации (в пределе для растворов с С→0), а
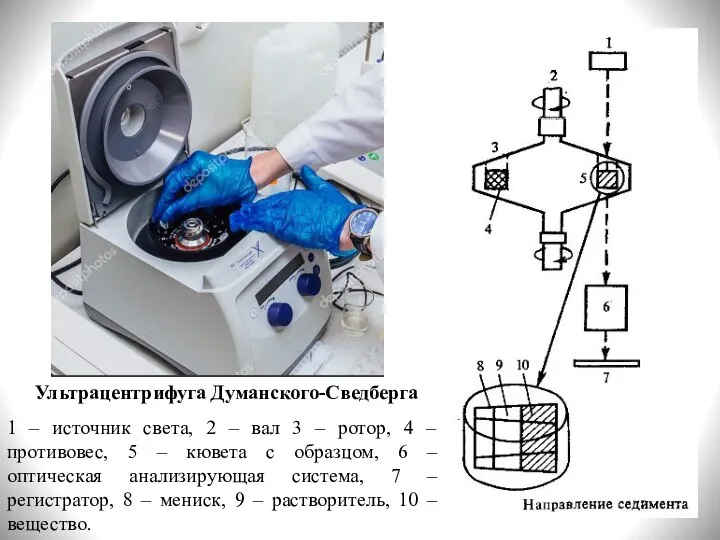
- 25. 1 – источник света, 2 – вал 3 – ротор, 4 – противовес, 5 – кювета
- 27. Скачать презентацию












![Существует следующая взаимосвязь между характеристической, удельной и динамической вязкостью. где [η] –](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1066734/slide-16.jpg)






 Тренажер. Химические свойства солей
Тренажер. Химические свойства солей Презентация по Химии "Законы газового состояния вещества"
Презентация по Химии "Законы газового состояния вещества"  Строение , свойства и биологическая роль гликолипидов. Тема 14
Строение , свойства и биологическая роль гликолипидов. Тема 14 Вещество и тело. Атом и молекула. Свойства веществ. Простые и сложные вещества. Химический элемент
Вещество и тело. Атом и молекула. Свойства веществ. Простые и сложные вещества. Химический элемент Электролитическая диссоциация уксусной и муравьиной кислоты
Электролитическая диссоциация уксусной и муравьиной кислоты Аналитическая химия. Гомогенные растворы
Аналитическая химия. Гомогенные растворы Производство препарата Салициловая кислота, раствор для наружного применения спиртовой 2-х процентный
Производство препарата Салициловая кислота, раствор для наружного применения спиртовой 2-х процентный Углерод и его соединения
Углерод и его соединения Сложные эфиры. Жиры. Мыла
Сложные эфиры. Жиры. Мыла Презентация на тему Подгруппа углерода и азота
Презентация на тему Подгруппа углерода и азота  Реакции обмена
Реакции обмена Углеводы. Классификация углеводов
Углеводы. Классификация углеводов ОВР химияПрезентация
ОВР химияПрезентация Спирты. Классификация
Спирты. Классификация Теория строения химических соединений
Теория строения химических соединений Водород, его общая характеристика, нахождение в природе и его свойства
Водород, его общая характеристика, нахождение в природе и его свойства Карбонильные производные (кислоты, альдегиды, кетоны, сложные эфиры)
Карбонильные производные (кислоты, альдегиды, кетоны, сложные эфиры)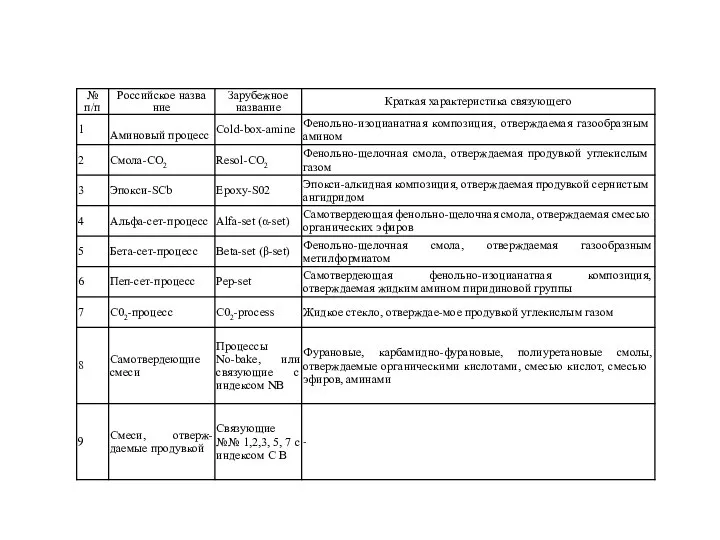 Фенольно-изоцианатная композиция
Фенольно-изоцианатная композиция Взаимное притяжение и отталкивание молекул
Взаимное притяжение и отталкивание молекул Интеллектуальные игры. Химия
Интеллектуальные игры. Химия Презентация на тему Фенол и его свойства
Презентация на тему Фенол и его свойства  Алюминий и его сплавы, их характеристика. Деформируемые сплавы алюминия. Деформируемые и литейные сплавы алюминия
Алюминий и его сплавы, их характеристика. Деформируемые сплавы алюминия. Деформируемые и литейные сплавы алюминия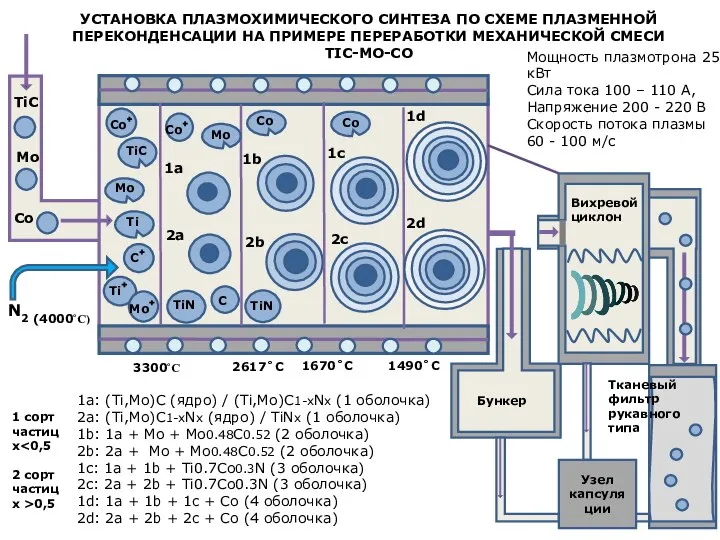 Установка плазмохимического синтеза по схеме плазменной переконденсации на примере переработки механической смеси tic-mo-co
Установка плазмохимического синтеза по схеме плазменной переконденсации на примере переработки механической смеси tic-mo-co Презентация на тему Неметаллы. Мышьяк
Презентация на тему Неметаллы. Мышьяк  Щелочные металлы
Щелочные металлы Пайданалылған майларды қолдана отырып көмірді брикеттер алу
Пайданалылған майларды қолдана отырып көмірді брикеттер алу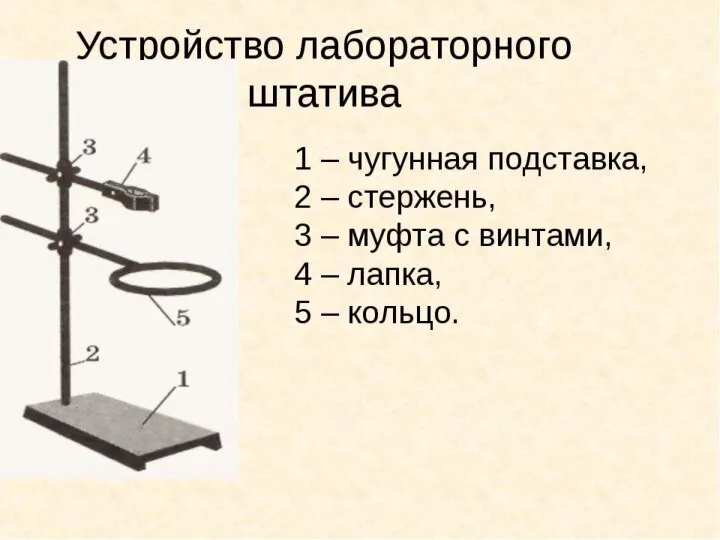 Устройство лабораторного штатива
Устройство лабораторного штатива Жидкая углекислота
Жидкая углекислота