Содержание
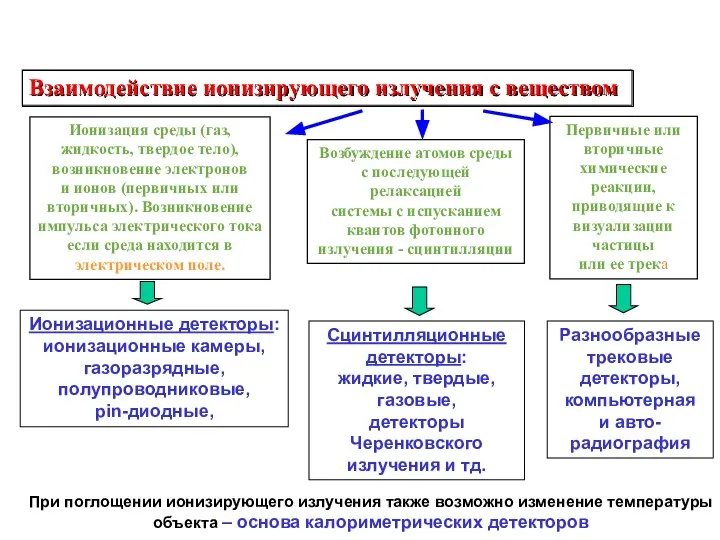
- 2. Взаимодействие ионизирующего излучения с веществом Ионизация среды (газ, жидкость, твердое тело), возникновение электронов и ионов (первичных
- 3. Измерили радиоактивность препарата 58Co35SO4 с помощью торцового счетчика Гейгера-Мюллера с окном толщиной 4 мг/см2. Скорость счета
- 4. Примеры задач для подготовки к контрольной № 1
- 5. Краткая характеристика заданий контрольной работы № 1 Схемы распада, энергия распада, энергия частиц Основной закон радиоактивного
- 6. Задача 6. Зависмость скорости счета от условий измерения Регистрируемая активность I связана с абсолютной активностью А
- 7. Поправка на схему распада p. Доля излучения данного вида (или данной энергии) в спектре испускаемых ядром
- 8. Измерили радиоактивность препарата 58Co35SO4 с помощью торцового счетчика Гейгера-Мюллера с окном толщиной 4 мг/см2. Скорость счета
- 9. Расчетные формулы Поправка на схему распада p - из таблиц изотопов Истинная скорость счета (поправка на
- 10. Решение. Поправка на разрешающее время [Ic = (6100)/60 = 101.67 (имп/с)] I = [Ic/(1-Ic*τ)] – Iфон
- 11. Задачи для домашней подготовки к КР Для измерения активности нуклида *A, содержащегося в препарате толщиной 20
- 12. «Равновесия» Задача (решение на слайде 13) Имеется цепочка превращений 95Zr→95Nb→95Moстаб.. В начальный момент радиоактивность препарата 95Zr,
- 13. Задача «равновесие» Имеется цепочка превращений 95Zr→95Nb→95Moстаб.. В начальный момент радиоактивность препарата 95Zr, очищенного от 95Nb, равнялась
- 14. Задача для домашней подготовки Ниже приведена цепочка превращений: *A→*B→C(стаб.). Нуклид A после очистки от продуктов распада
- 15. III.3. Препарат 210Pb, активность которого после отделения продуктов распада составляла 20 кБк, хранился в лаборатории в
- 16. Решение III.3. Вековое равновесие (по условию t >> 138 сут.) В настоящее время (t) a(210Pb) =
- 17. Задачи «основной закон распада» Удельная радиоактивность океанической воды по 40K составляет 12 кБк/м3. Рассчитайте концентрацию солей
- 18. Основной закон распада. Задачи для домашней подготовки к КР 1. Элемент калий помимо двух стабильных нуклидов
- 20. Скачать презентацию







![Решение. Поправка на разрешающее время [Ic = (6100)/60 = 101.67 (имп/с)] I](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/943842/slide-9.jpg)








 Кислородсодержащие соединения азота
Кислородсодержащие соединения азота Сложные эфиры
Сложные эфиры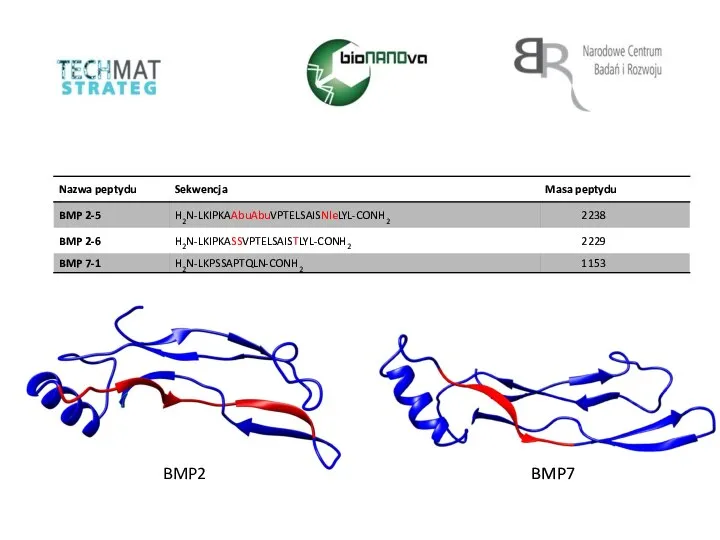 Nazwa peptydu. Sekwencja
Nazwa peptydu. Sekwencja Horenie
Horenie Практическая работа 1. ХТП. Классификация химических реакций
Практическая работа 1. ХТП. Классификация химических реакций Ацетиленовые углеводороды. Алкины
Ацетиленовые углеводороды. Алкины Знаки химических элементов. 8 класс
Знаки химических элементов. 8 класс Строение атома. Строение электронных оболочек атомов
Строение атома. Строение электронных оболочек атомов Хим-1 презент
Хим-1 презент Коррозия металлов
Коррозия металлов Геометрия молекул
Геометрия молекул Взаимодействие кислот с металлами. Кислоты-окислители
Взаимодействие кислот с металлами. Кислоты-окислители Алканы – строение, химические свойства
Алканы – строение, химические свойства Кабинет химии
Кабинет химии Основания. Определение. Формулы
Основания. Определение. Формулы Соли, их классификация и свойства
Соли, их классификация и свойства Презентация на тему Алкины
Презентация на тему Алкины  Сложные эфиры. Жиры
Сложные эфиры. Жиры Химия окислительновосстановительные реакции
Химия окислительновосстановительные реакции Химическая связь
Химическая связь Материалы в промышленности
Материалы в промышленности Графен. Нобелевская премия 2016
Графен. Нобелевская премия 2016 Химия в быту
Химия в быту Анализ катионов и анионов. Лекция № 2
Анализ катионов и анионов. Лекция № 2 Комплексные соединения
Комплексные соединения Типы химической связи
Типы химической связи Атомы химических элементов
Атомы химических элементов Получение и химические свойства металлов
Получение и химические свойства металлов