Содержание
- 2. термодинамическое определение энтропии Энтропия (S) – функция состояния, изменение которой равно теплоте, подведенной к системе в
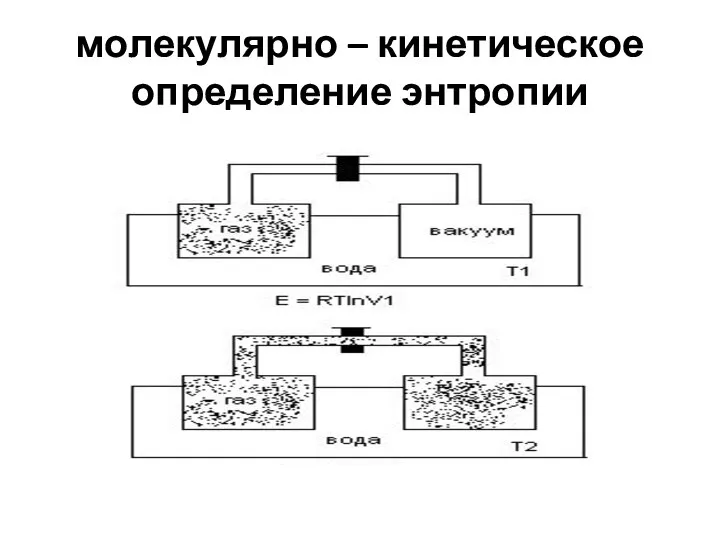
- 3. молекулярно – кинетическое определение энтропии
- 4. Статистическое определение (вероятностный подход) Энтропия – функция состояния, характеризующая степень неупорядоченности системы. Энтропия – логарифмическое выражение
- 5. Второе начало термодинамики Невозможно осуществить перенос тепла от менее нагретого тела к более нагретому (Р.Клаузиус). Каждый
- 6. Расчет изменения энтропии реакции где j − продукты реакции; i − исходные вещества; ν − стехиометрические
- 7. Энтропия зависит от : 1) природы вещества (∆S(СО2)=214 Дж/моль К; (∆S(СО)=198 Дж/моль К) 2) агрегатного состояния
- 8. Третье начало термодинамики (постулат Планка): энтропия идеального ионного кристалла при температуре Т = 0К равна нулю.
- 9. Критерий самопроизвольного протекания процесса в закрытых системах. Энергия Гиббса. ΔH = ∆U + p∆V Q =
- 10. Критерий самопроизвольного протекания процесса в закрытых системах. Энергия Гиббса. Энергия Гиббса (обозначение ΔG) - это функция
- 11. Критерий самопроизвольного протекания процесса в закрытых системах. Энергия Гиббса. Самопроизвольно в закрытых системах (при p, T=Const)
- 12. Изменение энергии Гиббса в ходе химических реакций. В биохимии процессы, сопровождающиеся уменьшением энергии Гиббса (ΔG 0)
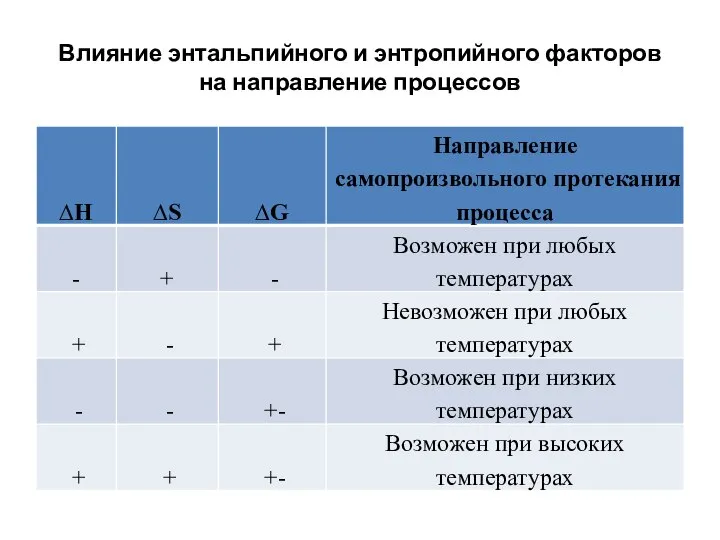
- 13. Влияние энтальпийного и энтропийного факторов на направление процессов
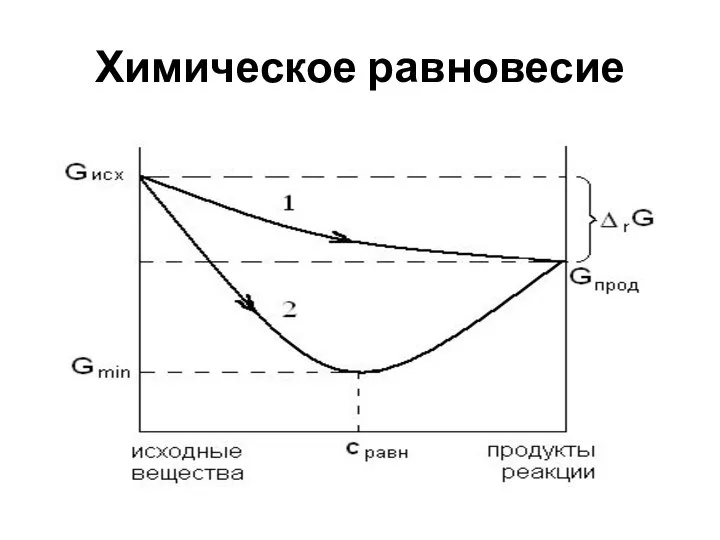
- 14. Химическое равновесие Химическое равновесие – это устойчивое, динамическое состояние системы, характеризующееся постоянством параметров состояния при постоянстве
- 15. Химическое равновесие
- 16. Химическое равновесие ΔG°r = - RT ln K - ΔG°r/ RT К = е ;K =
- 17. Константа равновесия – критерий направления процесса При ΔG ° > 0 K при ΔG° 1; при
- 18. Химическое равновесие aA + bB ⇔ dD + eE ΔGf(A)=ΔG°f(A)+RTlnCa(A) … уравнение изотермы Вант – Гоффа
- 19. Химическое равновесие в состоянии равновесия ΔGr= 0
- 20. ΔGr = - RT lnK + RT lnПс или: Пс > K ΔGr > 0 ←
- 21. Смещение равновесия ΔН>0 ΔН Влияние температуры Изобара Вант – Гоффа
- 23. Скачать презентацию

















 Шухов Владимир Григорьевич (1853–1939)
Шухов Владимир Григорьевич (1853–1939) Галогены
Галогены Кислород (Лекция 7)
Кислород (Лекция 7) Физические свойства металлов
Физические свойства металлов Творческий отчет кружка Юные химики
Творческий отчет кружка Юные химики Схема реакций
Схема реакций Индиго-краситель
Индиго-краситель Химия окислительновосстановительные реакции
Химия окислительновосстановительные реакции Азот и его соединения
Азот и его соединения Лабораторное оборудование. Тесты
Лабораторное оборудование. Тесты Природные источники углеводородов
Природные источники углеводородов Процессы переработки нефти
Процессы переработки нефти Презентация по Химии "Строении атомов. Химическая связь"
Презентация по Химии "Строении атомов. Химическая связь"  Спирты
Спирты Химический диктант по органической химии. 9 класс
Химический диктант по органической химии. 9 класс Презентация на тему Алкины
Презентация на тему Алкины  Урок по теме Алюминий .Строение.Свойства. Учитель: Деревянко Н.Г.
Урок по теме Алюминий .Строение.Свойства. Учитель: Деревянко Н.Г. Ионная полимеризация
Ионная полимеризация Кислотно-основные равновесия в растворах
Кислотно-основные равновесия в растворах Органическая химия. Теория строения органических веществ
Органическая химия. Теория строения органических веществ Кислород O2
Кислород O2 Промышленное производство азотных удобрений
Промышленное производство азотных удобрений Вода - самое удивительное вещество в природе. (8 класс)
Вода - самое удивительное вещество в природе. (8 класс) Генетическая связь между классами неорганических соединений
Генетическая связь между классами неорганических соединений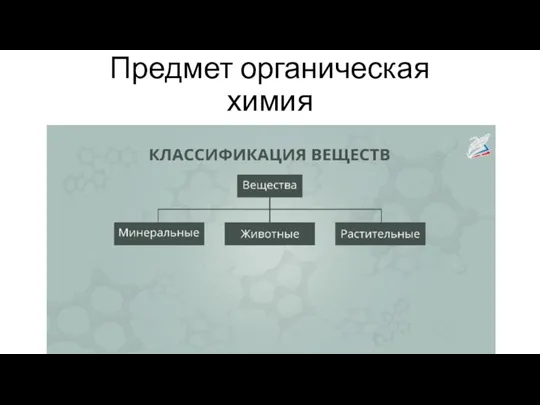 Органическая химия
Органическая химия Презентация на тему Правила безопасности труда в кабинете химии
Презентация на тему Правила безопасности труда в кабинете химии  Изучение микроклимата коровника с целью создания системы очистки воздуха от аммиака
Изучение микроклимата коровника с целью создания системы очистки воздуха от аммиака Презентация на тему Стекло
Презентация на тему Стекло