Содержание
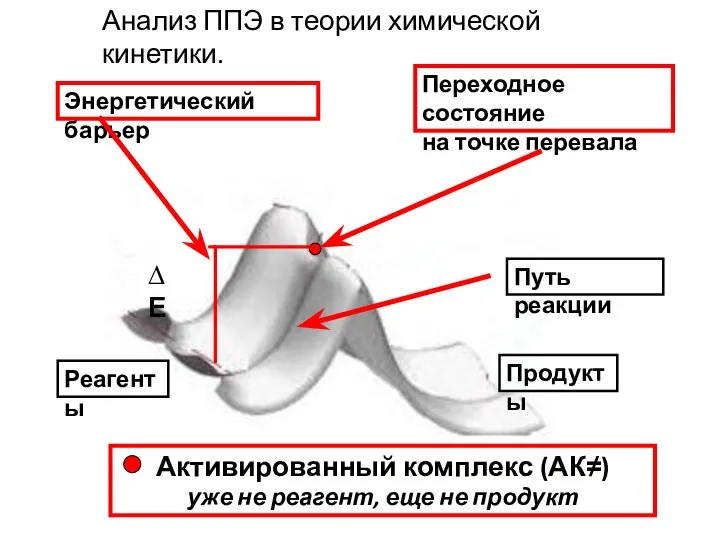
- 2. Переходное состояние на точке перевала Анализ ППЭ в теории химической кинетики. Энергетический барьер Продукты Активированный комплекс
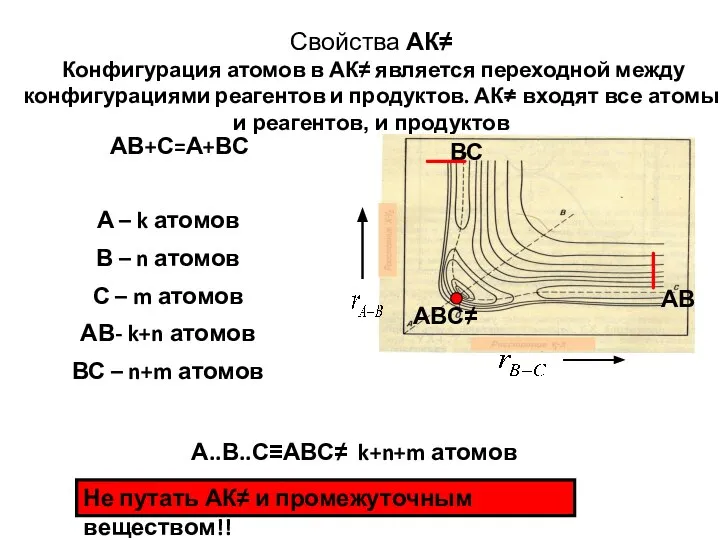
- 3. Свойства активированного комплекса (АК≠) Конфигурация атомов в АК≠ является переходной между конфигурациямми реагентов и продуктов. АК≠
- 4. Свойства АК≠ Конфигурация атомов в АК≠ является переходной между конфигурациями реагентов и продуктов. АК≠ входят все
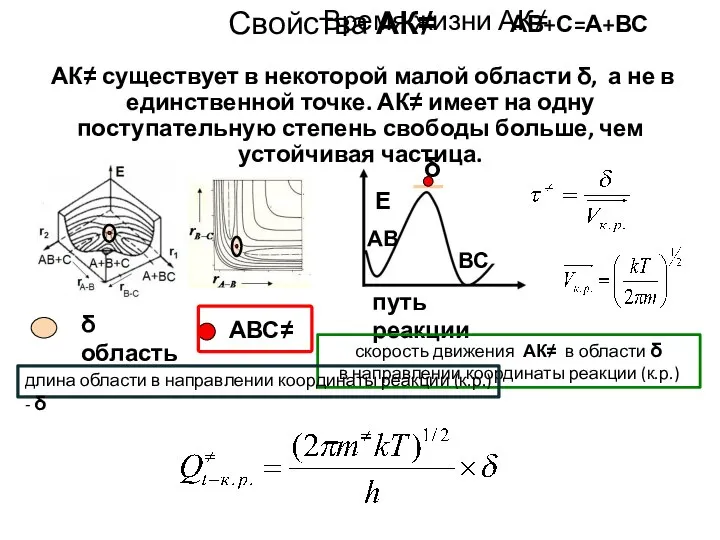
- 5. Свойства АК≠ АК≠ существует в некоторой малой области δ, а не в единственной точке. АК≠ имеет
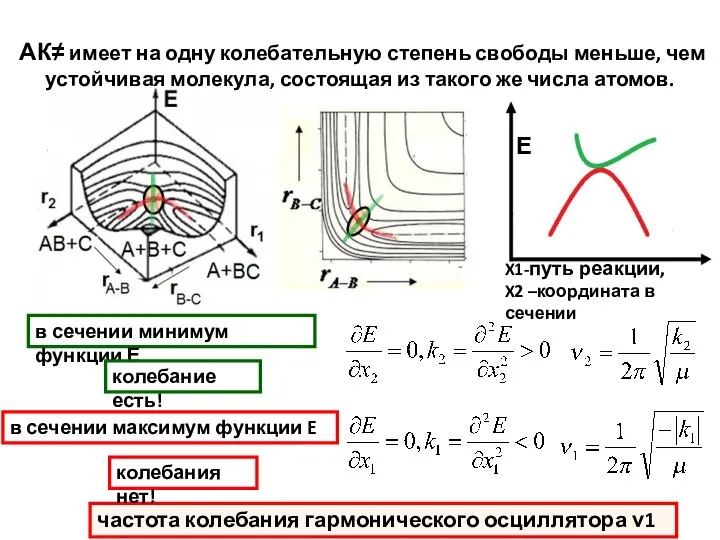
- 6. АК≠ имеет на одну колебательную степень свободы меньше, чем устойчивая молекула, состоящая из такого же числа
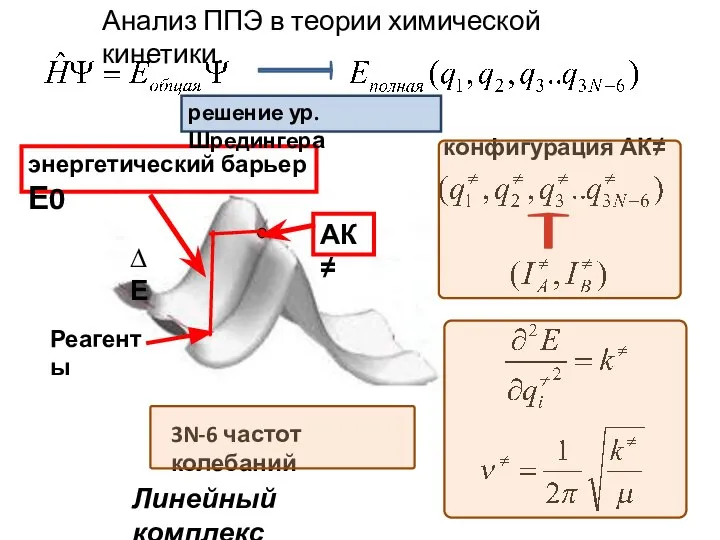
- 7. АК≠ Анализ ППЭ в теории химической кинетики. энергетический барьер Е0 Реагенты конфигурация АК≠ решение ур. Шредингера
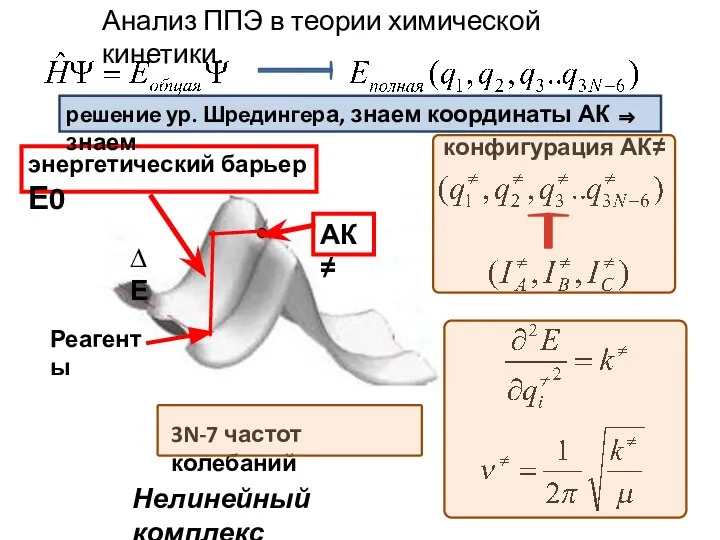
- 8. АК≠ Анализ ППЭ в теории химической кинетики. энергетический барьер Е0 Реагенты конфигурация АК≠ решение ур. Шредингера,
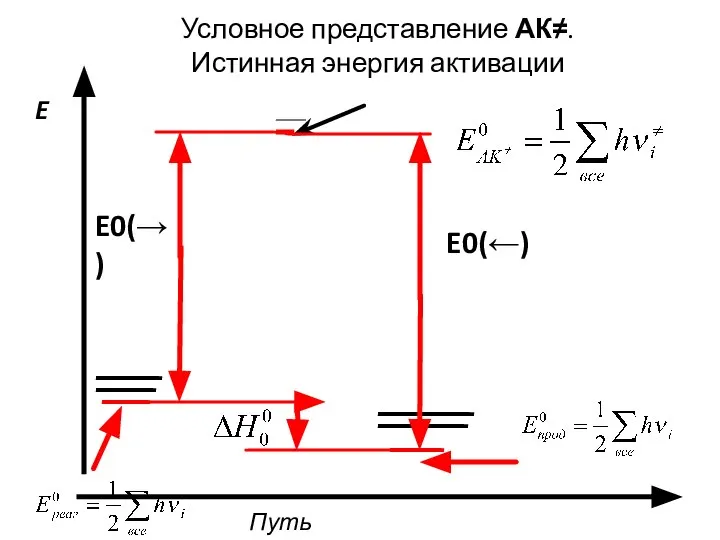
- 9. E0(←) Путь реакции E Условное представление АК≠. Истинная энергия активации E0(→)
- 10. Основные положения ТАК и кинетическая схема 1. Элементарный акт химического превращения протекает по пути наименьшей энергии.
- 11. Кинетическая схема ТАК и константа скорости Статистическое равновесие!! Не динамическое
- 12. Вывод выражения для константы скорости ТАК для реакции первого порядка поступательная степень свободы по координате реакции
- 13. Вывод выражения для константы скорости ТАК
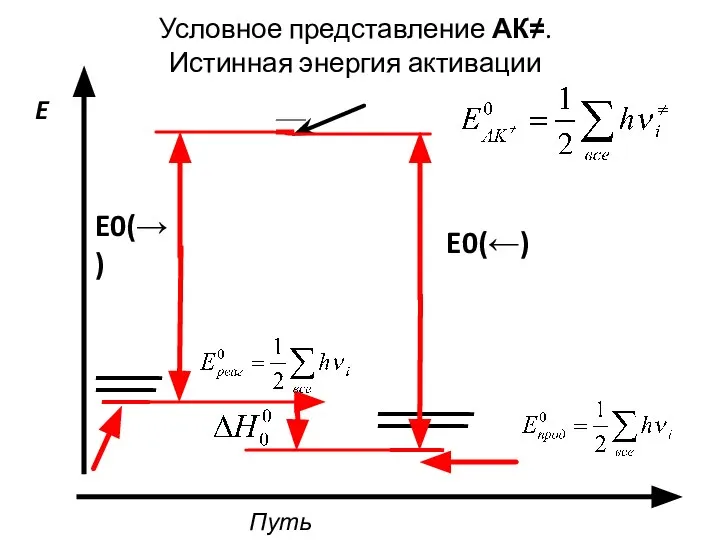
- 14. E0(←) Путь реакции E Условное представление АК≠. Истинная энергия активации E0(→)
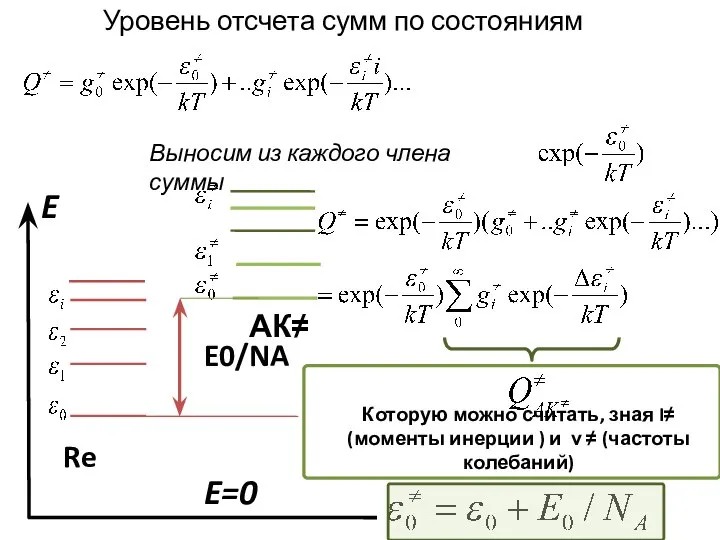
- 15. Уровень отсчета сумм по состояниям реагентов Re E E=0 Выносим из каждого члена суммы Которую можно
- 16. Которую можно считать, зная I≠ (моменты инерции ) и ν ≠ (частоты колебаний) Уровень отсчета сумм
- 17. Расчет kТАК
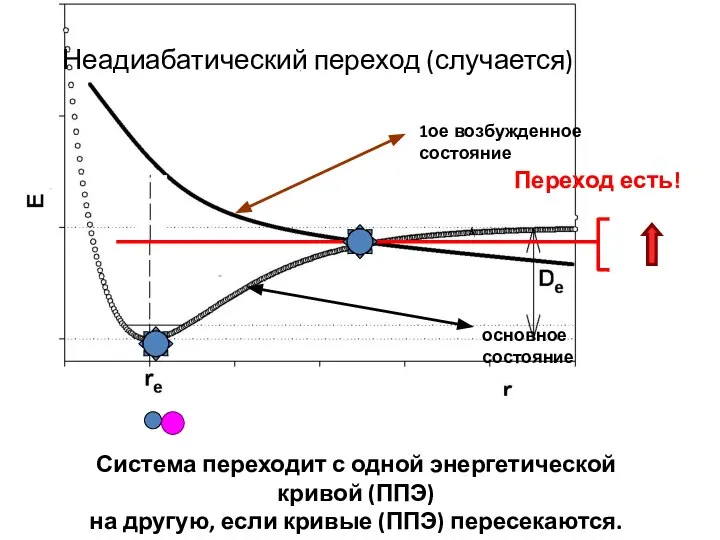
- 18. Неадиабатический переход (случается) 1ое возбужденное состояние основное состояние Система переходит с одной энергетической кривой (ППЭ) на
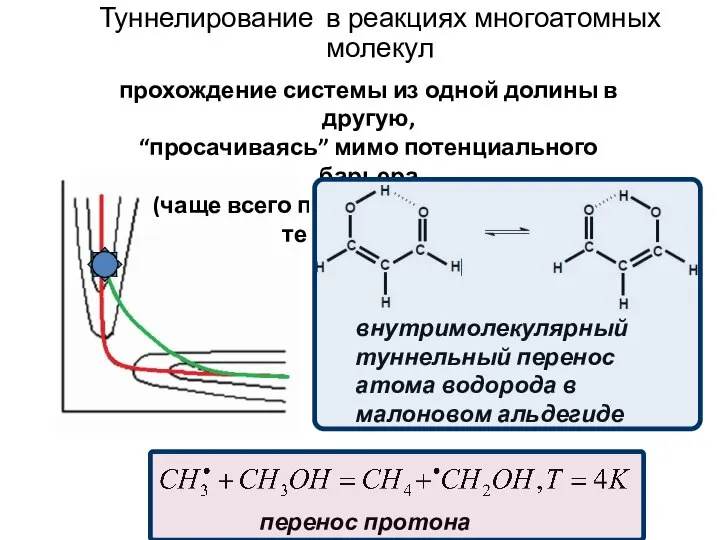
- 19. Туннелирование в реакциях многоатомных молекул прохождение системы из одной долины в другую, “просачиваясь” мимо потенциального барьера
- 20. Учет возможности туннелирования и неадиабатических переходов трансмиссионный коэффициент если случается туннелирование если случаются неадиабатические переходы
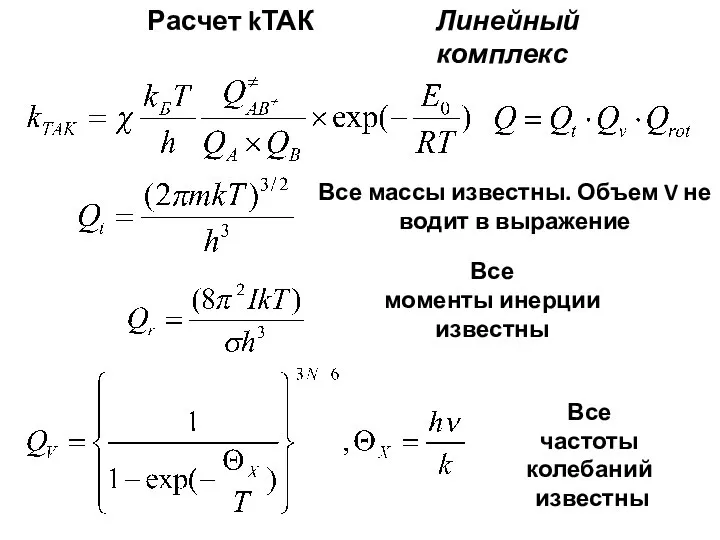
- 21. Расчет kТАК Все массы известны. Особенность – объем V не водит в выражение поступательной суммы по
- 22. Расчет kТАК Все массы известны. Объем V не водит в выражение Все частоты колебаний известны Все
- 23. После расчета ППЭ известны - координаты минимумов и седловой точки - высота барьера для перехода от
- 25. Скачать презентацию










 Великий кислород
Великий кислород Фенол. Физические свойства
Фенол. Физические свойства Мемо-химия. Защита проекта
Мемо-химия. Защита проекта Периодический закон. Периодическая таблица химических элементов. 8 класс
Периодический закон. Периодическая таблица химических элементов. 8 класс Классификация органических соединений
Классификация органических соединений Основы переработки нефти и нефтепродуктов
Основы переработки нефти и нефтепродуктов Неорганические вещества
Неорганические вещества Электролиз
Электролиз Ковалентная связь. Электроотрицательность
Ковалентная связь. Электроотрицательность Презентация на тему Предельные одноатомные спирты
Презентация на тему Предельные одноатомные спирты  Презентация на тему Водород (8 класс)
Презентация на тему Водород (8 класс)  Химиялық фармацевтикалық техниканың үдерістері
Химиялық фармацевтикалық техниканың үдерістері Термодинамическое равновесие между фазами
Термодинамическое равновесие между фазами Полимеры в медицине
Полимеры в медицине Основы химической термодинамики
Основы химической термодинамики Железо как химический элемент
Железо как химический элемент Простые эфиры и перекиси
Простые эфиры и перекиси Витамины. Способы получения
Витамины. Способы получения Химическая кинетика. Экзаменационные вопросы
Химическая кинетика. Экзаменационные вопросы Хроматометрия. Метод
Хроматометрия. Метод Основания. 8 класс
Основания. 8 класс Ароматические углеводороды. Бензол
Ароматические углеводороды. Бензол Периодическая система химических элементов. Им. Д.И. Менделеева
Периодическая система химических элементов. Им. Д.И. Менделеева Повторение классов соединений. Составление формул по названиям
Повторение классов соединений. Составление формул по названиям Исследование физико-химических свойств растворов сахарозы
Исследование физико-химических свойств растворов сахарозы Окислительно=восстановительное титрование
Окислительно=восстановительное титрование Изучение возможности синтеза порошка сложного карбонитрида -титана молибдена Ti-Mo в режиме СВС
Изучение возможности синтеза порошка сложного карбонитрида -титана молибдена Ti-Mo в режиме СВС Кислород
Кислород