Физика твердого тела. Введение в кристаллографию. Построение стереографических проекций

Базисные вектора – тройка некомпланарных векторов, соединяющих один из узлов решётки с тремя другими.
Параллелепипед, построенный на базисных векторах – элементарная ячейка пространственной решётки
Все возможные типы решеток, существующие в природе, представлены в таблице:

КРИСТАЛЛОГРАФИЧЕКИЕ ИНДЕКСЫ
УЗЛОВ, НАПРАВЛЕНИЙ, ПЛОСКОСТЕЙ
Узлы, направления и плоскости в кристаллической решётке принято обозначать тройками чисел
Индексы узла представляют собой его координаты, выраженные в единицах параметров решётки. Индексы узлов заключают в двойные квадратные скобки или приводят без скобок: [[001]] или 001.

Индексы направления, проходящего через начало координат, принимают координаты первого узла, лежащего на этом направлении. Индексы направлений заключают в одинарные квадратные скобки: [111]. Если какой-либо из индексов отрицателен, то минус ставят над цифрой.
Индексы направления всегда представляют собой три взаимно простых целых числа: пишут не [0 1 ½], а [0 2 1], не [224], а [112].
Если направление не проходит через нулевой узел, то нужно перенести (параллельным переносом) либо начало координат так, чтобы оно лежало на направлении, либо само направление так, чтобы оно проходило через начало координат.

Индексами плоскости, не проходящей через начало координат, являются числа, обратные величинам отрезков, которые плоскость отсекает на координатных осях.
Индексы плоскости заключают в круглые скобки. Если плоскость параллельна одной из осей («пересекается в бесконечности»), то соответствующий индекс равен нулю (1/∞= 0).
Если начало координат лежит в плоскости, то либо саму плоскость, либо нулевой узел необходимо перенести так, чтобы она не проходила через него.

Как и для направлений, индексы плоскостей всегда приводят к трём наименьшим (взаимно простым) целым числам.

При перемещении начала координат в другой узел решётки индексы всех остальных узлов изменяются, а индексы направлений и плоскостей остаются неизменными. Иначе говоря, тройка индексов задаёт не одну прямую или плоскость, а всё множество параллельных прямых (плоскостей) кристалла.
Некоторые непараллельные плоскости и направления являются тем не менее кристаллографически эквивалентными. Например, все рёбра элементарной ячейки кубической сингонии физически идентичны, хотя имеют разные индексы: [100], [010] и [001]; то же можно сказать и о её гранях (100), (010) и (001).
Совокупность кристаллографически эквивалентных направлений или плоскостей называется семейством. Индексы семейства направлений заключают в угловые скобки: а семейства плоскостей — в фигурные: {100}.

СТЕРЕОГРАФИЧЕСКИЕ ПРОЕКЦИИ НАПРАВЛЕНИЙ
За плоскость стереографической проекции Q принимается экваториальная плоскость, на которую сфера проецируется в виде круга проекций (рис.4). В результате пересечения сферической поверхность с Q имеем большой круг, отвечающий экватору сферы проекций и представляющий круг проекций.
Вертикальный диаметр шара NS, перпендикулярный к Q, называется осью проекций. Такая ось пересекает сферу проекций в двух точках N и S. Одна из этих точек (южный полюс S) является точкой зрения (“глазной точкой”).
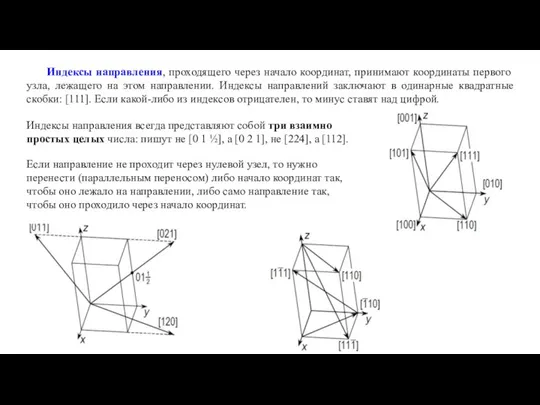
Рассмотрим построение стереографической проекции некоторого направления ОА: продолжим данное направление до пересечения со сферой проекций (точка а1). Соединим точку а1 с точкой зрения S лучом зрения Sа1. Точка а – точка пересечения Sа1 с плоскостью Q является стереографической проекцией направления ОА.
Если направление пересекает сферу проекций в ее нижний части, то за глазную точку принимается N (северный полюс). Таким образом, стереографические проекции направлений изображаются точками.