Основы программирования. Поиск на графах

Обход графа: поиск в глубину
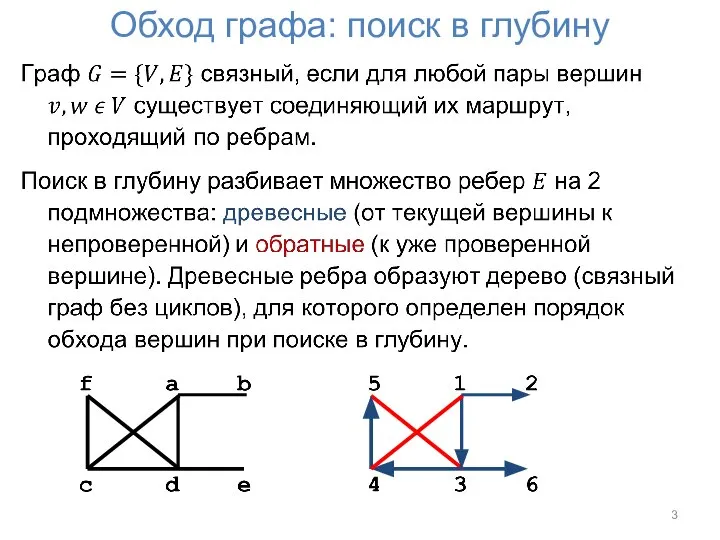
Поиск в глубину позволяет обойти все вершины графа по одному разу, переходя от вершины к вершине по ребрам.
Поиск в глубину реализуется рекурсивным алгоритмом:
Пусть выбрана некоторая не рассмотренная ранее вершина A
Перебираем все исходящие из A ребра, при этом:
если ребро ведет в не рассмотренную ранее вершину B, то продолжаем поиск рекурсивно от B
после обработки B возвращаемся в A и продолжаем перебирать исходящие из A ребра
если все ребра из A проверены, то либо возвращаемся к вершине, из которой мы пришли в A (если такая есть), либо выбираем любую ранее не проверенную вершину и выполняем алгоритм от нее.

Обход графа: поиск в глубину

Классы MGraph и LGraph
Будем добавлять методы к классам MGraph (матрица смежности) и LGraph (списки смежных вершин):
class MGraph
{
bool **mat; // матрица смежности
int vernum; // число вершин
…
};
class LGraph
{
List *lst; // списки смежных вершин
int vernum; // число вершин
…
};

Методы MGraph для поиска в глубину
Формируется массив R[0…n-1], где R[i] – номер вершины i в порядке обхода в глубину (от 1).
void MGraph::deep(int cver, int *R, int &cnum)
{
R[cver] = ++cnum;
for (int i = 0; i < vernum; i++)
if (mat[cver][i] && !R[i]) deep(i, R, cnum);
}
int* MGraph::DFS()
{
int i, cnum, *R = new int[vernum];
for (i = 0; i < vernum; i++) R[i] = 0;
for (cnum = i = 0; i < vernum; i++)
if (!R[i]) deep(i, R, cnum);
return R;
}

Метод deep для LGraph

Компоненты связности
Компоненты связности неориентированного графа это максимальные (по включению вершин) связные подграфы.
Для выделения компонент связности используем поиск в глубину, внеся следующие изменения:
добавим в класс MGraph целую переменную comptotal, в которой будет вычисляться число компонент
изменим процесс формирования массива R: R[i] будет хранить номер компоненты (от 1), включающую вершину i (R[i]=0, если вершина i еще не просмотрена).
Приводимые далее методы cdeep и get_comp – это модификации методов deep и DFS.

Методы MGraph для выделения компонент
void MGraph::сdeep(int cver, int *R)
{
R[cver] = comptotal;
for (int i = 0; i < vernum; i++)
if (mat[cver][i] && !R[i]) cdeep(i, R);
}
int* MGraph::get_comp()
{
int i, *R = new int[vernum];
comptotal = 0;
for (i = 0; i < vernum; i++) R[i] = 0;
for (i = 0; i < vernum; i++)
if (!R[i])
{ comptotal++; cdeep(i, R); }
return R;
}

Обход графа: поиск в ширину
Поиск в ширину обычно используется для проверки, существует ли маршрут из некоторой вершины-источника v в целевую вершину w, проходящий по ребрам графа.
В процессе поиска вершины помещаются в очередь для просмотра. Начальная очередь содержит только v.
Пусть u – текущая извлекаемая из очереди вершина.
Рассмотрим все ребра (u,x), при этом возможны варианты:
x просмотрена или находится в очереди – изменений нет,
x=w – маршрут найден, алгоритм завершается
x добавляется в очередь.
Если w не найдена, то после обработки всех ребер (u,x) из очереди выбирается следующая текущая вершина u, и поиск продолжается.
Если очередь закончилась, то маршрута из v в w нет.

Обход графа: поиск в ширину
При поиске в ширину можно не только определить, существует ли маршрут из v в w, но и вычислить его минимальную длину (минимальное число пройденных ребер). Для этого нужно вычислять уровни просмотренных вершин (массив Lev[0…n-1]):
вершина-источник v имеет уровень 1, начальные значения для остальных вершин Lev[i]=0 (это означает, что вершина i еще не рассмотрена),
если Lev[u]=a, существует ребро (u,x) и Lev[x]=0, то для x устанавливается значение уровня Lev[x]=a+1,
если Lev[w]>0, то существует, по крайней мере, один маршрут, и кратчайший маршрут содержит Lev[w]-1 ребро.

Обход графа: поиск в ширину
Функции для поиска в ширину имеют 1 параметр – номер v (от 0) вершины-источника. Поиск закончится, когда будут просмотрены все вершины, достижимые из v.
Для всех вершин графа будем формировать и возвращать массив уровней вершин Lev.
Если в результате поиска Lev[w]=0 для некоторой вершины w, то w не достижима из v.
Для организации очереди используем класс IQueue (очередь целых чисел) из раздела «Структуры и классы».

Метод MGraph для поиска в ширину
int* MGraph::BFS(int v)
{
int u, x, *Lev = new int[vernum];
IQueue Que(vernum);
for (u = 0; u < vernum; u++) Lev[u] = 0;
Lev[v] = 1; Que.push(v);
for (u = Que.pop(); u >= 0; u = Que.pop())
for (x = 0; x < vernum; x++)
if (mat[u][x] && !Lev[x])
{
Lev[x] = Lev[u] + 1;
Que.push(x);
}
return Lev;
}

Метод LGraph для поиска в ширину
int* LGraph::BFS(int v)
{
int u, *px, *Lev = new int[vernum];
IQueue Que(vernum);
for (u = 0; u < vernum; u++) Lev[u] = 0;
Lev[v] = 1; Que.push(v);
for (u = Que.pop(); u >= 0; u = Que.pop())
for (px = lst[u].get_first();
px != NULL; px = lst[u].get_next())
if (!Lev[*px])
{
Lev[*px] = Lev[u] + 1;
Que.push(*px);
}
return Lev;
}

Выделение минимального остова

Выделение минимального остова

Выделение минимального остова

Выделение минимального остова

Выделение минимального остова

Алгоритм Прима

Алгоритм Прима

Алгоритм Прима

Метод WGraph для алгоритма Прима
void WGraph::get_span_tree() {
double wmin;
int i, j, vm, *B = new int[vernum];
B[0] = -1;
for (i = 1; i < vernum; i++) B[i] = 0;
for (i = 1; i < vernum; i++) {
wmin = MAX; vm = 0;
for (j = 1; j < vernum; j++)
if (B[j] != -1 && wmin > mat[j][B[j]])
{ vm = j; wmin = mat[j][B[j]]; }
if (!vm) return;
add_edge(vm, B[vm]); B[vm] = -1;
for (j = 1; j < vernum; j++)
if (B[j]!=-1 && mat[j][B[j]]>mat[j][vm])
B[j] = vm;
}
}

Алгоритм Крускала

Алгоритм Крускала

Быстрое объединение множеств

Быстрое объединение множеств
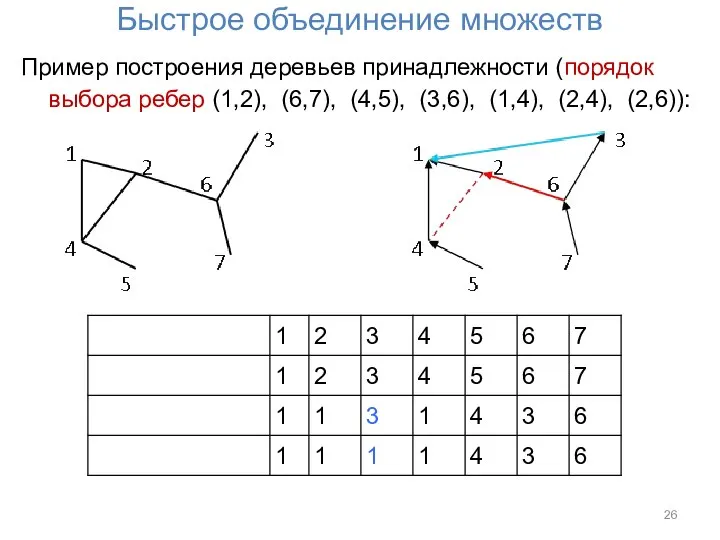
Пример построения деревьев принадлежности (порядок выбора ребер (1,2), (6,7), (4,5), (3,6), (1,4), (2,4), (2,6)):

Быстрое объединение множеств

Быстрое объединение множеств

Алгоритм Крускала для массива ребер
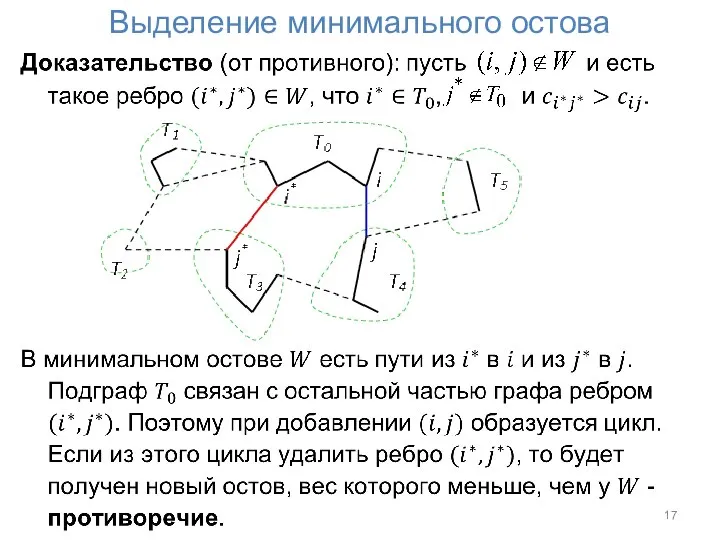
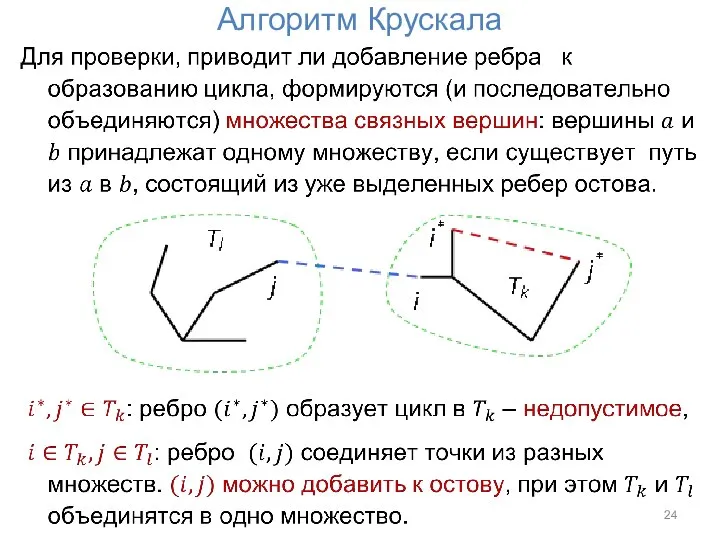
Алгоритм Крускала приводится в виде отдельной функции span_tree, которая выделяет минимальный остов графа, заданного массивом длины e взвешенных ребер R (число вершин равно n). Остов сохраняется в массиве W длины n-1, который также содержит взвешенные ребра и должен быть выделен заранее. span_tree выделяет остов и возвращает число его ребер (<= n-1).
Взвешенное ребро представляется структурой
struct Edge
{
int a, b; // номера двух вершин ребра
double weight; // вес ребра (для сортировки)
}
Функция sort_edges производит сортировку массива R по возрастанию весов ребер.

Алгоритм Крускала для массива ребер
int span_tree(Edge *R, int e, int n, Edge *W)
{
int k = 0, ra, rb, i, *A, *B;
A = new int[n]; B = new int [n];
sort_edges(R, e);
for (i=0; i < n; i++) { A[i] = i; B[i] = 1; }
for (i = 0; k < n-1 && i < e; i++) {
for (ra = R[i].a; ra != A[ra]; ra = A[ra]);
for (rb = R[i].b; rb != A[rb]; rb = A[rb]);
if (ra == rb) continue;
W[k++] = R[i];
if (B[ra] >= B[rb])
{ A[rb] = ra; B[ra] += B[rb]; }
else { A[ra] = rb; B[rb] += B[ra]; }
} return k;
}