Регрессионный анализ. Линейная регрессионная модель

Если расчёт коэффициентов корреляции характеризует силу связи между двумя переменными, то регрессионный анализ служит для определения вида этой связи и дает возможность для прогнозирования значения одной (зависимой) переменной отталкиваясь от значения другой (независимой) переменной. Регрессионные модели: линейная и множественная.

Линейная регрессионная модель
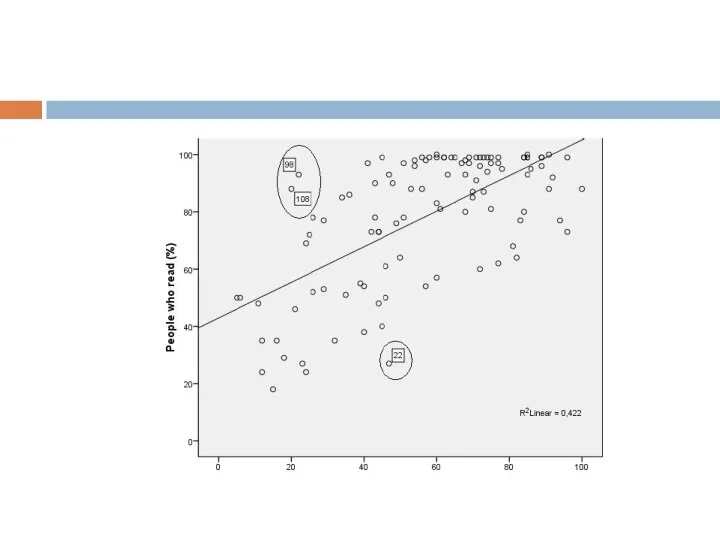
Прежде чем приступать к построению регрессионной модели обратимся к диаграмме рассеивания, она поможет нам визуально оценить наличие линейной связи и выявить выбросы, которые могут существенно повлиять на результаты построенной модели.
Для того чтобы построить диаграмму рассеивания выполним команду Graphs→Legacy Dialogs→Scatter/Dot и выбираем построение простой диаграммы (Simple Scatter). В появившемся окне расставляем наши переменные по осям координат: х ‐ независимая переменная, у ‐ зависимая переменная. В Output появляется наш график, на который нам необходимо нанести прямую. Для этого дважды щелкаем левой кнопкой мыши по графику и в появившемся окне, на графике, щелкаем правой кнопкой мыши и выбираем вторую строчку снизу Add Fit Line at Total.

На графике мы можем наблюдать линейную зависимость между переменными, а, следовательно, приступить к построению линейной регрессии. Однако мы можем наблюдать три выброса, которые, возможно, могут повлиять на конечный результат (для того, чтобы узнать номера выбросов, в том же окне где мы рисовали прямую, кнопкой в виде мишени нажимаем на интересующие нас случаи). После построения регрессионной модели мы можем попробовать убрать наши выбросы из базы посредством фильтрации и еще раз построить регрессионную модель.

И последнее что необходимо проверить перед построением регрессионной модели это нормальность распределения наших переменных (это необходимо только для интервальных шкал). Чтобы это сделать нам необходимо провести тест Колмогорова‐Смирнова или Шапиро‐Уилка для выборки меньше 50. Выполним команду Analyze→Descriptive Statistics→Explore. Добавляем наши переменные в Dependend list и не забываем отметить во вкладке Plots галочку напротив Histogram, это позволит визуализировать распределение для переменных и напротив Normality plots with tests, это выведет нам тест Колмогорова‐Смирнова.

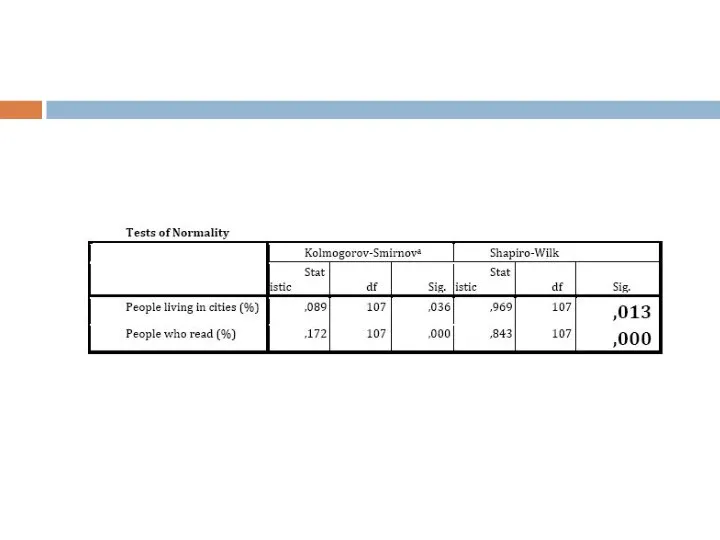
Для того чтобы интерпретировать полученные результаты сформулируем две гипотезы.
Н0: распределение значений переменной не отличается от нормального распределения
Н1: распределение отличается от нормального
Для того чтобы подтвердить нормальность распределения нам необходимо чтобы вероятность/значимость (sig.) была больше 0, 05. В нашем случае значимость меньше, поэтому мы делаем вывод о том, что распределение значимо отличается от нормального.

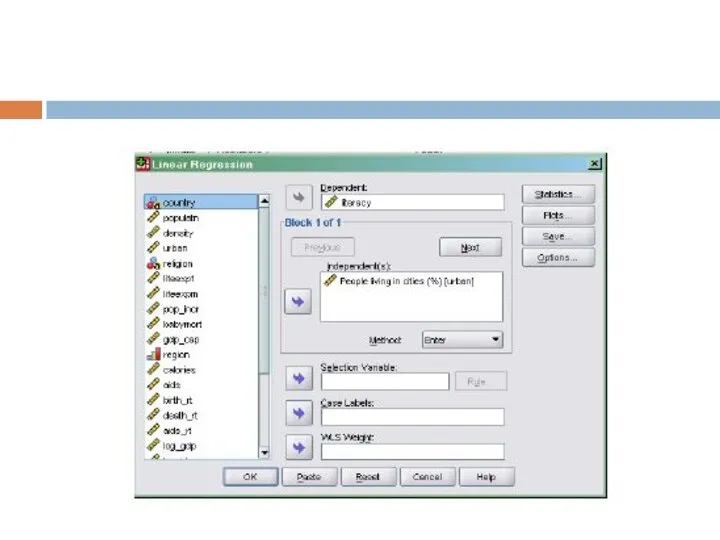
Теперь приступим к построению линейной регрессионной модели. Для того чтобы осуществить линейный регрессионный анализ необходимо выполнить команду Analyze→Regression→Linear Regression.

После добавления переменных заходим во вкладки. Во вкладке Save сохраняем предсказанные значения (Predicted Values‐ Unstandardized) и наши остатки (Residuals‐Standardized) и нажимаем ОК.
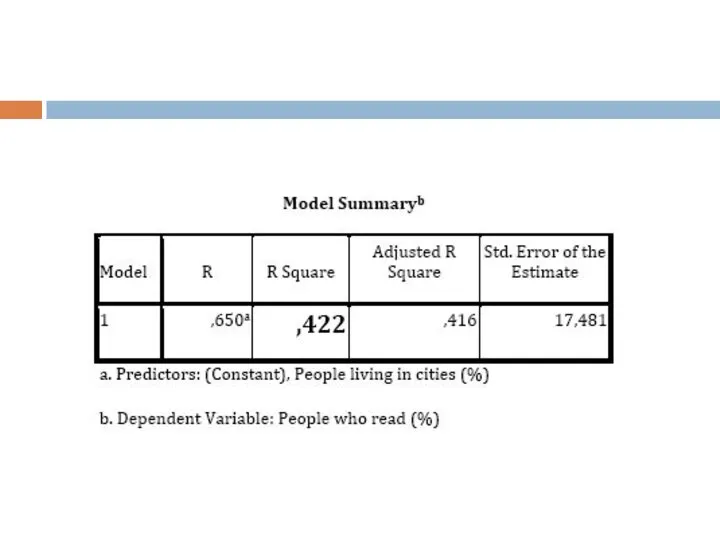
Теперь пришло время интерпретации результатов. В отчете мы получили несколько таблиц идем по порядку. В первой таблице мы смотрим на второй столбец R Square, который показывает нам качество регрессионной модели, в отличие от R, который представляет собой коэффициент корреляции между переменными. R2, лежит в диапазоне от 0 до 1, соответственно, чем он больше, тем наша регрессионная модель лучше и объясняет большое количество случаев. Интерпретировать регрессионную модель можно в том случае если она объясняет хотя бы 30% случаев и больше, то есть когда R2 больше или равен 0,3. При маленьком R2 дальнейшая интерпретация регрессионной модели является бессмысленной, поскольку предсказанные значения объясняют маленький процент случаев.

Итак, мы с вами видим, что наша модель неплохая, и объясняет 42% случаев. Казалось бы, все хорошо и на этом наша интерпретация может завершиться, однако нам необходимо убедиться в том, что наша модель значима, т.е. корреляционные связи между переменными являются значимыми. Для этого нам необходимо обраться ко второй таблице

Для того чтобы правильно интерпретировать результаты этой таблицы нам необходимо сформулировать гипотезы, как мы это делали для теста Колмогорова‐Смирнова. Здесь нас также интересует значимость 0,05, но в этот раз нам важно, чтобы она была ниже этого значения. В нашем случае она приближается к нулю, а, следовательно, мы можем говорить о том, что наша построенная модель статистически значима.
В таблице коэффициенты нас интересует статистическая значимость нашей переменной, так же как и в предыдущей таблице смотрим на значимость. Делаем вывод о том, что наша переменная является статистически значимой.

Таким образом, мы можем сделать вывод о том, что чем больше численность городского населения, тем больше количество читающих людей (R=0, 62). Наша модель получилась статистически значимой и объясняет 40% случаев. Однако следует помнить о том, что распределение наших переменных было ненормальным, поэтому предсказанные нами значения не могут приниматься однозначно.

Множественная регрессия
Множественная регрессия отличается от простой только количеством независимых переменных, поэтому порядок действий остается прежним. Зависимой переменной у нас будет процент городского населения (Sb), а независимыми переменными будут все оставшиеся (кроме переменной страна).

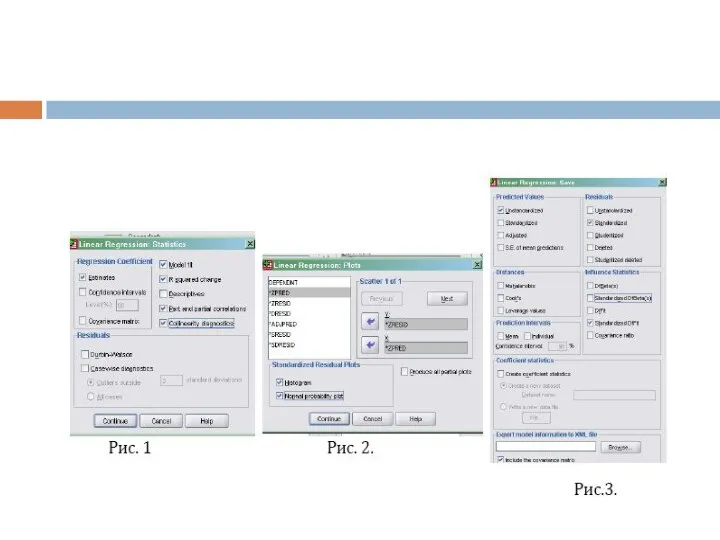
Самым важным действием на данном этапе является работа с вкладками. Итак, первая вкладка Statistics, в ней мы отмечаем галочками R2 и вывод корреляционных связей (см. Рис 1). Вкладка Plots построит нам диаграмму рассеивания, позволяющий нам визуально оценить гомо или гетероскедастичность, т.е. однородность или неоднородность наблюдений. По оси Y у нас распологаются остатки (ZRESID), по оси X предсказанные значения (ZPRED). Кроме того, наши остатки должны быть нормальными, поэтому попросим программу построить купол Гаусса (отметим две галочки внизу окна) (см. Рис.2). И наконец последняя вкладка Save, которая позволит нам сохранить наши стандартизированные остатки и предсказанные значения, а также статистики влияния, на основе которых мы сможем исключить сильно влияющие случаи (см. Рис.3)

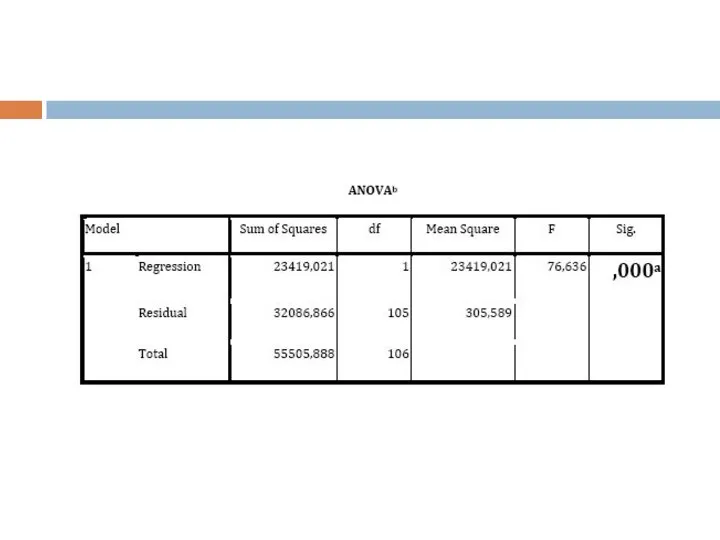
Интерпретация в целом ничем не отличается от того, что мы делали в простой модели. В первую очередь смотрим на R2, он равен 0,574, это говорит нам о том, что построенная нами модель объясняет 57% случаев. Таблица ANOVA показывает нам, что построенная нами модель является статистически значимой (Sig.=0,003, что меньше 0,05). Теперь смотрим на самую важную таблицу коэффициентов.

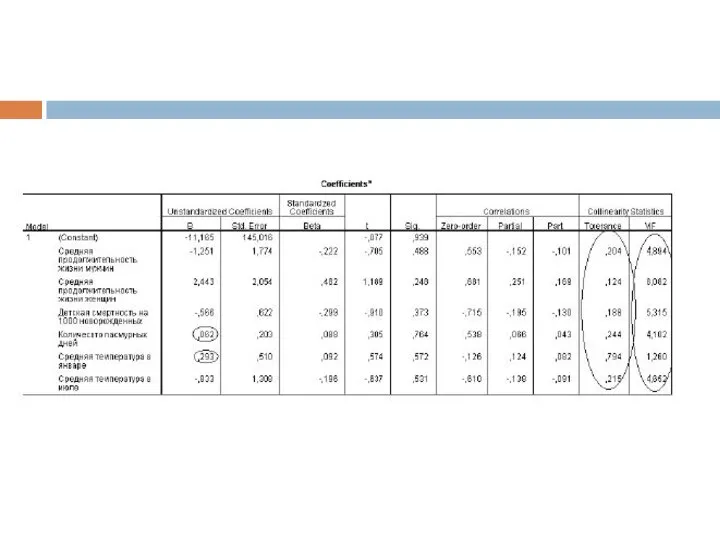
В первую очередь обращаем внимание на то, какие переменные наиболее важные, т.е. те, чьи значения высокие (столбец В). Как мы видим, есть две переменные, чьи значения практически приближаются к нулю и, следовательно, практически не влияют на нашу модель.

Поскольку в нашей модели несколько независимых переменных, то мы можем говорить о таком понятии как мультиколлинеарность, т.е. наличии корреляционных связей между независимыми переменными, что, в свою очередь, делает оценку уникальной роли каждой независимой переменной трудной или невозможной. В таблице с коэффициентами мы смотрим на статистики коллинеарности ‐ последний столбец (вывод этого столбца производится посредством вкладки Statistics). Обратимся к толерантности. Коэффициент толерантности показывает уровень мультиколлинеарности данной независимой переменной с другими. Правило большого пальца: на существование мультиколлинеарности указывает значение толерантности <0, 2. Чем ближе толерантность к нулю, тем выше мультиколлинеарность. Второе, что помогает нам выявить наличие мультиколлинеарности это анализ VIF (фактор инфляции дисперсии).

Данный показатель противоположен по смыслу толерантности, поэтому высокие значения VIF говорят нам о высокой мультиколлинеарности. Принято считать, что значения превышающие 4 указывают на проблемы мультиколлинеарности, однако некоторые ученые используют более мягкий критерий 10 в качестве данного показателя. Вы можете удалить из регрессионной модели переменную с высоким показателем мультиколлинеарности в том случае, если это не противоречит теоретическим ожиданиям. В нашем случае, мы можем удалить вторую и третью переменные, поскольку значение толерантности ниже 0, 2 и показатели VIF довольно высоки. Проблему мультиколлинеарности может решить факторный анализ, который соединяет переменные, измеряющие одинаковые показатели.

!!! Следует помнить, что если по каким то причинам мы не можем удалить наши переменные из регрессии и сама модель получилась неплохая в интерпретации результатов следует обратить особое внимание на наличие мультиколлинеарности и на то, что это может повлиять на предсказанную модель.

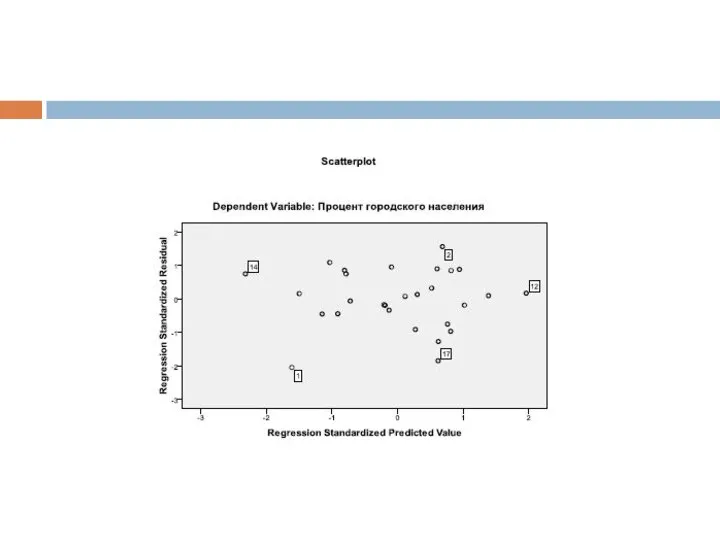
Теперь нам осталось оценить наши остатки на гомо или гетероскедастичность. Для этого мы построили диаграмму рассеивания. Хотелось бы обратить внимание на выбросы, которые возможно оказывают значительное влияние на конечную регрессионную модель. Эти случаи мы можем на время исключить из конечных выводов, однако помним о том, что удаление не должно противоречить нашим теоретическим ожиданиям. Купол гаусса нам также показывает, что полученные нами остатки отличаются от нормального распределения, однако мы можем заметить, что искажает весь график колонка слева, для того, чтобы посмотреть наличие влияющих наблюдений необходимо обратиться к сохраненным значениям (возвращаемся в основное окно на вкладку DataView).

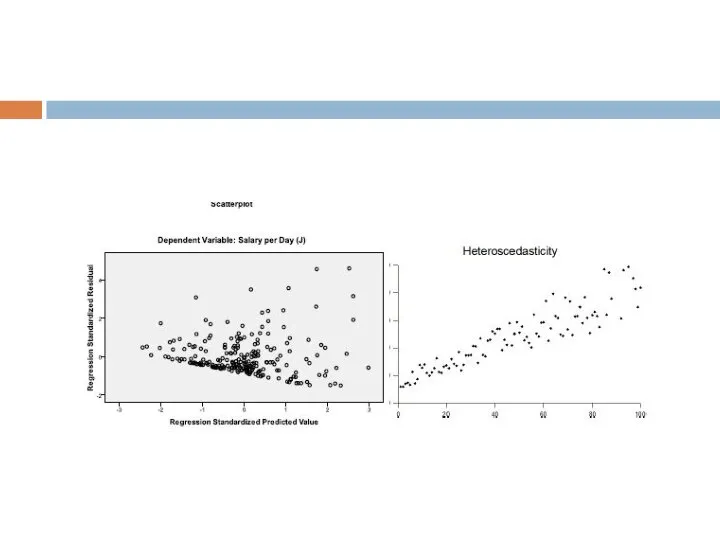
Смотря на диаграмму, мы можем говорить об однородности наблюдений, т.е. о гомоскедастичности (нет общей тенденции, наблюдения располагаются однородно по всей плоскости). Для примера приведем диаграмму рассеивания с гетероскедастичностью.