Объем прямой призмы

Цели урока:
Вспомнить понятие призмы.
Изучить теорему об объеме призмы.
Провести доказательство.
Применить полученные знания на практике.

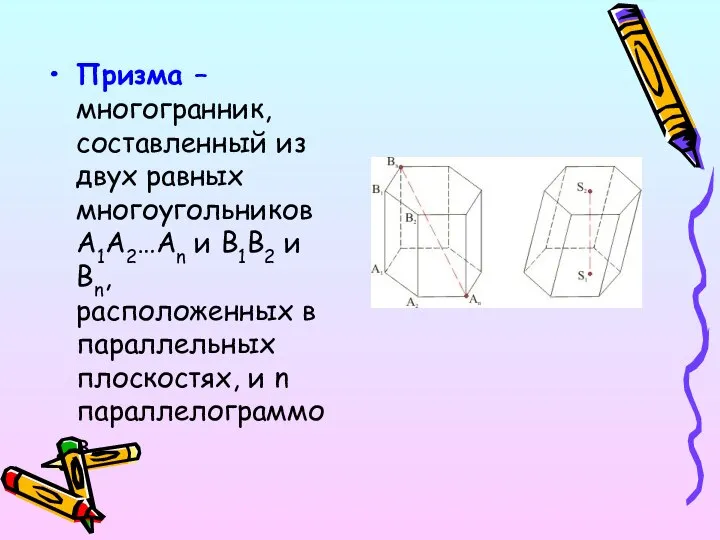
Призма – многогранник, составленный из двух равных многоугольников A1A2…An и B1B2 и Bn, расположенных в параллельных плоскостях, и n параллелограммов.

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой.
Прямая призма называется правильной, если её основания – правильные многоугольники.

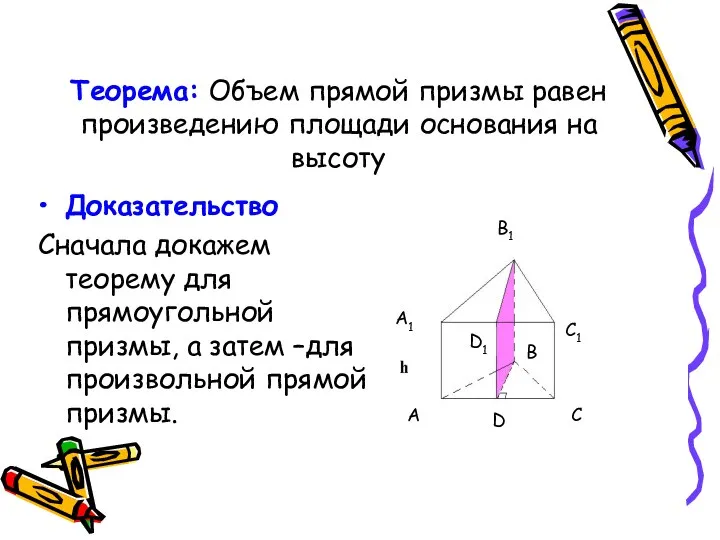
Теорема: Объем прямой призмы равен произведению площади основания на высоту
Доказательство
Сначала докажем теорему для прямоугольной призмы, а затем –для произвольной прямой призмы.
В
D1
А1
В1
С1
А
C
D

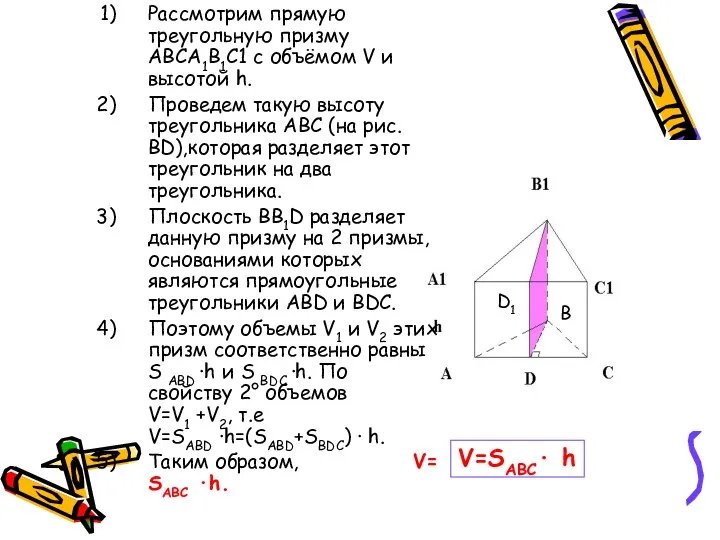
Рассмотрим прямую треугольную призму ABCA1B1C1 с объёмом V и высотой h.
Проведем такую высоту треугольника ABC (на рис. BD),которая разделяет этот треугольник на два треугольника.
Плоскость BB1D разделяет данную призму на 2 призмы, основаниями которых являются прямоугольные треугольники ABD и BDC.
Поэтому объемы V1 и V2 этих призм соответственно равны S ABD ·h и S BDC ·h. По свойству 2° объемов V=V1 +V2, т.е V=SABD ·h=(SABD+SBDC) · h.
Таким образом, V= SABC ·h.
V=SABC∙ h
В
D1

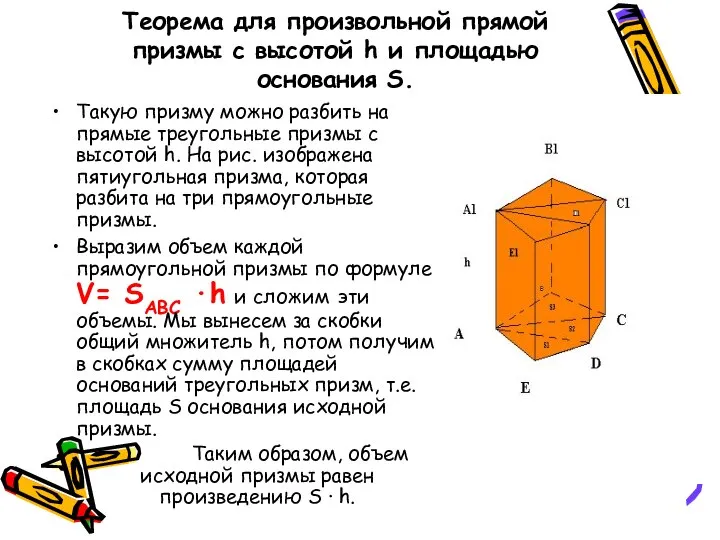
Теорема для произвольной прямой призмы с высотой h и площадью основания S.
Такую призму можно разбить на прямые треугольные призмы с высотой h. На рис. изображена пятиугольная призма, которая разбита на три прямоугольные призмы.
Выразим объем каждой прямоугольной призмы по формуле V= SABC ·h и сложим эти объемы. Мы вынесем за скобки общий множитель h, потом получим в скобках сумму площадей оснований треугольных призм, т.е. площадь S основания исходной призмы.
Таким образом, объем исходной призмы равен произведению S · h.

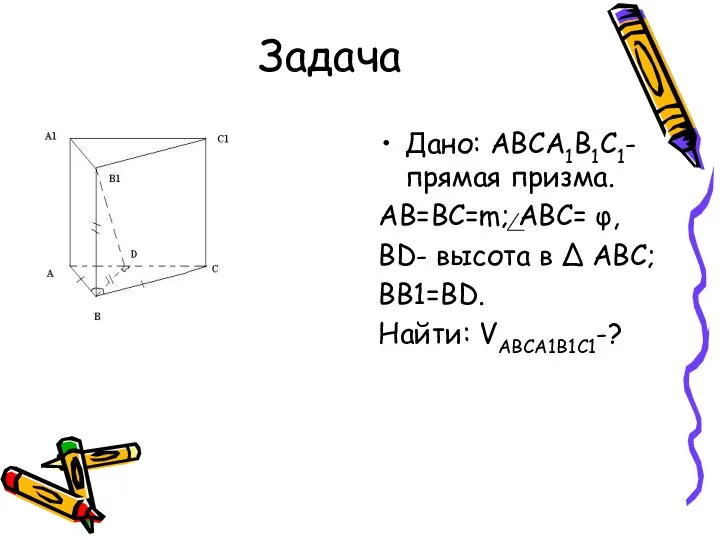
Задача
Дано: ABCA1B1C1- прямая призма.
AB=BC=m; ABC= φ,
BD- высота в ∆ ABC;
BB1=BD.
Найти: VABCA1B1C1-?

Решение:
S ABC ·h, h=BB1.
Рассмотрим ∆ ABC; ∆ ABC- р/б. BD- высота ∆ ABC, следовательно медиана и биссектриса.
ABD= DBC= φ/2
3) Рассмотрим ∆ ABD; ∆ ABD- прямоугольный. Из соотношения в ∆: cosφ/2 = BD/AB BD= cosφ/2 AB, BD=m cosφ/2 (AB=m)
4) Т.к. BD=BB1 BB1=m · cos φ /2
5) S ABC= ½ AB·BC· sinφ; S ABC= ½ m2 · sinφ
6) V= ½ m2 · sinφ· mcosφ/2=½ m3 · sinφ · cosφ/2
Ответ: ½ m3 · sinφ · cosφ/2

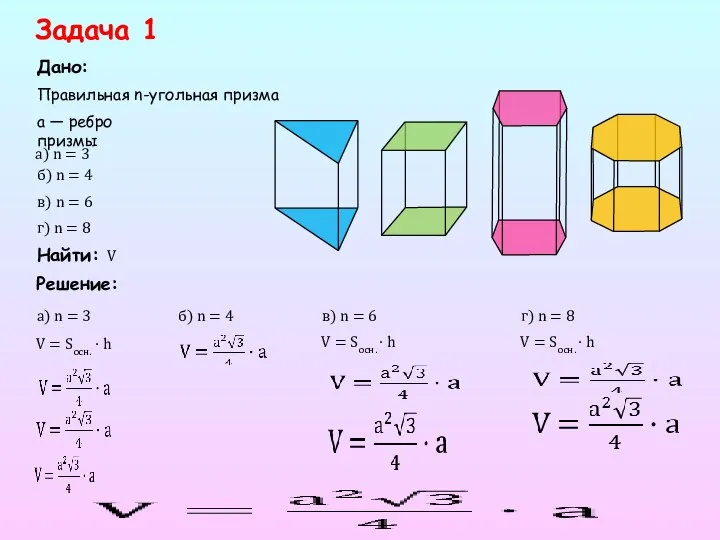
Задача 1
Дано:
Решение:
Найти: V
Правильная n-угольная призма
a) n = 3
а) n = 3
а — ребро призмы
б) n = 4
в) n = 6
V = Sосн. · h
г) n = 8
б) n = 4
V = Sосн. · h
в) n = 6
V = Sосн. · h
г) n = 8

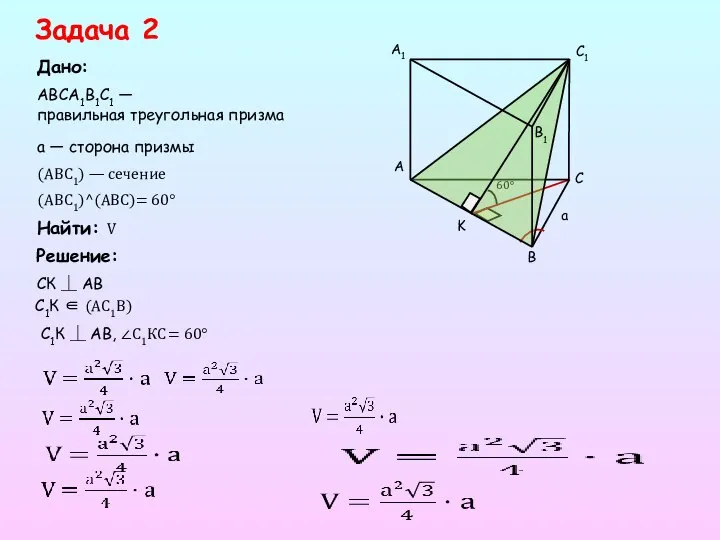
60°
Задача 2
Дано:
Решение:
Найти: V
АВСА1В1С1 —
правильная треугольная призма
СК ⏊ АВ
(ABC1) — сечение
а — сторона призмы
(ABC1)^(АВС)= 60°
С1К ⏊ АВ, ∠С1КС = 60°
A1
C1
B1
A
K
B
C
a
С1К ∈ (AC1B)