Задачи на обобщение изученного материала

б) CDD1, DA1C1, BDC1;
В кубе A…D1 укажите плоскости, проходящие через вершины куба, параллельные прямой: а) AA1; б) AB1; в) AC1.
Ответ: а) BCC1, CDD1, BDD1;
в) нет.
Упражнение 2

Докажите, что для куба ABCDA1B1C1D1 прямая AA1 параллельна плоскости BCC1.
Доказательство: Прямая AA1 параллельна прямой BB1, лежащей в плоскости BCC1. Следовательно, прямая AA1 параллельна плоскости BCC1.
Упражнение 3

Назовите прямые, содержащие многогранника, изображенного на рисунке, все плоские углы которого прямые, параллельные плоскости ABC.
Ответ. B1C1, A1D1, B2C2, A2D2, A1B1; C1D1; A2B2; C2D2.
Упражнение 4

Сколько имеется пар параллельных прямых и плоскостей, содержащих ребра октаэдра?
Решение: Для каждого ребра имеется две грани, ей параллельные. У октаэдра 12 ребер. Следовательно, искомое число пар параллельных прямых и плоскостей равно 24.
Упражнение 5*

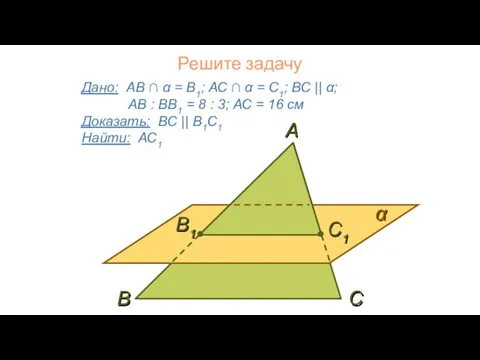
Решите задачу
Дано: АВ ∩ α = В1; АС ∩ α = С1; ВС || α;
АВ : ВВ1 = 8 : 3; АС = 16 см
Доказать: ВC || B1С1
Найти: АС1

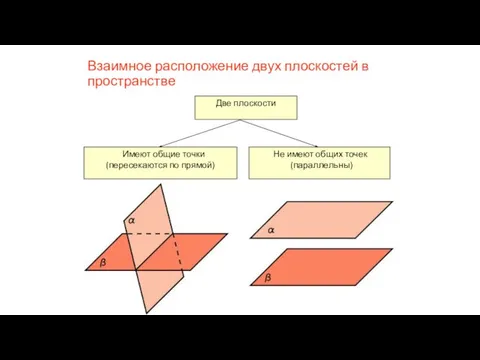
Определение. Две плоскости в пространстве называются параллельными, если они не имеют общих точек.
ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ
В ПРОСТРАНСТВЕ

Взаимное расположение двух плоскостей в пространстве

Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
Признак параллельности двух плоскостей
Доказательство. Пусть две пересекающиеся прямые a1, a2 плоскости α соответственно параллельны двум прямым b1, b2 плоскости β. Докажем, что плоскости α и β параллельны.

а) ABB1 и CDD1;
б) ABB1 и DEE1;
в) ABB1 и CEE1;
г) ABB1 и CFF1;
д) ABB1 и CFE1,
Ответ: а) Нет;
б) да;
в) нет;
г) да;
д) нет.
Являются ли параллельными плоскости:
Упражнение 6
проходящие через вершины правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 ?