склада за день можно приготовить в совокупности не более 700 изделий. Рабочий день длится 8 часов. Если выпускать только пирожные, за день можно произвести не более 250 штук, пирожков же можно произвести 1000, если при этом не выпускать пирожные. Стоимость пирожного вдвое выше, чем пирожка. Требуется составить дневной план производства, обеспечивающий кондитерскому цеху наибольшую выручку.
На изготовление одного пирожного затрачивается в 4 раза больше времени, чем на изготовление одного пирожка.
t – время изготовления одного пирожка (минут)
время изготовления x пирожков (минут)
tx
время изготовления y пирожных (минут)
4ty
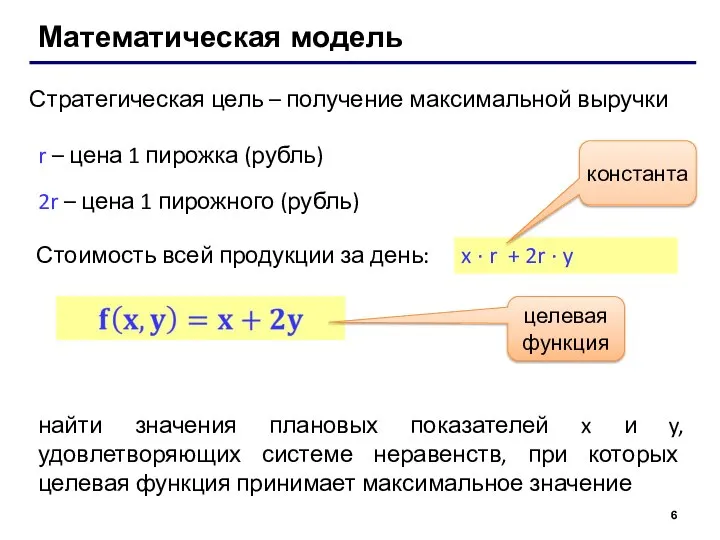
4ty + tx ≤ 480




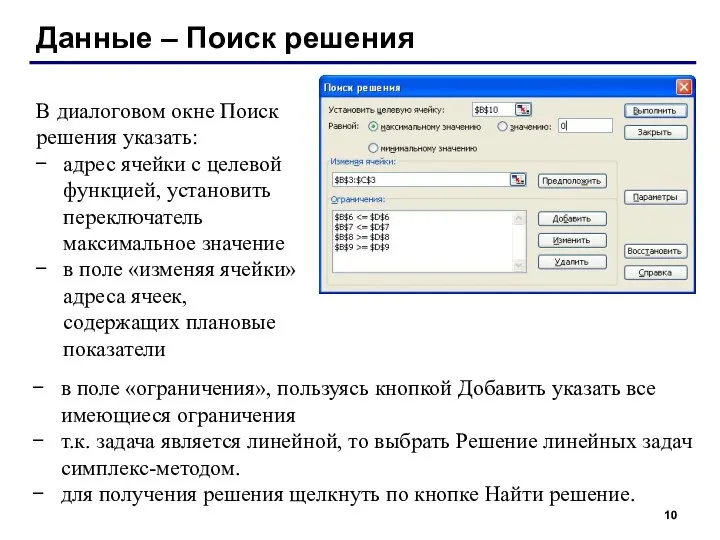
 Определенный интеграл
Определенный интеграл Цилиндр. История возникновения
Цилиндр. История возникновения Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика
Интерактивная игра для детей дошкольного возраста Путешествие в страну Математика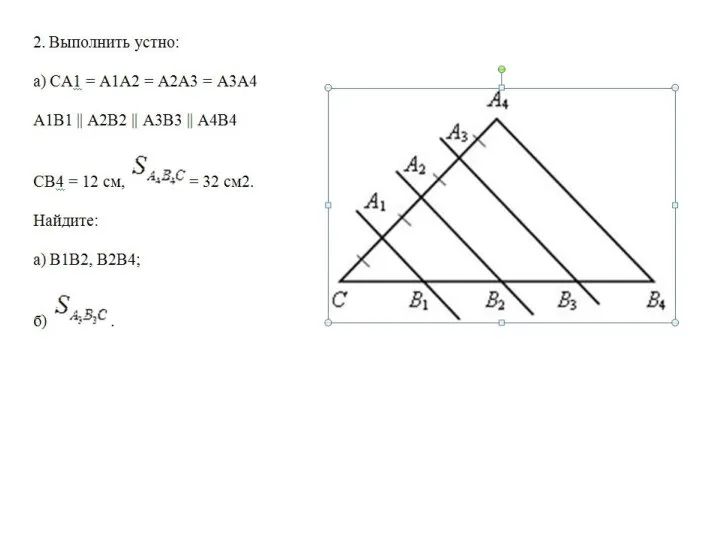 Признаки подобия треугольников. Урок 31
Признаки подобия треугольников. Урок 31 Приложения Определенного интеграла
Приложения Определенного интеграла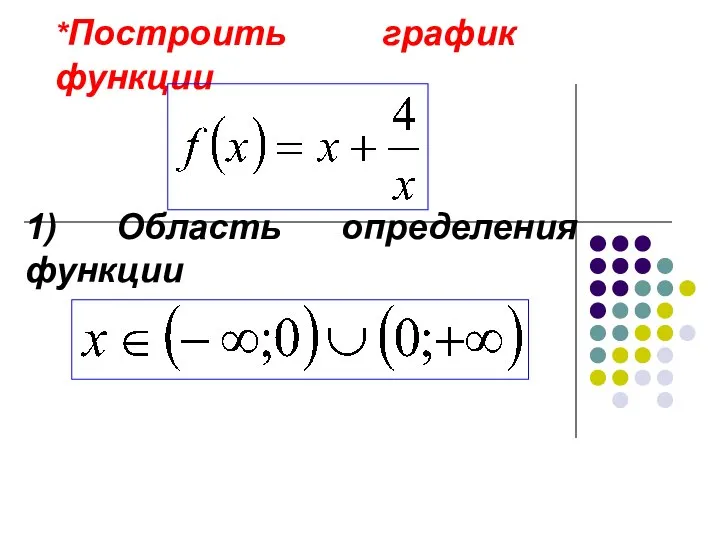 Построение графиков функций
Построение графиков функций Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ
Презентация на тему ОТЫСКАНИЕ ЧАСТИ ОТ ЦЕЛОГО И ЦЕЛОГО ПО ЕГО ЧАСТИ  Евклидовы пространства
Евклидовы пространства Среднее арифметическое. Размах. Мода
Среднее арифметическое. Размах. Мода Параллельность плоскостей
Параллельность плоскостей Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения
Обыкновенные дифференциальные уравнения первого порядка. Задача и теорема Коши. Общее и частное решения Метод составления уравнений неголономной механики в задаче волнового твердотельного гироскопа
Метод составления уравнений неголономной механики в задаче волнового твердотельного гироскопа Сложение десятичных дробей
Сложение десятичных дробей Рюкзак. Восстановление ответа
Рюкзак. Восстановление ответа Дискриминантный анализ Фишера с kernel trick
Дискриминантный анализ Фишера с kernel trick Степень числа
Степень числа Математическая викторина
Математическая викторина Геометрический конструктор GeoGebra
Геометрический конструктор GeoGebra Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений Как математика учит критическому мышлению
Как математика учит критическому мышлению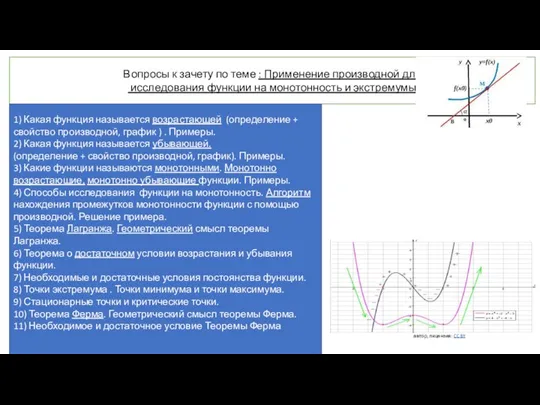 Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы Шарады, метаграммы, логогрифы
Шарады, метаграммы, логогрифы Определение высоты дерева
Определение высоты дерева 12. Тэтраэдр
12. Тэтраэдр Знакомимся с многоугольниками
Знакомимся с многоугольниками Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель: уч
Профессия математик - инновационные сферы применения знаний Исследователь: ученик 10 класса Романенко Николай Руководитель: уч Делениес остатком
Делениес остатком