Содержание
- 2. Цель: Рассмотрение основных свойств показательной функции. Построение графика. Решение показательных уравнений. Решение показательных неравенств.
- 3. Определение Показательная функция – это функция вида , где x – переменная, - заданное число, >0,
- 4. Свойства показательной функции Область определения: все действительные числа Множество значений: все положительные числа При > 1
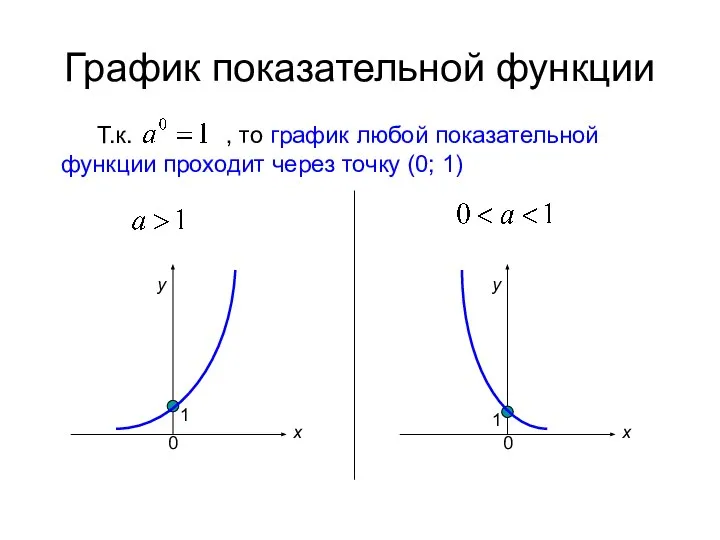
- 5. График показательной функции Т.к. , то график любой показательной функции проходит через точку (0; 1) 1
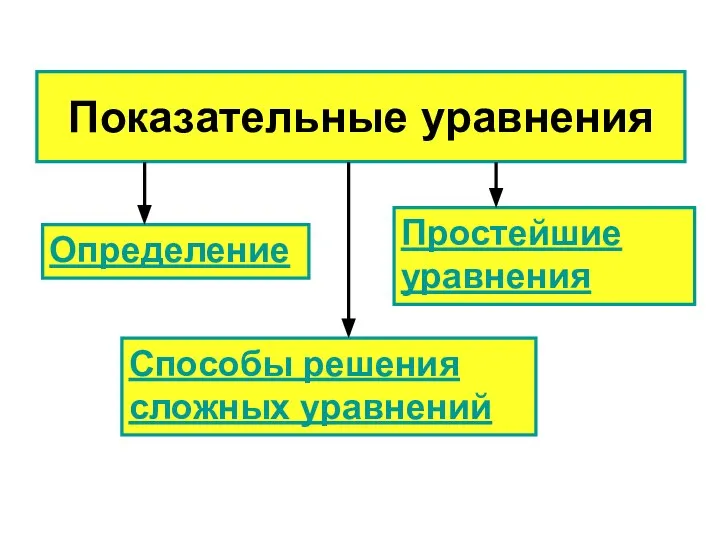
- 6. Показательные уравнения Определение Простейшие уравнения Способы решения сложных уравнений
- 7. Определение Уравнение, в котором переменная содержится в показателе степени, называется показательным. Примеры:
- 8. Простейшее показательное уравнение – это уравнение вида Простейшее показательное уравнение решается с использованием свойств степени.
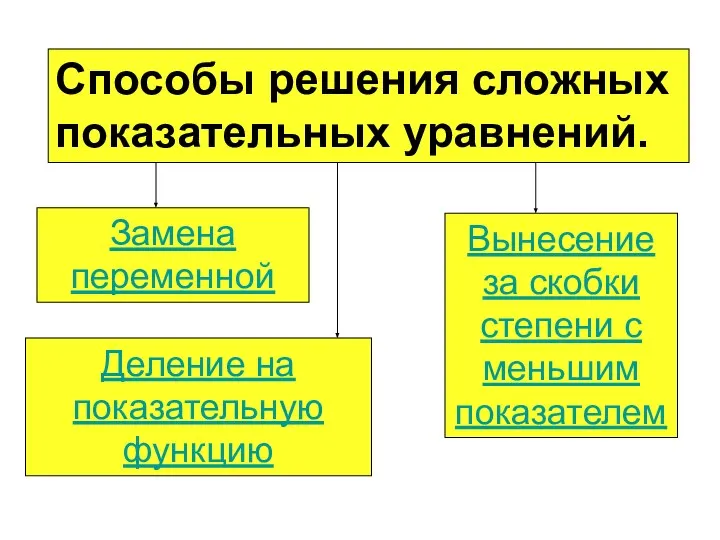
- 9. Способы решения сложных показательных уравнений. Вынесение за скобки степени с меньшим показателем Замена переменной Деление на
- 10. Вынесение за скобки степени с меньшим показателем Данный способ используется, если соблюдаются два условия: 1) основания
- 11. Замена переменной При данном способе показательное уравнение сводится к квадратному. Способ замены переменной используют, если показатель
- 12. Деление на показательную функцию Данный способ используется, если основания степеней разные. а) в уравнении вида ax
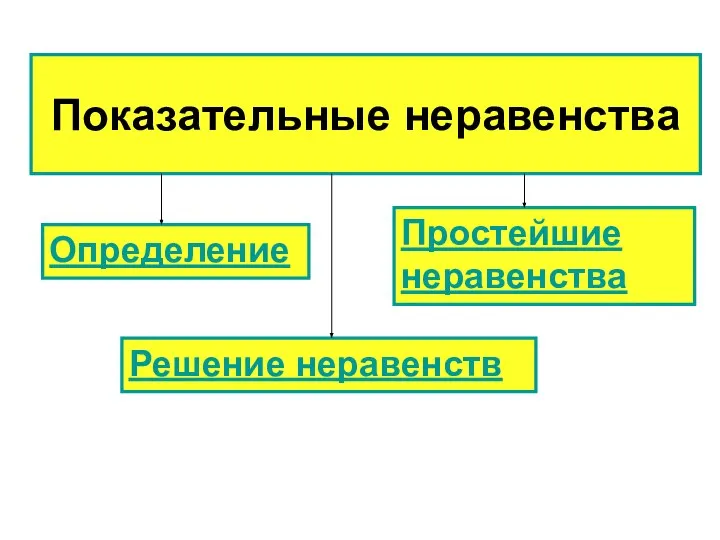
- 13. Показательные неравенства Определение Простейшие неравенства Решение неравенств
- 14. Определение Показательные неравенства – это неравенства, в которых неизвестное содержится в показателе степени. Примеры:
- 15. Простейшие показательные неравенства – это неравенства вида: где a > 0, a ≠ 1, b –
- 16. При решении простейших неравенств используют свойства возрастания или убывания показательной функции. Для решения более сложных показательных
- 17. Показательная функция Построение графика Сравнение чисел с использованием свойств показательной функции Сравнение числа с 1 а)
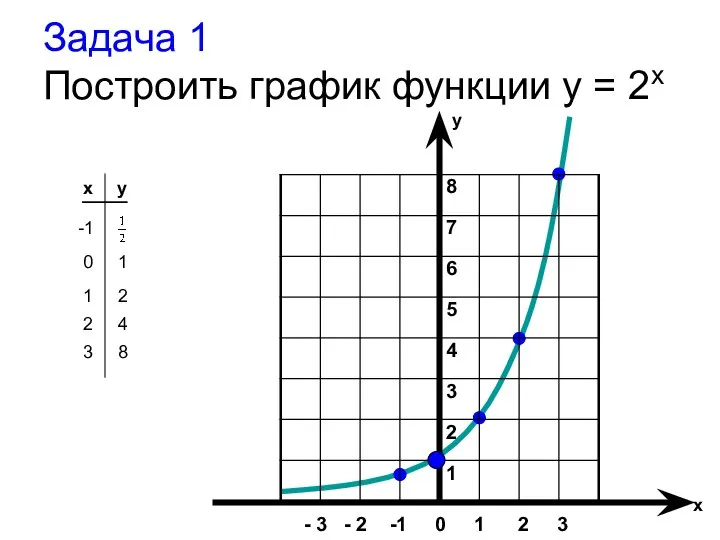
- 18. Задача 1 Построить график функции y = 2x x y -1 8 7 6 5 4
- 19. Задача 2 Сравнить числа Решение Ответ:
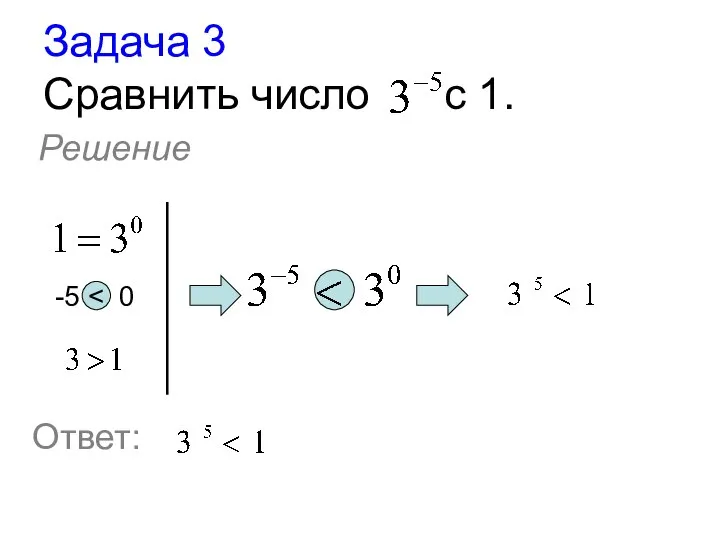
- 20. Задача 3 Сравнить число с 1. Решение -5 Ответ:
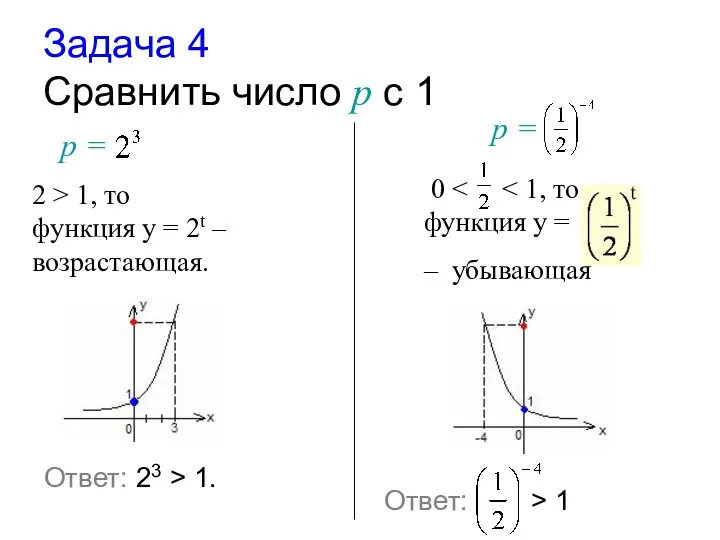
- 21. Задача 4 Cравнить число р с 1 р = 2 > 1, то функция у =
- 22. Решение показательных уравнений Простейшие показательные уравнения Уравнения, решаемые вынесением за скобки степени с меньшим показателем Уравнения,
- 23. Простейшие показательные уравнения Ответ: - 5,5. Ответ: 0; 3.
- 24. Вынесение за скобки степени с меньшим показателем Ответ: 5 x + 1 - (x - 2)
- 25. Замена переменной (1) основания степеней одинаковы, показатель одной из степеней в 2 раза больше, чем у
- 26. Замена переменной (2) Основания степеней одинаковы, коэффициенты перед переменной противоположны. По т. Виета: - Не удовлетворяет
- 27. Деление на показательную функцию Ответ: 0
- 28. Деление на показательную функцию Ответ: 0; 1.
- 29. Простейшие показательные неравенства Двойные неравенства Неравенства, решаемые вынесением за скобки степени с меньшим показателем Неравенства, решаемые
- 30. Простейшие показательные неравенства
- 31. Двойные неравенства Ответ: (- 4; -1). 3 > 1, то
- 32. Решение показательных неравенств Метод: Вынесение за скобки степени с меньшим показателем Ответ: х >3 Т.к. 3
- 33. Решение показательных неравенств Метод: Замена переменной Ответ: х 3>1, то
- 35. Скачать презентацию

























 Динамическое программирование
Динамическое программирование Классическое определение вероятности события
Классическое определение вероятности события Решение неравенств
Решение неравенств Система пропорционирования в проектировании объектов дизайна
Система пропорционирования в проектировании объектов дизайна Производная функции
Производная функции Создание системы внеклассной работы в физико-математическом образовании
Создание системы внеклассной работы в физико-математическом образовании Корень n-ой степени и его свойства
Корень n-ой степени и его свойства Представьте данные смешанные числа в виде неправильных дробей
Представьте данные смешанные числа в виде неправильных дробей Единицы площади
Единицы площади Определитель второго порядка
Определитель второго порядка Решение нелинейных уравнений
Решение нелинейных уравнений Решение логических задач
Решение логических задач Задачи на концентрацию, сплавы. Подготовка к ЕГЭ
Задачи на концентрацию, сплавы. Подготовка к ЕГЭ Параллельность прямых
Параллельность прямых Объем пирамиды
Объем пирамиды Издательство Легион. Задачи с параметром в ОГЭ
Издательство Легион. Задачи с параметром в ОГЭ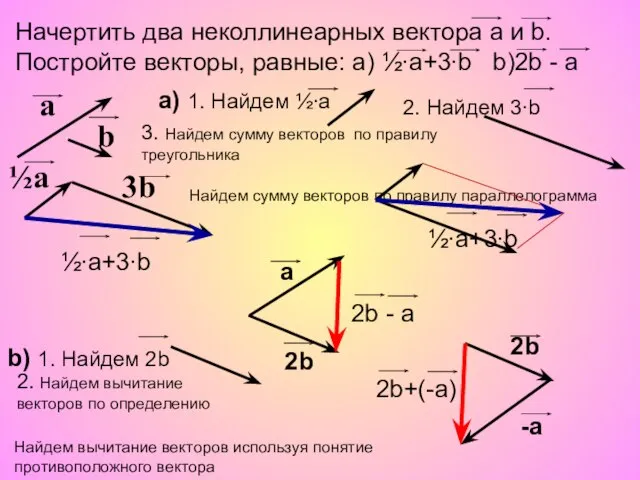 Векторы (9 класс) Задачи
Векторы (9 класс) Задачи Первообразная
Первообразная Способы задания зависимостей между величинами: аналитический, табличный, графический
Способы задания зависимостей между величинами: аналитический, табличный, графический Теорема Пифагора
Теорема Пифагора Занимательная геометрия
Занимательная геометрия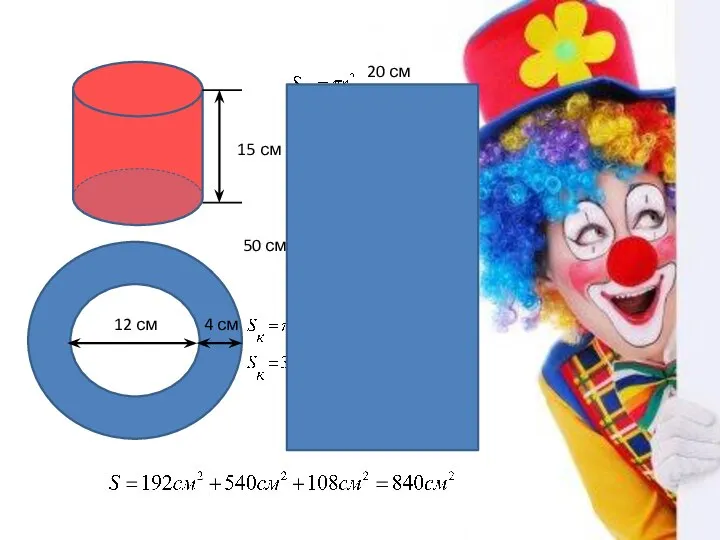 Площадь поверхности цилиндра
Площадь поверхности цилиндра Поверхностные интегралы первого рода
Поверхностные интегралы первого рода Определители. Обратная матрица. Ранг матрицы
Определители. Обратная матрица. Ранг матрицы Цилиндр. 11 класс
Цилиндр. 11 класс Цветочный город
Цветочный город Презентация на тему Величины (4 класс)
Презентация на тему Величины (4 класс)  Параллельность в пространстве
Параллельность в пространстве