Геометрия треугольника

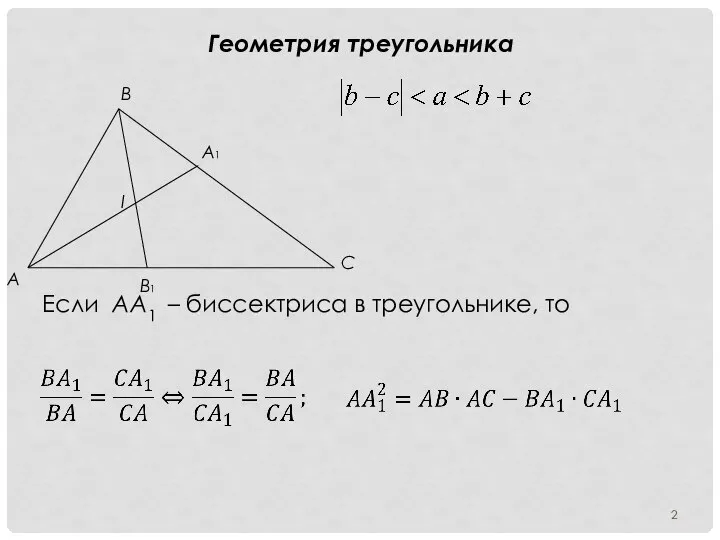
Геометрия треугольника
Если АА1 – биссектриса в треугольнике, то

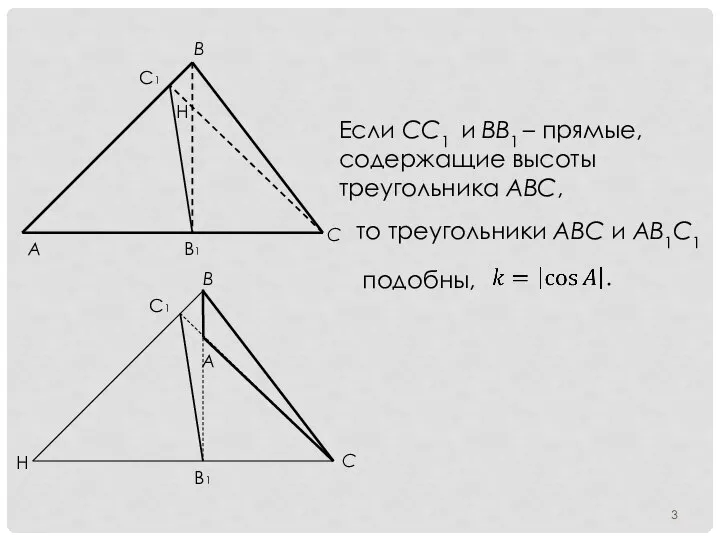
Если СС1 и ВВ1 – прямые, содержащие высоты треугольника АВС,
то треугольники АВС и АВ1С1
подобны,

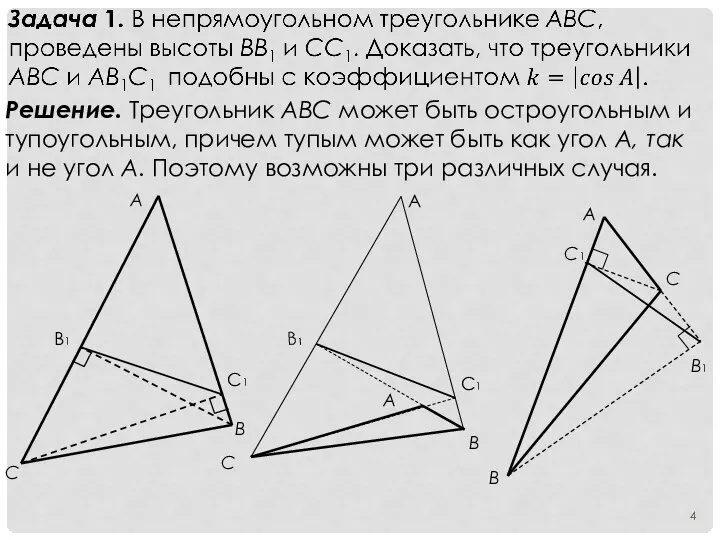
Решение. Треугольник АВС может быть остроугольным и тупоугольным, причем тупым может быть как угол А, так и не угол А. Поэтому возможны три различных случая.

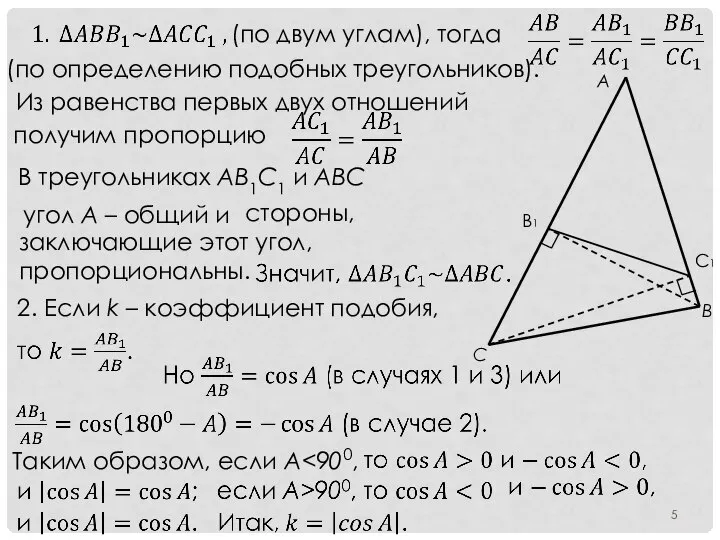
(по двум углам), тогда
(по определению подобных треугольников).
Из равенства первых двух отношений
В треугольниках AB1C1 и АВС
угол A – общий и
стороны,
2. Если k – коэффициент подобия,
Таким образом, если A<900,
получим пропорцию
заключающие этот угол, пропорциональны.

Комментарий к задаче
1. Приведенное выше решение не зависит от вида треугольника.
2. В доказательстве используется второй признак подобия треугольни­ков, что встречается довольно редко.
3. Задача может быть решена и другими средствами.
Так, наличие прямых углов наводит на мысль о дополнительном построении: здесь точки B, C, B1,C1 лежат на одной окружности,
Точки A,B1, C1 и точка
пересечения высот также лежат на одной окружности.
Приведенное выше решение представляется более экономным.
4. Из подобия треугольников AB1C1 и АВС можно вывести следствие о равенстве углов.

5. Если провести третью высоту – АА1,
то она пройдет через точку пересечения первых двух и эта точку мы называем ортоцентром, а треугольник А1B1C1 – называется ортоцентрическим.
Факт, доказанный в задаче 1, позволяет установить связь между углами (сторонами) исходного и ортоцентрического треугольников, что порождает довольно большую группу задач.

(формулы площадей треугольников, многоугольников, свойства площадей используются при решении задач и доказательстве теорем, в условиях и требованиях которых ничего не говорится о площадях.)
Метод площадей
Основные приемы
1. Линейные (угловые) элементы и соответствия между ними можно найти, применяя различные формулы для вычисления площади треугольника (многоугольника).
2. Если треугольник (многоугольник) разбит на несколько треугольников, то можно использовать свойство о том, что сумма площадей частей равна площади исходного многоугольника.
3. Отношение отрезков можно заменить отношением площадей треугольников

4. Если угол одного треугольника равен углу другого треугольника, то можно использовать тот факт, что отношение произведений сторон, заключающих равные углы, равно отношению площадей соответствующих треугольников
5. При доказательстве геометрических неравенств можно использовать неравенство для треугольника
Дополнительные построения в треугольнике
1. Строится биссектриса, медиана, высота к основанию в равнобедренном треугольнике.
2. Проводится высота к гипотенузе в прямоугольном треугольнике.

3. Удвоение медианы в треугольнике.
Появляются равные отрезки, равные углы, пары равных треугольников, параллелограмм
4. Если требуется получить половину отрезка, когда есть середина одной стороны треугольника, то может быть полезна средняя линия в треугольнике.
5. Если одна сторона в треугольнике в два раза больше другой, то проводится медиана к большей стороне.
6. Если один угол в треугольнике в два раза больше другого, то проводится биссектриса большего угла.
7. Если речь идет о сумме двух сторон, то на продолжении одной из них за общую вершину откладывают другую.
Если речь идет о разности сторон, то от их общей вершины на большей стороне откладывается меньшая.

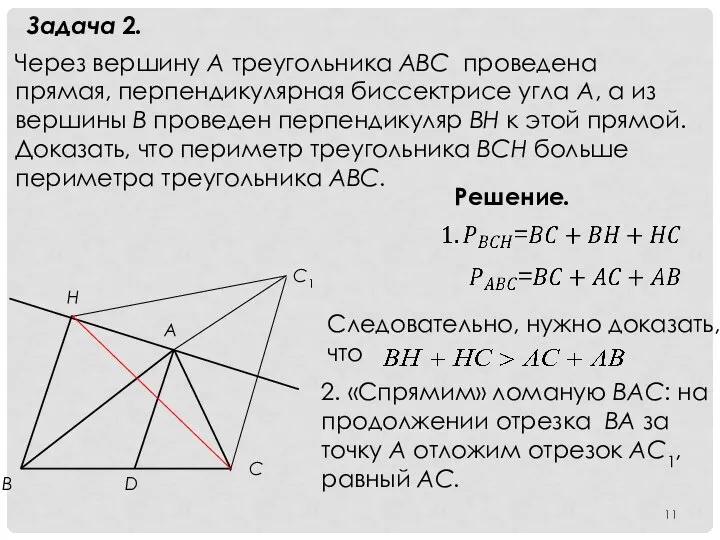
Задача 2.
Через вершину А треугольника АВС проведена прямая, перпендикулярная биссектрисе угла А, а из вершины В проведен перпендикуляр ВН к этой прямой. Доказать, что периметр треугольника ВСН больше периметра треугольника АВС.
Следовательно, нужно доказать,
что
.
2. «Спрямим» ломаную ВАС: на продолжении отрезка ВА за точку А отложим отрезок АС1, равный АС.
Решение.

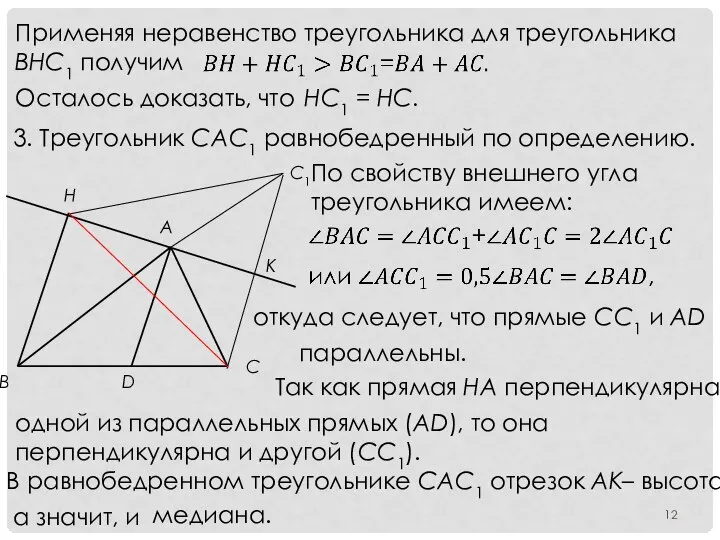
Применяя неравенство треугольника для треугольника ВНС1 получим
Осталось доказать, что
HC1 = HC.
3. Треугольник САС1 равнобедренный по определению.
По свойству внешнего угла треугольника имеем:
откуда следует, что прямые CC1 и AD
параллельны.
Так как прямая НА перпендикулярна
одной из параллельных прямых (AD), то она перпендикулярна и другой (CC1).
В равнобедренном треугольнике CAC1 отрезок AK
– высота,
а значит, и
медиана.
К

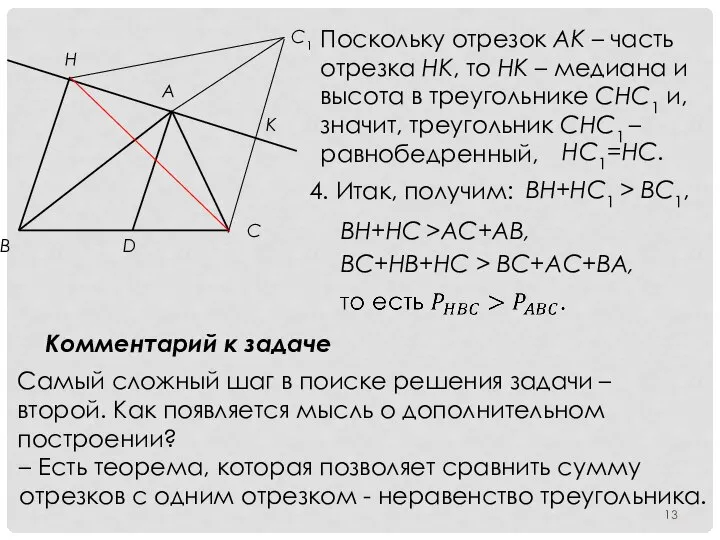
Поскольку отрезок AK – часть отрезка HK, то HK – медиана и высота в треугольнике CHC1 и,
значит, треугольник CHC1 – равнобедренный,
HC1=HC.
4. Итак, получим:
BH+HC1 > BC1,
BH+HC >AC+AB,
BC+HB+HC > BC+AC+BA,
Комментарий к задаче
Самый сложный шаг в поиске решения задачи – второй. Как появляется мысль о дополнительном построении?
– Есть теорема, которая позволяет сравнить сумму отрезков с одним отрезком - неравенство треугольника.
K

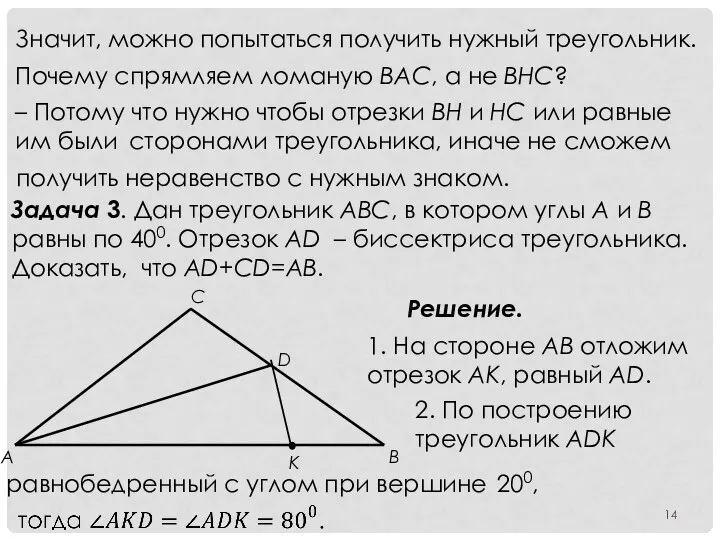
Значит, можно попытаться получить нужный треугольник.
Почему спрямляем ломаную BAC, а не BHC?
– Потому что нужно чтобы отрезки BH и HC или равные им были
сторонами треугольника, иначе не сможем
получить неравенство с нужным знаком.
Задача 3. Дан треугольник АВС, в котором углы А и В равны по 400. Отрезок AD – биссектриса треугольника. Доказать, что AD+CD=AB.
Решение.
1. На стороне AB отложим отрезок AK, равный AD.
2. По построению треугольник ADK
равнобедренный с углом при вершине
200,

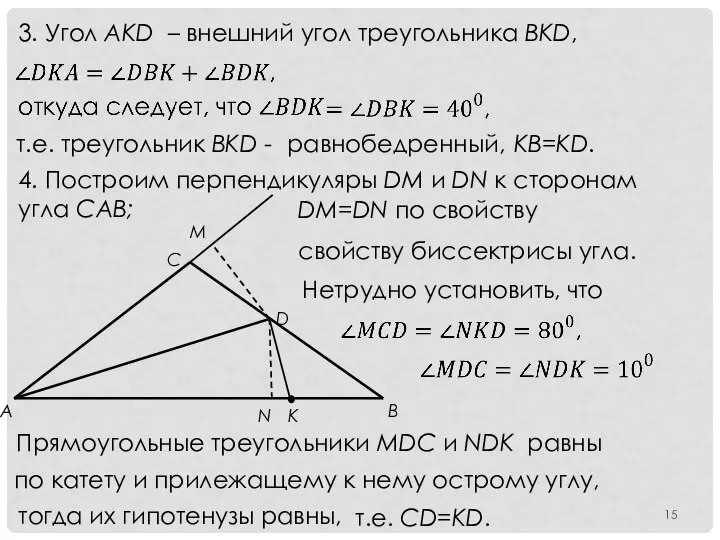
3. Угол AKD – внешний угол треугольника BKD,
т.е. треугольник BKD -
равнобедренный,
KB=KD.
4. Построим перпендикуляры DM и DN к сторонам угла CAB;
DM=DN по свойству
свойству биссектрисы угла.
Нетрудно установить, что
Прямоугольные треугольники MDC и NDK равны
по катету и прилежащему к нему острому углу,
тогда их гипотенузы равны,
т.е. CD=KD.

5. Из равенств KB=KD и CD=KD получим, что
KB=CD.
Итак, AD+CD=AK+KB=AB.
Комментарий к задаче
1. Как и в первой задаче, здесь потребовалось дополнительное построение. Однако, несмотря на то, что в обоих случаях задействована сумма отрезков, дополнительные построения выполняются разные.
Выведем такую эвристику: если требуется доказать, что сумма двух данных отрезков равна третьему, тоже известному отрезку, то можно от конца отрезка -результата на нем отложить отрезок, равный одному из слагаемых, и доказать, что отрезок-остаток равен второму слагаемому.
Поскольку равенства a - b =c и a = c + b равносильны,
то аналогичным образом можно поступать, если требуется доказать, что разность двух отрезков равна третьему.

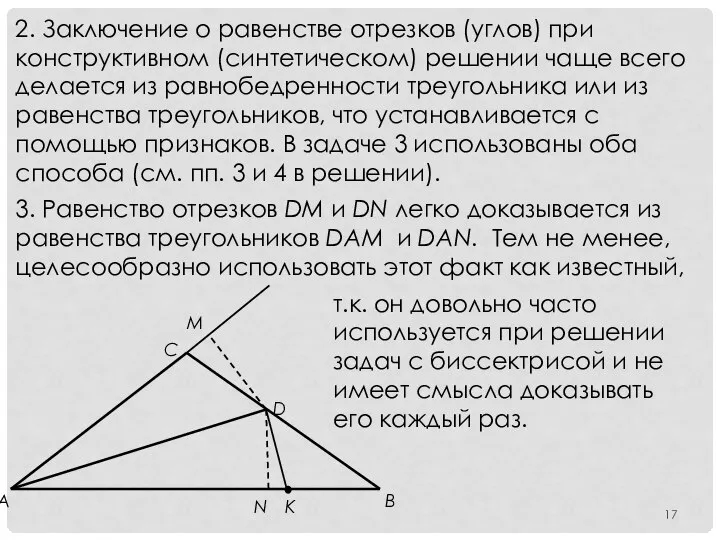
2. Заключение о равенстве отрезков (углов) при конструктивном (синтетическом) решении чаще всего делается из равнобедренности треугольника или из равенства треугольников, что устанавливается с помощью признаков. В задаче 3 использованы оба способа (см. пп. 3 и 4 в решении).
3. Равенство отрезков DM и DN легко доказывается из равенства треугольников DAM и DAN. Тем не менее, целесообразно использовать этот факт как известный,
т.к. он довольно часто используется при решении задач с биссектрисой и не имеет смысла доказывать его каждый раз.

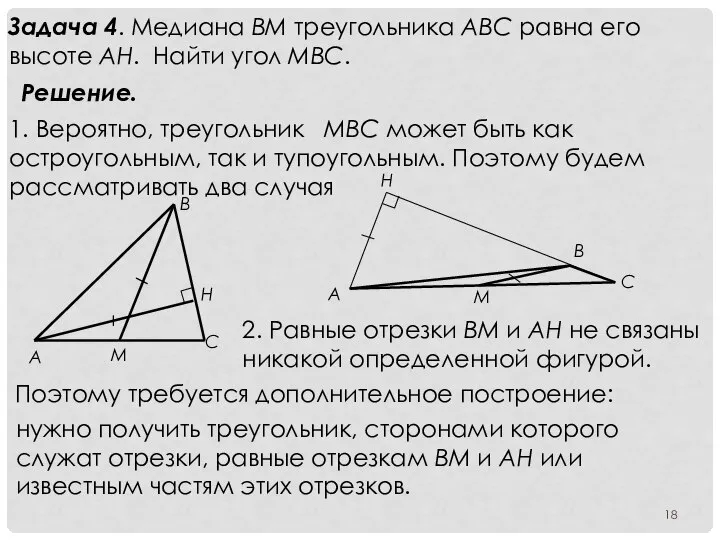
Задача 4. Медиана ВМ треугольника АВС равна его высоте АН. Найти угол МВС.
Решение.
1. Вероятно, треугольник МВС может быть как остроуголь­ным, так и тупоугольным. Поэтому будем рассматривать два случая
По­этому требуется дополнительное построение:
нужно получить треугольник, сторонами которого служат отрезки, равные отрезкам ВМ и АН или известным частям этих отрезков.
2. Равные отрезки ВМ и АН не связаны никакой определенной фигурой.

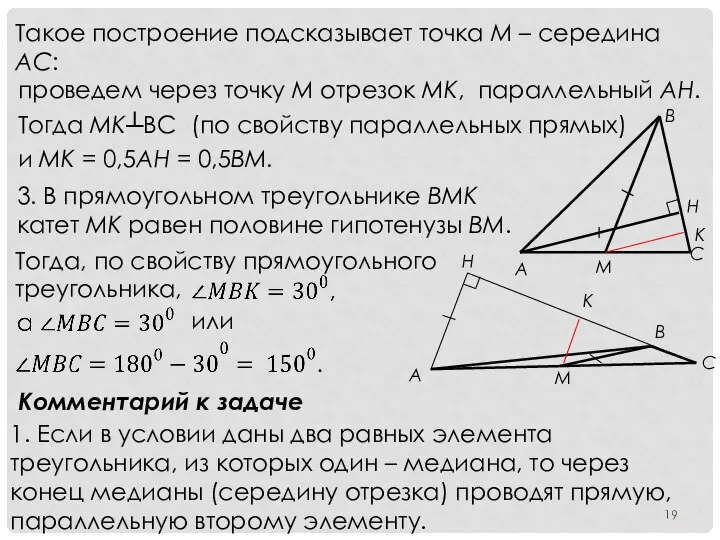
Такое построение подсказывает точка М – середина АС:
проведем через точку М отрезок МК, параллельный АН.
Тогда МК┴ВС
(по свойству параллельных прямых)
и МК = 0,5АН = 0,5ВМ.
3. В прямоугольном треугольнике ВМК катет МК равен половине гипотенузы ВМ.
Тогда, по свойству прямоугольного треугольника,
или
Комментарий к задаче
1. Если в условии даны два равных элемента треугольника, из которых один – медиана, то через конец медианы (середину отрезка) проводят прямую, параллельную второму элементу.

Здесь можно было выполнить другое стандартное дополнительное построение – удвоение медианы. Получили бы параллелограмм, например, ABCD.
Затем через точку D нужно было бы провести DN параллельноAH,
Этот способ решения был бы несколько длиннее.
2. Если в треугольнике задано отношение равенства двух отрезков и требуется найти угол, то нередко случается, что он оказывается элементом треугольника особого вида: равностороннего, прямоугольного равнобедренного или прямоугольного, в котором катет в два раза меньше гипотенузы.

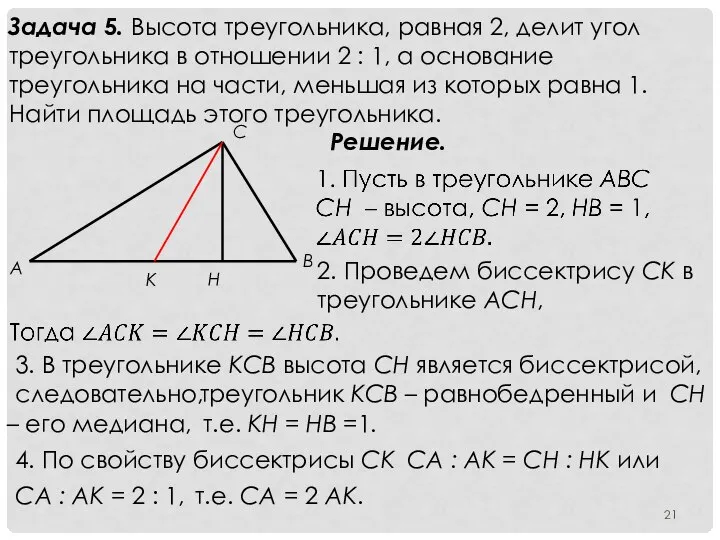
Задача 5. Высота треугольника, равная 2, делит угол треугольника в отношении 2 : 1, а основание треугольника на части, меньшая из которых равна 1. Найти площадь этого треугольника.
Решение.
2. Проведем биссектрису CK в треугольнике ACH,
3. В треугольнике KCB высота CH является биссектрисой, следовательно,
треугольник KCB – равнобедренный и CH
– его медиана,
т.е. KH = HB =1.
4. По свойству биссектрисы CK
CA : AK = CH : HK или
CA : AK = 2 : 1,
т.е. CA = 2 AK.

5. Для сокращения записей введем обозначение: AK = x, AC = 2x.
В прямоугольном треугольнике ACH имеем:
AC = 2x, AH = x+1, CH = 2.
Применяя к нему теорему Пифагора, получим уравнение
Уравнение имеет корни -1 и 5/3.
Следовательно, AK = 5/3, AB = AK+ AB = 11/3.
Комментарий к задаче
1. Задачи 1-4 решены конструктивным (или его называют синтетическим) методом. Задача 5 - алгебраическим методом. В ней при­шлось решать квадратное уравнение. В других задачах могут быть

использо­ваны и линейные уравнения, и уравнения более высоких степеней, системы уравнений, неравенства.
2. Наличие условия о том, что один из углов в 2 раза больше другого, наводит на мысль о проведении
биссектрисы большего угла.
оказалась плодотворной: получили биссектрисы в двух треугольниках и использовали разные их свойства, которые дали результат.
В данном случае мысль
3. Теорема Пифагора используется не только для нахождения длины от­резка, но и для получения уравнения с неизвестными.

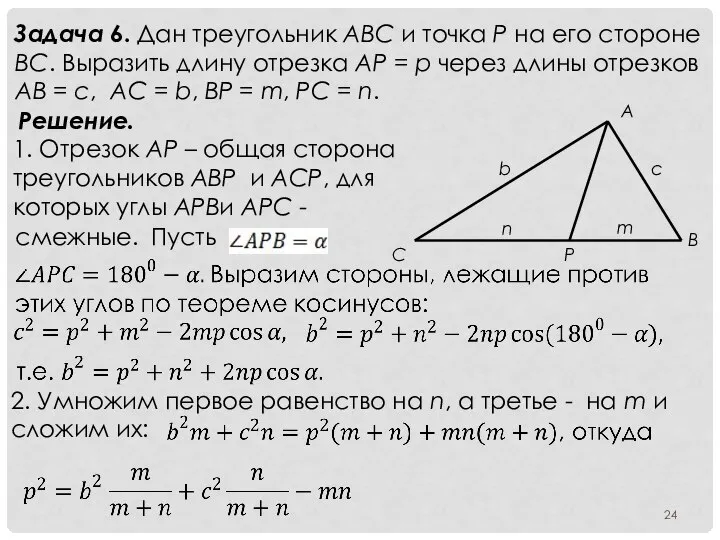
Задача 6. Дан треугольник ABC и точка P на его стороне BC. Выразить длину отрезка AP = p через длины отрезков AB = c, AC = b, BP = m, PC = n.
Решение.
1. Отрезок AP – общая сторона треугольников ABP и ACP, для которых углы APBи APC -
смежные.
Пусть
2. Умножим первое равенство на n, а третье - на m и сложим их:
b
c
m
n

Комментарий к задаче
1. Для нахождения зависимости между длинами отрезков может быть ис­пользована теорема косинусов. При этом довольно часто она записывается не для искомого отрезка, а для известного
2. Полученный в задаче факт впервые установил английский математик М.Стюарт и опубликовал его в труде «Некоторые общие теоремы» в 1746 году. Соответствующая теорема носит имя Стюарта.
3. Если AP – медиана в треугольнике ABC, то n = m = 0,5a. Если AP - биссектриса, то с : b = m : n и
и
Исполь­зуя теорему Стюарта, или проводя рассуждения, как и в задаче 6, по­лучим:
и

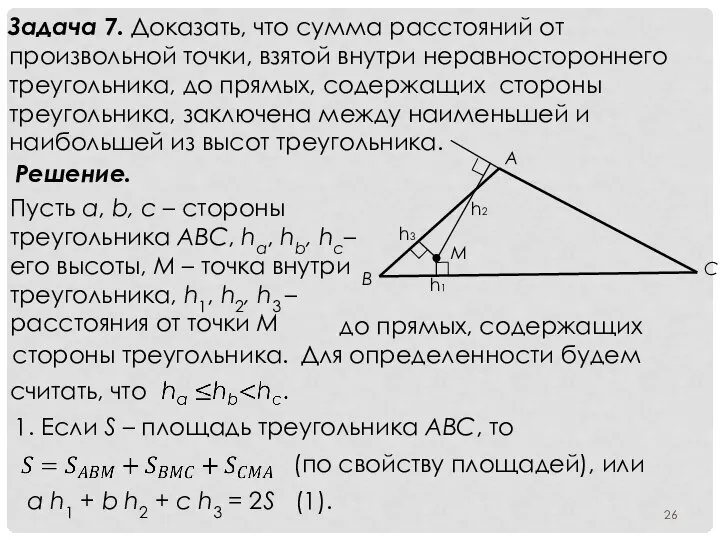
Задача 7. Доказать, что сумма расстояний от произвольной точки, взя­той внутри неравностороннего треугольника, до прямых, содержащих сто­роны треугольника, заключена между наименьшей и наибольшей из высот треугольника.
Решение.
Пусть a, b, c – стороны треугольника ABC, ha, hb, hc– его высоты, M – точка внутри треугольника, h1, h2, h3 – расстояния от точки M
стороны треугольника.
до прямых, содержащих
Для определенности будем
считать, что
1. Если S – площадь треугольника ABC, то
(по свойству площадей), или
a h1 + b h2 + c h3 = 2S (1).

Из формул для площади
треугольника находим
Подставляя в равенство (1) вместо a, b, c их выражения через площадь и упрощая, получим
2. Умножим обе части равенства (2) на ha
Так как ha – наименьшая из высот или ha = hb, то
Учитывая последние два неравенства, из равенства (3) получим:
Аналогично докажем, что