Содержание
- 2. Математика - наиболее совершенный способ водить самого себя за нос. А. ЭЙНШТЕЙН
- 3. 1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
- 4. 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ Матрицей размера m x n называется прямоугольная таблица чисел, содержащая
- 5. Обозначение: Где i=1,2…m j=1,2…n - матрица размерности m x n - элемент матрицы i –ой строки
- 6. матрица размерности m x n 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 7. Две матрицы называются равными, если у них одинаковая размерность и совпадают строки и столбцы. Если число
- 8. Пример: - квадратная матрица размерности 3х3 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 9. Элементы матрицы aij , у которых номер столбца совпадает с номером строки, называются диагональными. Если в
- 10. единичная матрица 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 11. Матрица любого размера называется нулевой, если все ее элементы равны 0. нулевая матрица 1.1. МАТРИЦЫ И
- 12. Матрица, состоящая из одной строки, называется матрицей-строкой или вектором-строкой. матрица-строка 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 13. Матрица, состоящая из одного столбца, называется матрицей-столбцом или вектором-столбцом. матрица-столбец 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
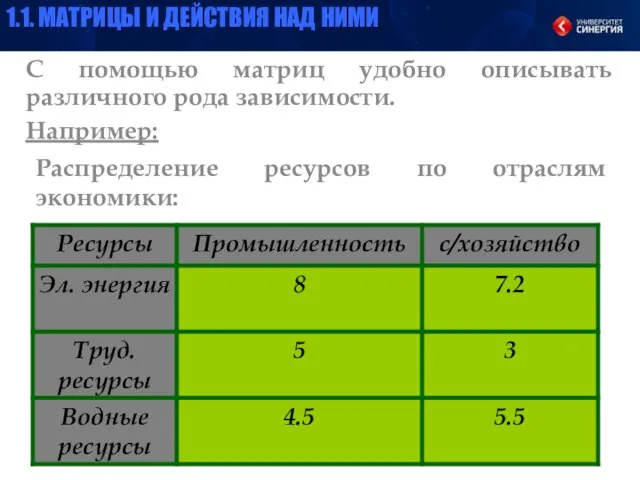
- 14. Распределение ресурсов по отраслям экономики: С помощью матриц удобно описывать различного рода зависимости. Например: 1.1. МАТРИЦЫ
- 15. Эту зависимость можно представить в виде матрицы: Где элемент aij показывает сколько i – го ресурса
- 16. ДЕЙСТВИЯ НАД МАТРИЦАМИ 1. Умножение матрицы на число Чтобы умножить матрицу на число, надо каждый элемент
- 17. Пусть дана матрица Умножаем ее на число λ: Где каждый элемент матрицы В: Где: 1.1. МАТРИЦЫ
- 18. Например: Умножая матрицу на число 2, получим: 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 19. 2. Сложение матриц Складываются матрицы одинаковой размерности. Получается матрица той же размерности, каждый элемент которой равен
- 20. Пусть даны матрицы Складываем их: Где каждый элемент матрицы С: Аналогично проводится вычитание матриц. 1.1. МАТРИЦЫ
- 21. Пример. Найти сумму и разность матриц: 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 22. Решение: 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 23. 3. Умножение матриц Умножение матриц возможно, если число столбцов первой матрицы равно числу строк второй. Тогда
- 24. Пусть даны матрицы Умножаем их: Где каждый элемент матрицы С: 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 25. Пример. Найти произведение матриц: 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 26. Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует: Решение: 1.1. МАТРИЦЫ И
- 27. Теперь перемножим матрицы в обратном порядке: Умножение матриц в общем случае некоммутативно: 1.1. МАТРИЦЫ И ДЕЙСТВИЯ
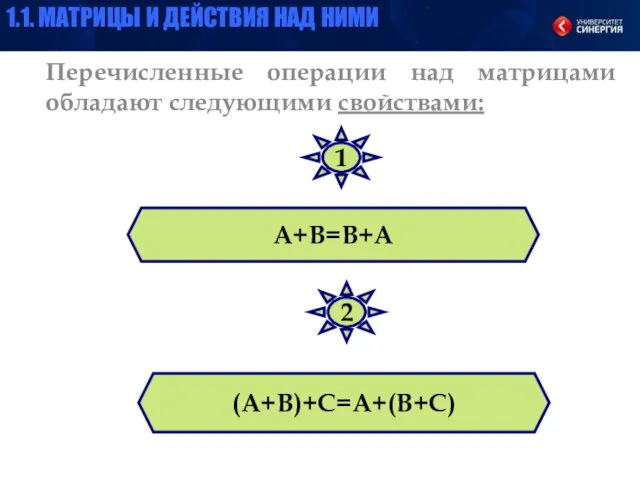
- 28. Перечисленные операции над матрицами обладают следующими свойствами: А+В=В+А (А+В)+С=А+(В+С) 1 2 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД
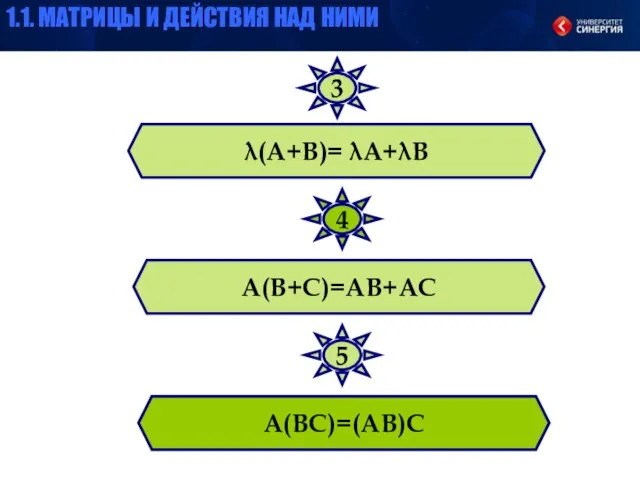
- 29. λ(А+В)= λА+λВ А(В+С)=АВ+АС А(ВС)=(АВ)С 3 4 5 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 30. 4. Транспонирование матриц Матрица АТ называется транспонированной к матрице А, если в ней поменяли местами строки
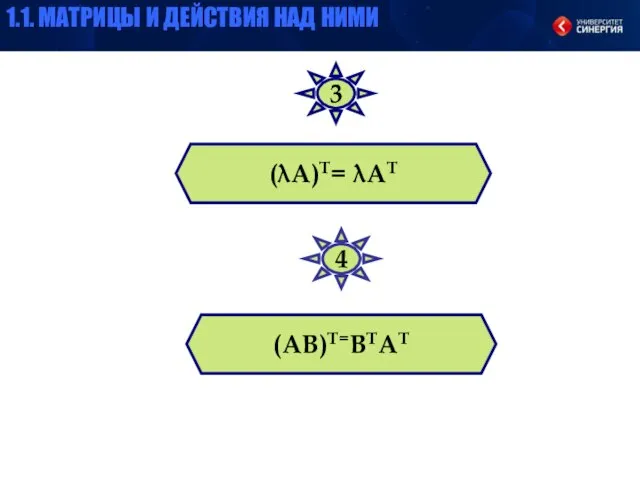
- 31. (АТ)Т=А (А+В)Т=АТ+ВТ свойства операции траспонирования: 1 2 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 32. (λА)Т= λАТ (АВ)Т=ВТАТ 3 4 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 33. Пример. Транспонировать матрицу: 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 34. Решение: 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 35. 1.1. МАТРИЦЫ И ДЕЙСТВИЯ НАД НИМИ
- 37. Скачать презентацию






























 Одночлен и его стандартный вид
Одночлен и его стандартный вид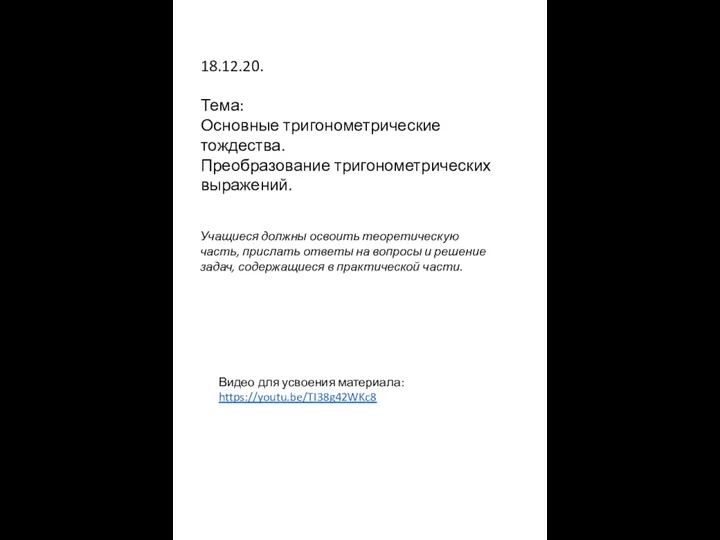 Тригонометрические тождества. Преобразование тригонометрических выражений
Тригонометрические тождества. Преобразование тригонометрических выражений комбинаторика 1 лекция-1
комбинаторика 1 лекция-1 Определение и знаки тригонометрических функций
Определение и знаки тригонометрических функций Топология
Топология Штангенциркуль
Штангенциркуль Занимательная математика (3 класс)
Занимательная математика (3 класс) Запись Арифметических выражений и на языке программирования Паскаль
Запись Арифметических выражений и на языке программирования Паскаль Одночлены
Одночлены Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана
Числовые характеристики дискретной случайной величины (ДСВ). Математическое ожидание, мода, медиана Построение графиков тригонометрических функций
Построение графиков тригонометрических функций Презентация на тему Треугольники (5 класс)
Презентация на тему Треугольники (5 класс)  Усный счет
Усный счет Перпендикуляр и наклонная. 8 класс
Перпендикуляр и наклонная. 8 класс Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Завдання на відсотки
Завдання на відсотки Сравнение десятичных дробей
Сравнение десятичных дробей Формулы сокращённого умножения
Формулы сокращённого умножения Арифметическая и геометрическая прогрессии
Арифметическая и геометрическая прогрессии Свойства точек числовой окружности
Свойства точек числовой окружности Решение задач с помощью систем уравнений (часть 2)
Решение задач с помощью систем уравнений (часть 2) Модуль числа. 6 класс
Модуль числа. 6 класс Деление десятичной дроби на натуральное число. Графический диктант
Деление десятичной дроби на натуральное число. Графический диктант Osnovnoe_svoystvo_drobi (1)
Osnovnoe_svoystvo_drobi (1) Презентация на тему Математика в профессиях (11 класс)
Презентация на тему Математика в профессиях (11 класс)  Явная разностная схема для полной системы уравнений Навье-Стокса
Явная разностная схема для полной системы уравнений Навье-Стокса Урок математики в 1 классе
Урок математики в 1 классе Статистическое изучение связей между явлениями (4 часа). Тема 1.7
Статистическое изучение связей между явлениями (4 часа). Тема 1.7