Содержание
- 2. Прямоугольная система координат Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них
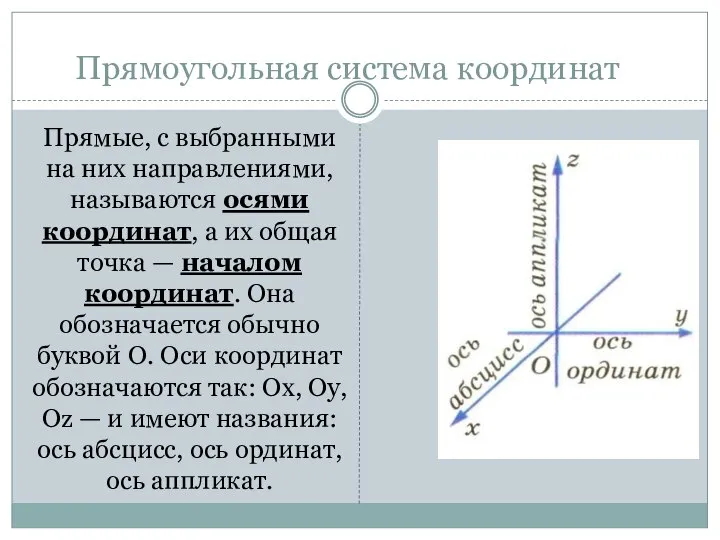
- 3. Прямые, с выбранными на них направлениями, называются осями координат, а их общая точка — началом координат.
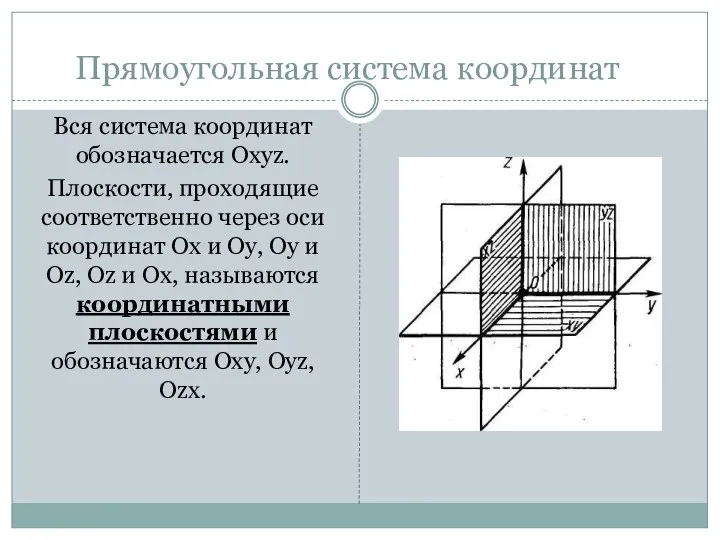
- 4. Прямоугольная система координат Вся система координат обозначается Охуz. Плоскости, проходящие соответственно через оси координат Ох и
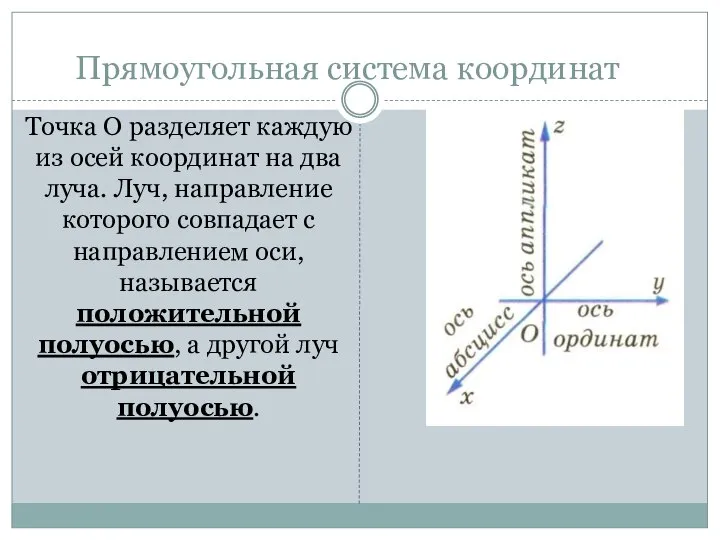
- 5. Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением
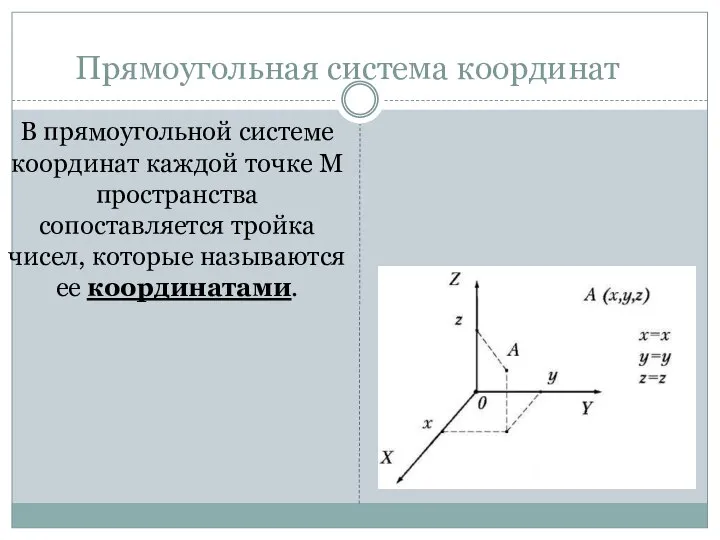
- 6. В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел, которые называются ее координатами. Прямоугольная
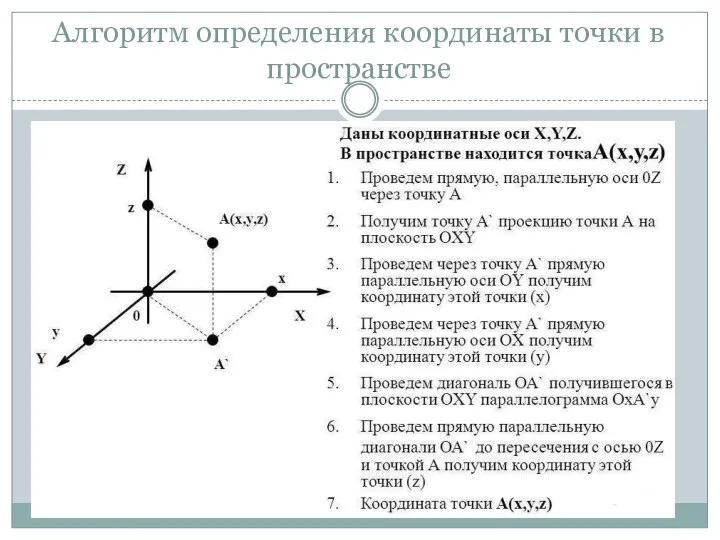
- 7. Алгоритм определения координаты точки в пространстве
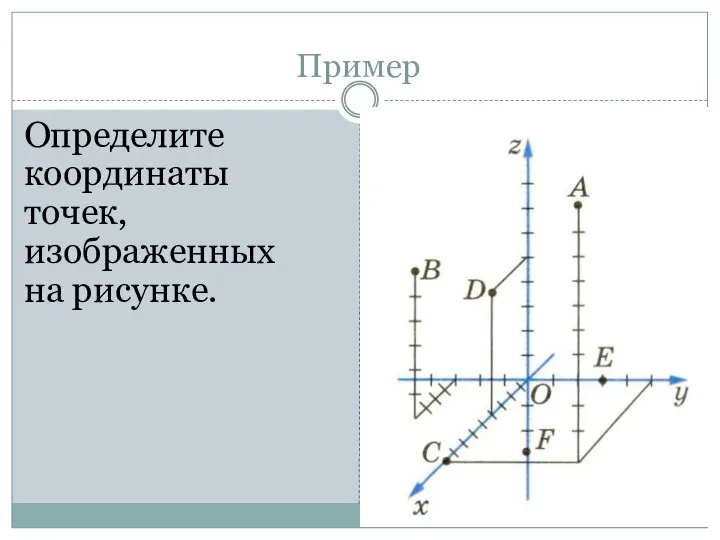
- 8. Определите координаты точек, изображенных на рисунке. Пример
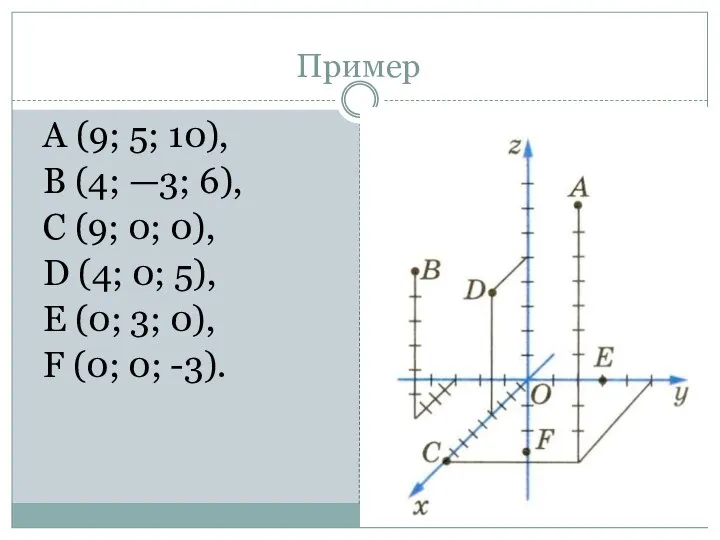
- 9. А (9; 5; 10), В (4; —3; 6), С (9; 0; 0), D (4; 0; 5),
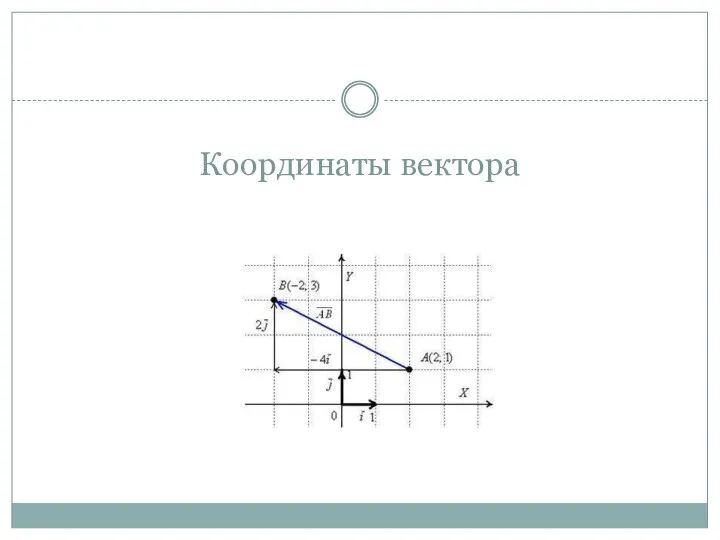
- 10. Координаты вектора
- 11. Что такое вектор? Вектором называется направленный отрезок, для которого указано его начало и конец. В данном
- 12. Любой вектор можно разложить по координатным векторам, т. е. представить в виде причем коэффициенты разложения х,
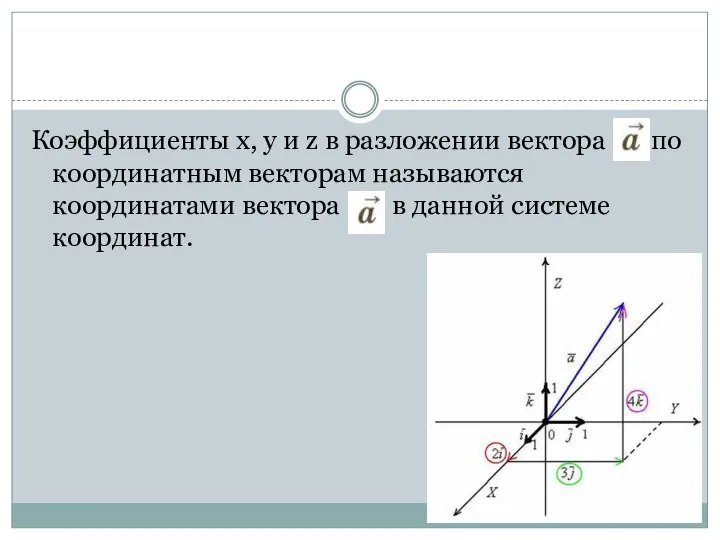
- 13. Коэффициенты х, у и z в разложении вектора по координатным векторам называются координатами вектора в данной
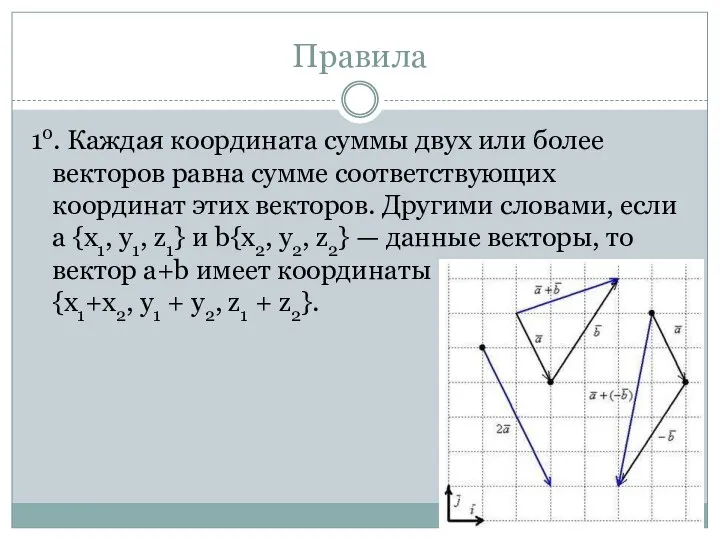
- 14. Правила 10. Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими
- 15. Правила 20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Другими словами, если
- 16. Правила 30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
- 18. Скачать презентацию





 Момент силы относительно точки О
Момент силы относительно точки О Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»
Координатный метод в решении задач на плоскости Белобородова Н. Е., учитель математики МАОУ «СОШ №2»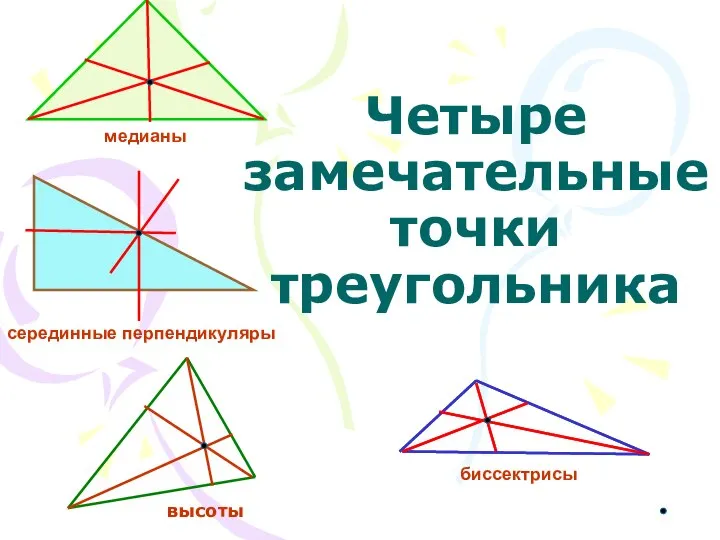 Четыре замечательные точки треугольника
Четыре замечательные точки треугольника Производная суммы, произведения и частного двух функций
Производная суммы, произведения и частного двух функций Задачи на построение сечений. 10 класс
Задачи на построение сечений. 10 класс Площадь ромба
Площадь ромба Проценты. Задачи на концентрацию, сплавы. ЕГЭ В11
Проценты. Задачи на концентрацию, сплавы. ЕГЭ В11 Расширение и углубление знаний учащихся о преобразованиях графиков функций
Расширение и углубление знаний учащихся о преобразованиях графиков функций 2._3
2._3 Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը
Խնդիր Հաշվել a, b, c կողմեր ունեցող եռանկյան մակերեսը Основные тригонометрические тождества. Формулы приведения
Основные тригонометрические тождества. Формулы приведения Решение уравнений. Буквенные выражения
Решение уравнений. Буквенные выражения Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной
Выделение целой части из неправильной дроби и представление смешанной дроби в виде неправильной Взаимное расположение прямой и окружности (7 класс)
Взаимное расположение прямой и окружности (7 класс) Геометрия и искусство
Геометрия и искусство Формулы двойного аргумента
Формулы двойного аргумента Вариационно-статистический метод анализа
Вариационно-статистический метод анализа Занимательная математика.Игры с кубиками, 1 класс
Занимательная математика.Игры с кубиками, 1 класс Таблица умножения на 2
Таблица умножения на 2 Цифра 10
Цифра 10 Координатная плоскость
Координатная плоскость Презентация на тему Евклид
Презентация на тему Евклид  Задания для домашнего обучения
Задания для домашнего обучения Понятие теории игр
Понятие теории игр Иррациональные уравнения (часть 1)
Иррациональные уравнения (часть 1) Углы треугольника
Углы треугольника Математическое моделирование. Линейное программирование
Математическое моделирование. Линейное программирование Рівнобедрений трикутник і його властивості
Рівнобедрений трикутник і його властивості