Статистические оценки параметров распределения. Точечные и интервальные оценки

При изучении случайной величины X, распределенной в генеральной совокупности, часто из теоретических соображений удается установить вид распределения и по данным выборки необходимо оценить (приближенно найти) его численные параметры.
Например, если случайная величина имеет нормальное распределение, то для полного его определения необходимо оценить его математическое ожидание и среднее квадратическое отклонение.

оценки параметров распределения
Точечная оценка неизвестного параметра
Интервальная оценка неизвестного параметра

Несмещенные, состоятельные и эффективные оценки
Для того, чтобы статистической оценке можно было доверять, она должна обладать некоторыми свойствами.
Точечные оценки

Оценки

Несмещенные, состоятельные и эффективные оценки
З. На практике не всегда удается добиться выполнения всех трех требований к оценке. Соображения практической удобности заставляют пользоваться не полностью адекватными оценками, но необходимо представлять, каким свойством мы пренебрегаем. Ниже, при рассмотрении конкретных оценок, эти аспекты будут обсуждаться.

Точечная оценка генерального среднего по выборочному среднему

Точечная оценка генерального среднего по выборочному среднему

Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии
Можно показать, что выборочная дисперсия (среднее значение квадрата отклонения) является смещенной оценкой генеральной дисперсии.

Точечная оценка генеральной дисперсии по исправленной выборочной дисперсии
Для получения несмещенной оценки достаточно перейти к исправленной выборочной дисперсии

Интервальные оценки

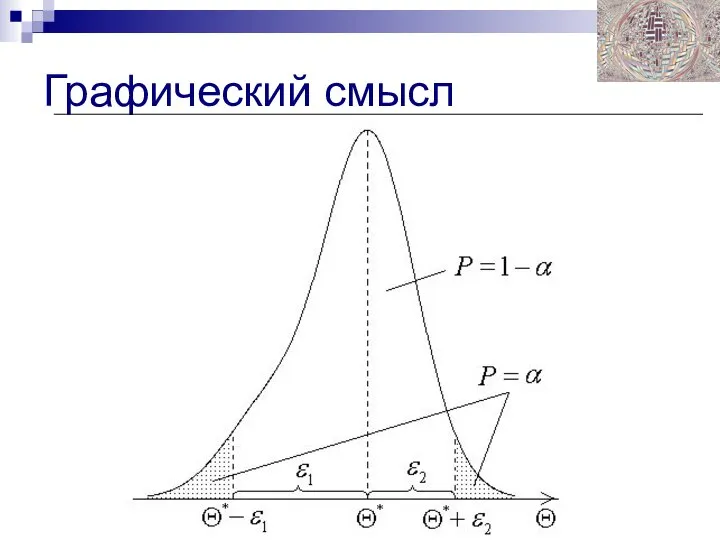
Графический смысл

Интервальные оценки

Точечные оценки проще в вычислении, но не позволяют установить степень достоверности оценки.
Интегральные оценки, наряду с возможными границами значений параметра, дают вероятность, с которой истинное значение параметра лежит между этими (случайными) границами.
Естественно, чем больше надежность оценки, тем шире доверительный интервал, и наоборот, так что практические вычисления являются компромиссом между точностью и надежностью оценки. Наиболее часто задают надежность 0,95; 0,99 и 0,999.

Интервальные оценки

для получения интервальной оценки
Как правило вид генерального распределения постулируется(нормальное распределение, равномерное распределение и т.д.). При достаточно большом объеме выборки реальную функцию распределения оценки с достаточной точностью можно заменить асимптотической
Значения параметров генерального распределения оценивают либо приближенно либо точно.

Приближенный способ
состоит в замене неизвестных параметров генеральной совокупности, от которых зависит распределение , на их точечные оценки, полученные в результате выборки.
Далее оценка строится, как если бы параметры распределения были бы известны.

Точный способ
может быть использован лишь в том случае, когда известен закон генерального распределения. При этом строятся вспомогательные случайные величины, распределение которых зависит лишь от объема выборки.
В частности, при оценке среднего значения нормально распределенной генеральной совокупности можно использовать оценку
которая подчиняется распределению Стьюдента, зависящему только от объема выборки .

С интервальной оценкой связано решение трех типов задач
1) определение доверительной вероятности по заданному доверительному интервалу и объему выборки;
2) определение доверительного интервала по заданной доверительной вероятности и объему выборки;
3) определение необходимого объема выборки по заданным доверительной вероятности и доверительному интервалу

Интервальная оценка математического ожидания нормально распределенной случайной величины при известном σ

Интервальная оценка математического ожидания нормально распределенной случайной величины при известном σ

1) Определим, с какой надежностью математическое ожидание а покрывается доверительным интервалом при заданной точности ε, т.е. найдем

2) По выборочному значению математического
ожидания и известному σ найти доверительный интервал, который с заданной надежностью γ покрывает математическое ожидание а генеральной совокупности. Это и есть задача получения интервальной оценки

3) По заданным σ, ε и γ, используя соотношение , найти объем выборки n.

Пример:
1:

Пример:
2:

Пример:
3:

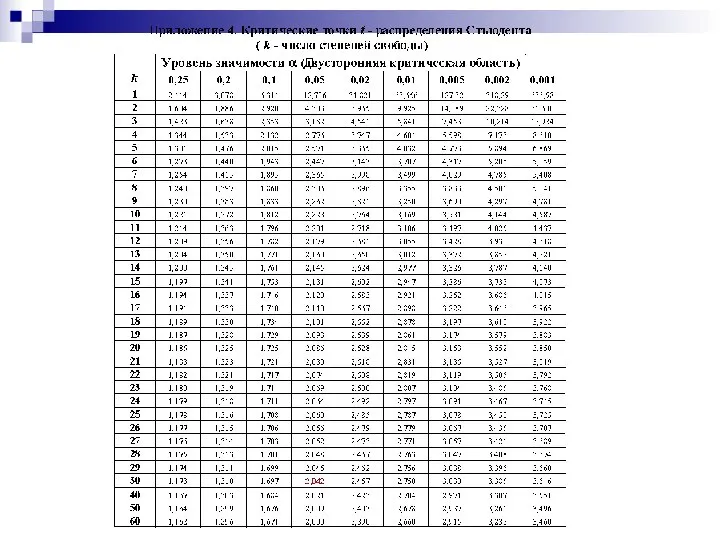
Доверительный интервал для оценки неизвестного математического ожидания нормально распределенной
случайной величины при неизвестном σ.

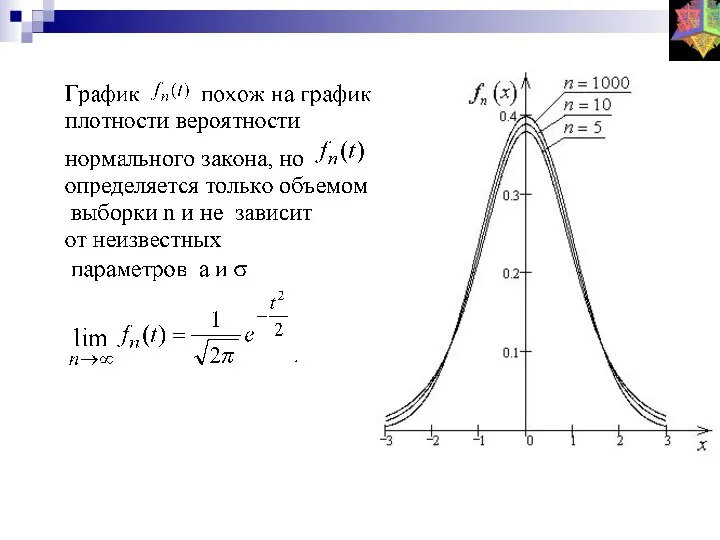
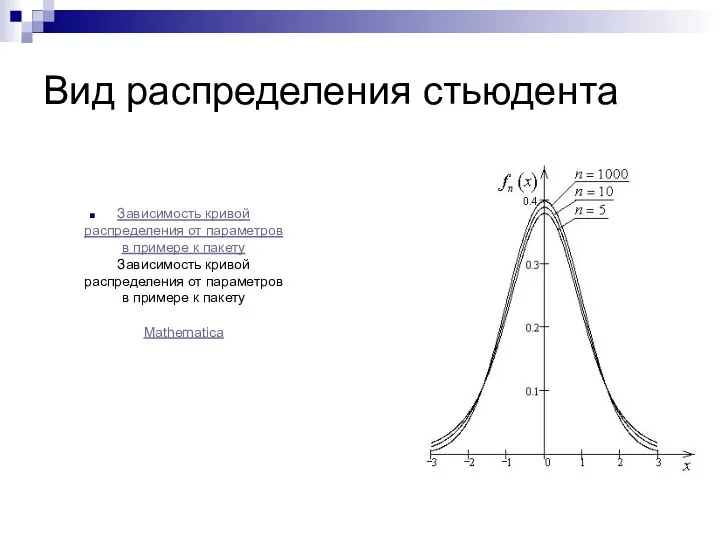
Вид распределения стьюдента
Зависимость кривой распределения от параметров в примере к пакету Зависимость кривой распределения от параметров в примере к пакету Mathematica

Распределение стьюдента

Пример:
3: