Слайд 2Закон тождества
Закон непротиворечия
Закон исключенного третьего
Закон двойного отрицания
Законы общей инверсии (законы де Моргана)
Закон

коммутативности
Закон ассоциативности
Закон дистрибутивности
Закон идемпотентности (равносильности)
Законы исключения констант
Законы поглощения
Законы исключения (склеивания)
Закон контрапозиции (правило перевертывания)
Выразить импликацию через конъюнкцию
Выразить эквивалентность через базовые логические операции
Слайд 3Закон тождества
Всякое высказывание тождественно самому себе
А = А

Слайд 4Закон непротиворечия
Высказывание не может быть одновременно истинным и ложным

Слайд 5Закон исключенного третьего
Высказывание может быть либо истинным, либо ложным, третьего не

дано.
Слайд 6Закон двойного отрицания
Если дважды отрицать некоторое высказывание, то в результате получим

исходное высказывание.
Слайд 7Законы общей инверсии (законы де Моргана)
Для логического сложения
Для логического умножения

Слайд 8Закон коммутативности (переместительный)
Для логического сложения
Для логического умножения

Слайд 9Закон ассоциативности (сочетательный)
Для логического сложения
Для логического умножения
Если в логическом выражении

используется только операция логического сложения или логического умножения, то можно пренебрегать скобками или расставлять их произвольно:
Слайд 10Закон дистрибутивности (распределительный)
Дистрибутивность сложения относительно умножения
Дистрибутивность умножения относительно сложения
В алгебре

высказываний можно выносить за скобки как общие множители, так и общие слагаемые.
Слайд 11 В обычной алгебре справедлив распределительный закон только для сложения:
(A+B)C=AC+BC

Слайд 12Закон идемпотентности (равносильности)
Для логического сложения
Для логического умножения

Слайд 13Законы исключения констант
Для логического сложения
Для логического умножения

Слайд 14Законы поглощения
Для логического сложения
Для логического умножения

Слайд 15Законы исключения (склеивания)
Для логического сложения
Для логического умножения

Слайд 16Закон контрапозиции (правило перевертывания)

Слайд 17Выразить импликацию через дизъюнкцию
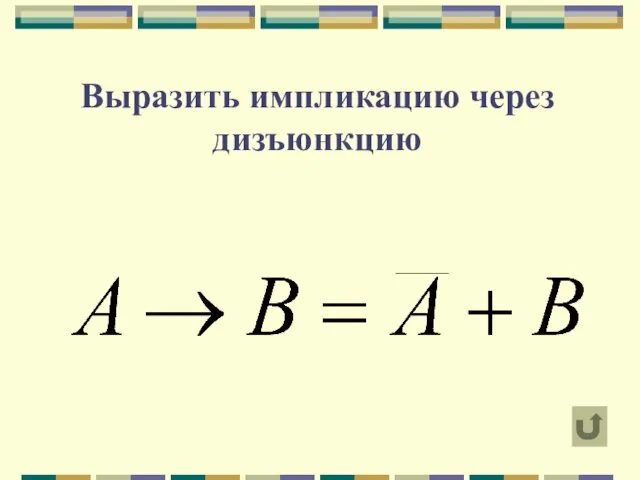















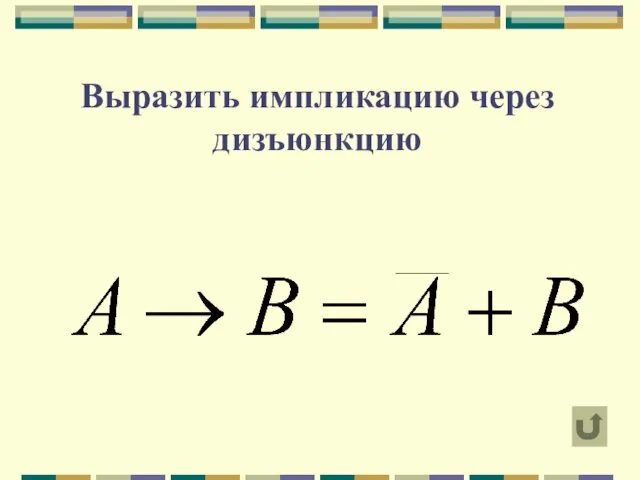
 Десятичные дроби
Десятичные дроби Преобразование формул
Преобразование формул Презентация на тему Великие русские математики
Презентация на тему Великие русские математики  Иррациональные уравнения
Иррациональные уравнения Угол
Угол Колесо истории математики
Колесо истории математики Интерактивный тренажёр. 4 класс
Интерактивный тренажёр. 4 класс Средняя линия треугольника
Средняя линия треугольника Приёмы устных вычислений
Приёмы устных вычислений Численные методы решения СЛАУ (часть 1)
Численные методы решения СЛАУ (часть 1) Преобразование графиков функции
Преобразование графиков функции Коэффициент. Числовой коэффициент
Коэффициент. Числовой коэффициент Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие Задания ГИА на нахождение площадей фигур, на выбор правильного утверждения
Задания ГИА на нахождение площадей фигур, на выбор правильного утверждения Основы моделирования
Основы моделирования Угол между прямой и плоскостью (Задание 13)
Угол между прямой и плоскостью (Задание 13) Устная работа на уроке геометрии
Устная работа на уроке геометрии Пифагор и его школа
Пифагор и его школа Методы общения линейных уравнений с тремя неизвестными
Методы общения линейных уравнений с тремя неизвестными Сечение многогранников. Применение интерактивных методов обучения на уроках математики
Сечение многогранников. Применение интерактивных методов обучения на уроках математики Анимированный плакат. Цифры-прописи
Анимированный плакат. Цифры-прописи Временные ряды
Временные ряды Методика проверки и оценки алгебраических заданий повышенного уровня сложности
Методика проверки и оценки алгебраических заданий повышенного уровня сложности Дифференциальные уравнения
Дифференциальные уравнения Эндогенность. Инструментальные переменные
Эндогенность. Инструментальные переменные Векторы. Нулевой вектор
Векторы. Нулевой вектор Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая геометрия Цилиндр. История возникновения
Цилиндр. История возникновения