Содержание
- 2. При дифференцировании мы искали производную по заданной функции y=F(x), то есть нужно было найти f(x)=F’(x). Можно
- 4. Определение: Дифференцируемая функция F(x) называется первообразной для функции f(x) на интервале (a,b), если F’(x)=f(x) на интервале
- 5. Первообразная для заданной функции f(x) существует только, если эта функция непрерывна на (a,b). Кроме того, первообразных
- 6. Определение: Выражение F(x)+C, где С - произвольная постоянная величина, определяющее множество первообразных для функции f(x), называется
- 7. Знак ∫ - знак неопределенного интеграла; f(x)dx – подынтегральное выражение; f(x) – подынтегральная функция.
- 8. Определение: Операция нахождения первообразной по заданной производной или дифференциалу называется интегрированием.
- 9. Интегрирование – действие, обратное дифференцированию. Его можно проверить дифференцированием, причем дифференцирование однозначно, а интегрирование дает ответ
- 10. Придавая постоянной величине С различные значения С1, С2, С3, получим различные функции y1(x)=F(x)+C1, y2(x)=F(x)+C2, y3(x)=F(x)+C3, каждая
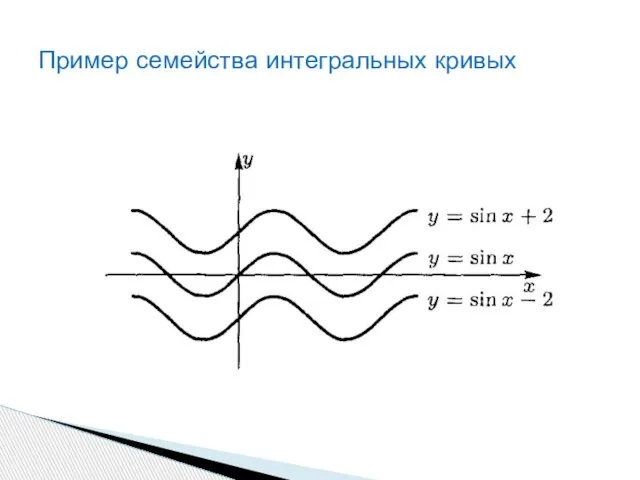
- 11. Следовательно, геометрически неопределенный интеграл представляет собой семейство интегральных кривых.
- 12. Пример семейства интегральных кривых
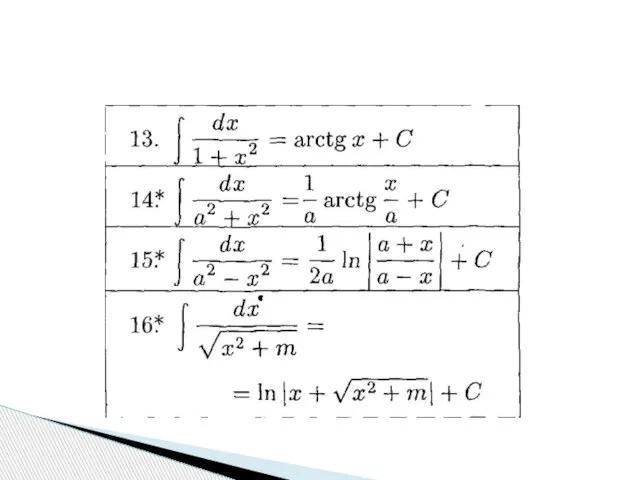
- 13. Чтобы находить первообразные, необходимо составить и выучить наизусть таблицу неопределенных интегралов от основных элементарных функций. Она
- 14. Таблица основных неопределенных интегралов
- 18. 1) Производная от неопределенного интеграла равна подынтегральной функции. 2. Свойства неопределенных интегралов
- 19. 2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
- 20. 3) Неопределенный интеграл от дифференциала функции равен этой функции, сложенной с произвольной постоянной:
- 21. 4) Постоянный множитель можно выносить за знак интеграла:
- 22. 5) Интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций:
- 23. Этот метод заключается в прямом использовании табличных интегралов и свойств. 3. Непосредственное интегрирование
- 24. Этот метод заключается в разложении подынтегральной функции в комбинацию более простых функций с использованием известных формул.
- 26. Таких методов два: а) метод замены переменной; б) интегрирование по частям. 3. Основные методы интегрирования
- 27. Метод основан на замене переменной в неопределенном интеграле с целью свести его нахождение к нахождению такого
- 28. Пример: Найти неопределенный интеграл: ∫cos2xdx Этот интеграл не является табличным. Произведем замену: y = 2x Тогда
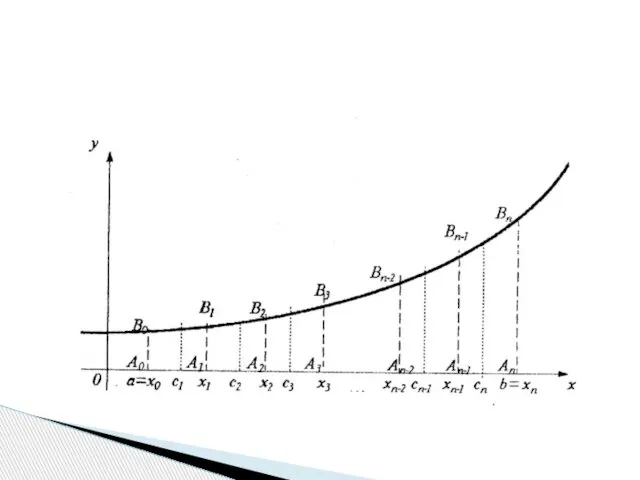
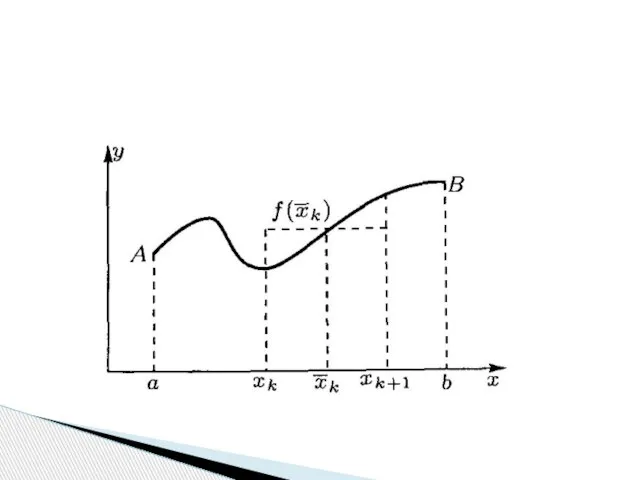
- 29. Рассмотрим некоторую непрерывную на конечном отрезке [a,b] функцию y=f(x). Разделим отрезок [a,b] на n частей (необязательно
- 31. Из точек деления восставим перпендикуляры к оси абсцисс до их пересечения с графиком функции в точках,
- 32. На каждом из отрезков [x0, x1], [x1, x2], [x2, x3], …, [xn-2, xn-1], [xn-1, xn] (эти
- 33. Составим сумму произведений значений функции y=f (x) в точках ci , где индекс i – номер
- 34. или, в сокращенной записи
- 35. где символ означает суммирование по индексу i , последовательно изменяющемуся от 1 до n включительно.
- 36. Сумма In называется интегральной суммой функции y=f(x) на отрезке [a,b].
- 37. Определение: Если существует конечный предел интегральной суммы функции y=f(x) на отрезке [a,b] при стремлении к 0
- 39. Функция f(x) – подынтегральная функция, x – переменная интегрирования. Числа a и b (границы отрезка [a,b])
- 40. Неопределенный интеграл – это семейство первообразных функций; Определенный интеграл – число! Основное отличие определенного интеграла от
- 41. Определенный интеграл равен площади криволинейной трапеции, т.е. плоской фигуры, ограниченной сверху графиком непрерывной функции у= f(x)
- 43. 5. Свойства определенного интеграла
- 46. Формулу называют формулой Ньютона-Лейбница.
- 48. 6. Основные методы вычисления определенных интегралов
- 50. Обратите внимание: 1) при замене переменной соответствующим образом изменяют и пределы интегрирования (cos 0 = 1;
- 52. Скачать презентацию

























![Рассмотрим некоторую непрерывную на конечном отрезке [a,b] функцию y=f(x). Разделим отрезок [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/838351/slide-28.jpg)

![На каждом из отрезков [x0, x1], [x1, x2], [x2, x3], …, [xn-2,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/838351/slide-31.jpg)



![Сумма In называется интегральной суммой функции y=f(x) на отрезке [a,b].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/838351/slide-35.jpg)
![Определение: Если существует конечный предел интегральной суммы функции y=f(x) на отрезке [a,b]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/838351/slide-36.jpg)
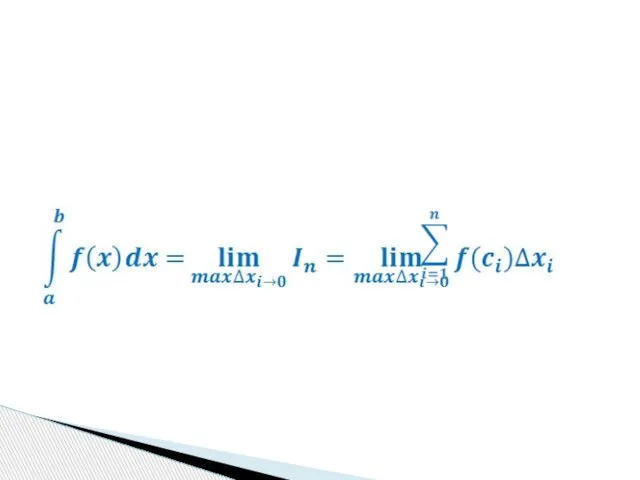







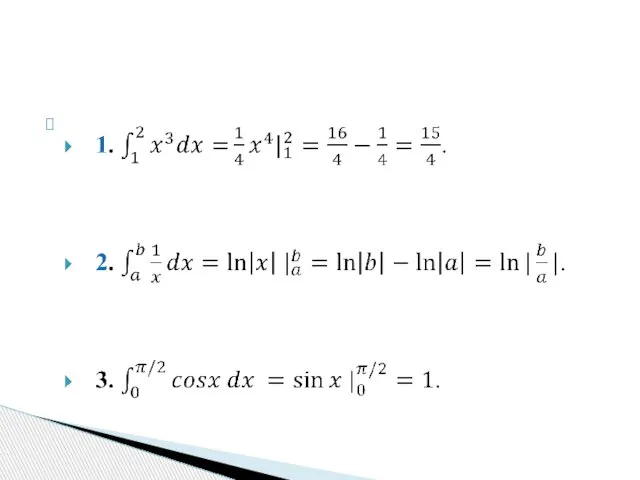



 Смысл умножения. Тренажер
Смысл умножения. Тренажер Прямые и плоскости в пространстве
Прямые и плоскости в пространстве Окружность в аксонометрии. 8 класс
Окружность в аксонометрии. 8 класс Задачи на построение
Задачи на построение Путешествие в город Дробей на проспект Умножения. 6 класс
Путешествие в город Дробей на проспект Умножения. 6 класс Презентация на тему Устный счет до десяти
Презентация на тему Устный счет до десяти  Решение тригонометрических уравнений
Решение тригонометрических уравнений Правила вычисления производных
Правила вычисления производных Забавные фигуры. Занятие с дошкольниками
Забавные фигуры. Занятие с дошкольниками Случайные события
Случайные события Правильный многоугольник
Правильный многоугольник Комбинаторная задача с монетами
Комбинаторная задача с монетами Применение мультимедийных презентаций для изучения геометрического материала на уроках математики в 5-6 классах. Модуль 3
Применение мультимедийных презентаций для изучения геометрического материала на уроках математики в 5-6 классах. Модуль 3 Возникновение слова “процент”. Древний Рим
Возникновение слова “процент”. Древний Рим Показательная функция
Показательная функция Методы кластеризации
Методы кластеризации Решение задач на готовых чертежах. Геометрия. 9 класс
Решение задач на готовых чертежах. Геометрия. 9 класс Решение систем линейных уравнений способом подстановки
Решение систем линейных уравнений способом подстановки Презентация на тему Площадь трапеции 8 класс
Презентация на тему Площадь трапеции 8 класс  Презентация на тему Все о треугольниках
Презентация на тему Все о треугольниках  Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число
Путешествие по родному краю. Курильский заповедник. Выбери наибольшее число Точечные и интервальные оценки
Точечные и интервальные оценки Для чего нужна математика?
Для чего нужна математика? ВКР: Исследование нормального строения конечных групп
ВКР: Исследование нормального строения конечных групп ОГЭ 2019. Модуль Геометрия
ОГЭ 2019. Модуль Геометрия Математика
Математика Выполни цепочку
Выполни цепочку Кривые второго порядка гипербола и парабола
Кривые второго порядка гипербола и парабола