Аксиомы стереометрии и их следствия

Изучает свойства геометрических фигур на плоскости
Изучает свойства фигур в пространстве
В переводе с греческого слово «геометрия» означает «землемерие»
«гео» – по-гречески земля, «метрео» – мерить
Слово «стереометрия» происходит от греческих слов «стереос» объемный, пространственный, «метрео» – мерить
Изучение нового материала.

Планиметрия
Стереометрия
Наряду с этими фигурами мы будем рассматривать геометрические тела и их поверхности.
Например, многогранники. Куб, параллелепипед, призма, пирамида.
Тела вращения.
Шар, сфера, цилиндр, конус.
Основные фигуры: точка, прямая
Основные фигуры: точка, прямая, плоскость
Другие фигуры: отрезок, луч, треугольник, квадрат, ромб, параллелограмм, трапеция, прямоугольник, выпуклые и невыпуклые n-угольники, круг, окружность, дуга и др.
Изучение нового материала.

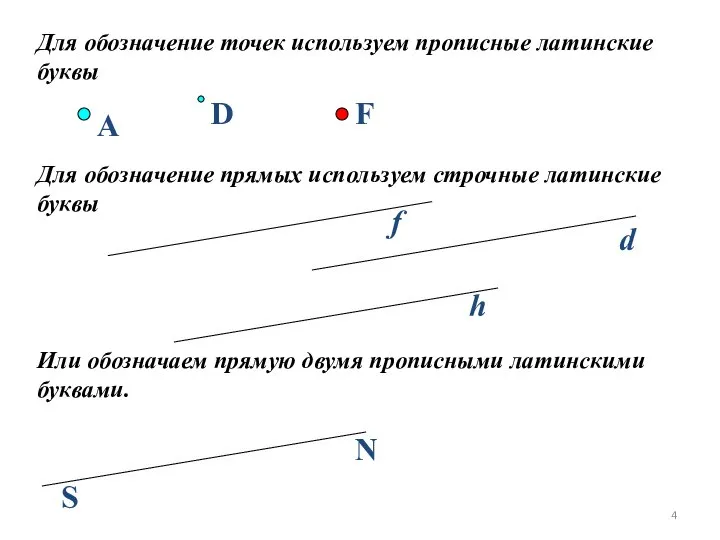
Для обозначение точек используем прописные латинские буквы
Для обозначение прямых используем строчные латинские буквы
Или обозначаем прямую двумя прописными латинскими буквами.

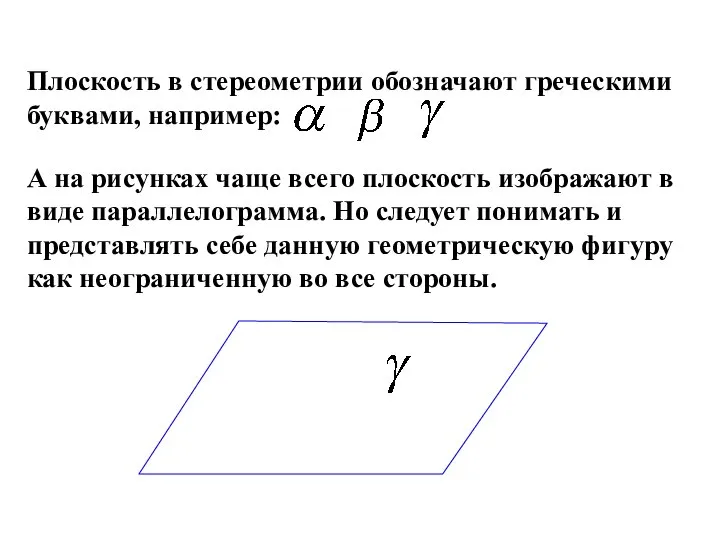
Плоскость в стереометрии обозначают греческими буквами, например:
А на рисунках чаще всего плоскость изображают в виде параллелограмма. Но следует понимать и представлять себе данную геометрическую фигуру как неограниченную во все стороны.

ОБОЗНАЧЕНИЯ
Точка A принадлежит прямой a
Точка B не принадлежит прямой a

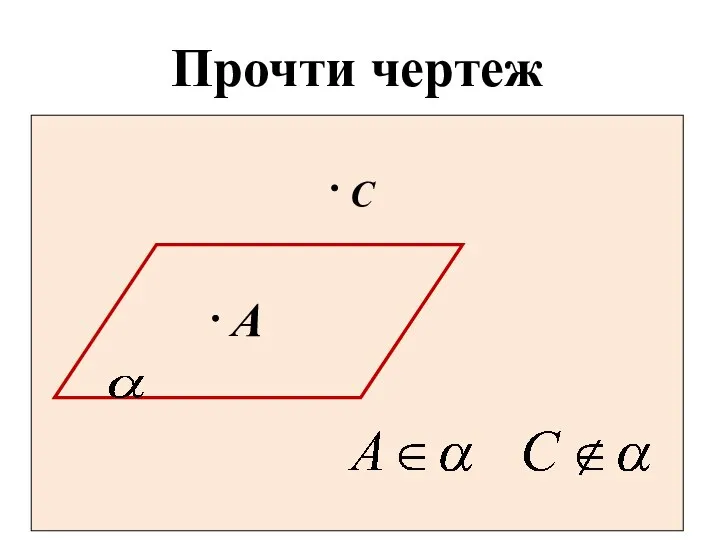
Прочти чертеж
A
С

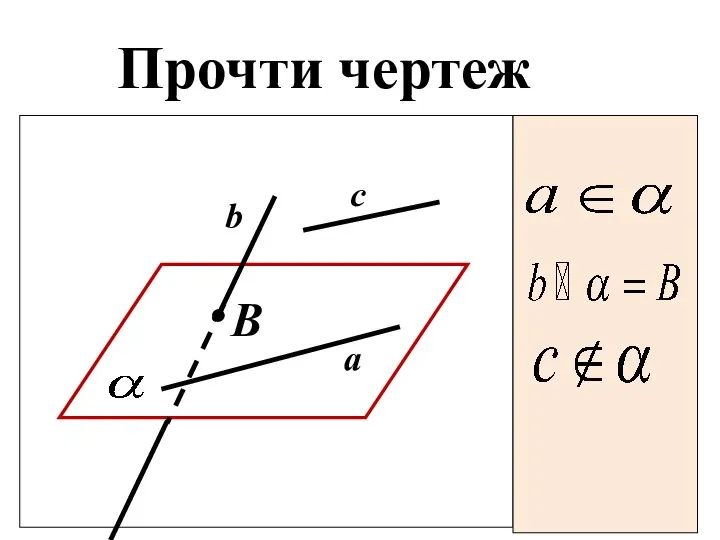
Прочти чертеж
B
c
b
a

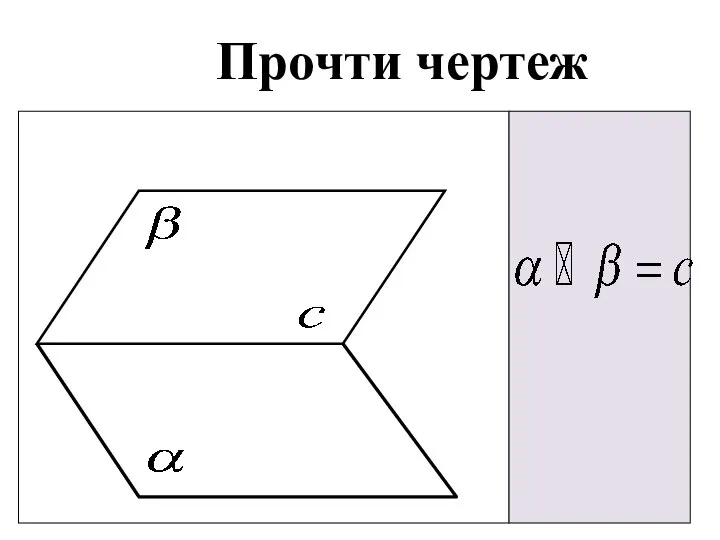
Прочти чертеж

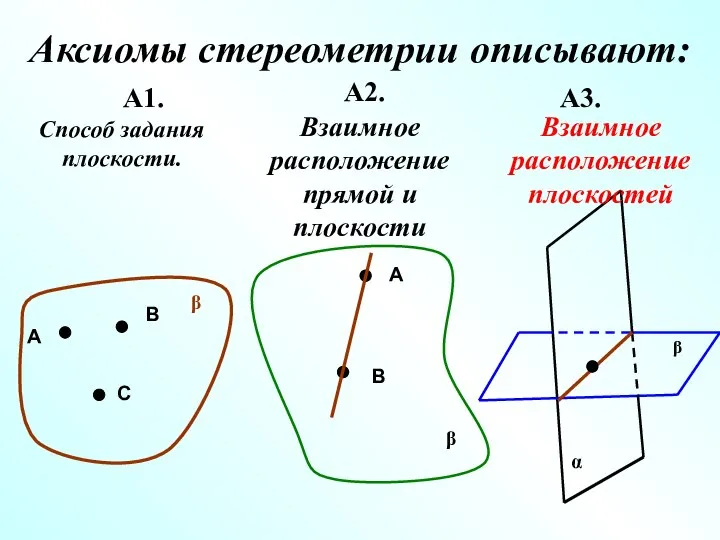
Аксиомы стереометрии описывают:
А1.
А2.
А3.
А
В
С
β
Способ задания плоскости.
β
А
В
Взаимное расположение прямой и плоскости
α
β
Взаимное расположение плоскостей

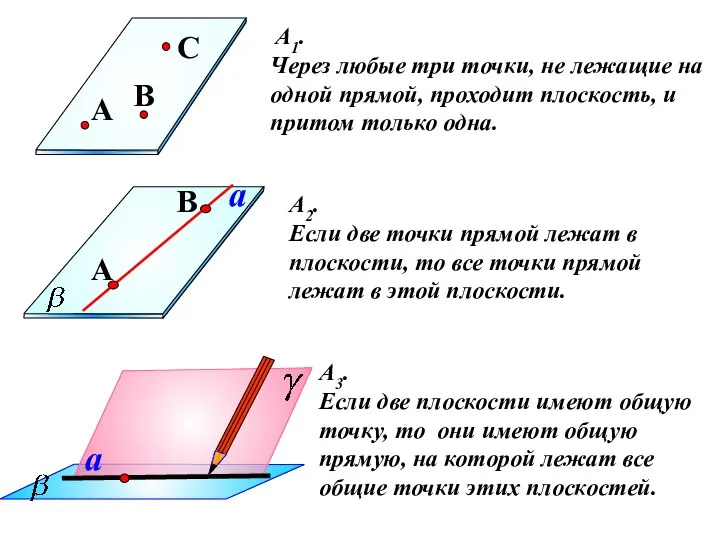
А1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

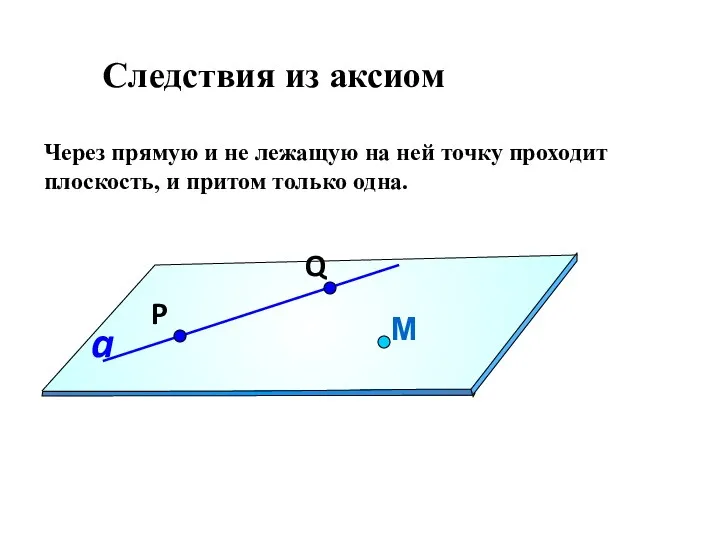
Следствия из аксиом
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
М
a

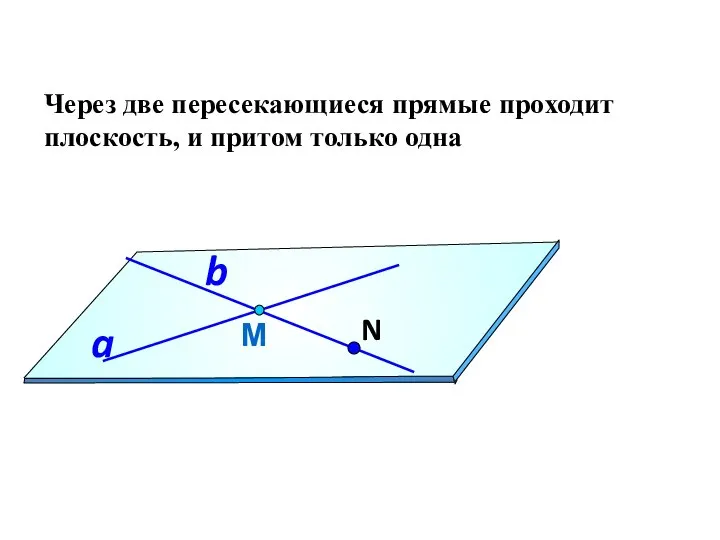
Через две пересекающиеся прямые проходит плоскость, и притом только одна
М
a
b
N

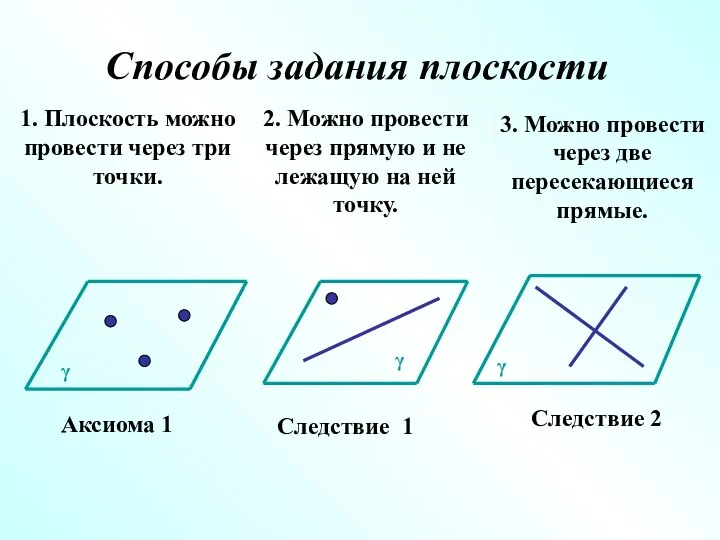
Способы задания плоскости
1. Плоскость можно провести через три точки.
2. Можно провести через прямую и не лежащую на ней точку.
Аксиома 1
Следствие 1
Следствие 2
3. Можно провести через две пересекающиеся прямые.

Определите: верно, ли суждение?
Любые три точки лежат в одной плоскости.
Любые четыре точки лежат в одной плоскости.
Любые четыре точки не лежат в одной плоскости.
Через любые три точки проходит плоскость и при том только одна.
Если прямая пересекает 2 стороны треугольника, то она лежит в плоскости треугольника.
Если прямая проходит через вершину треугольника, то она лежит в плоскости треугольника.
Если прямые не пересекаются, то они параллельны.
Если плоскости не пересекаются, то они параллельны.
В стереометрии мы будем рассматривать ситуации, задающие различные расположения в пространстве основных фигур относительно друг друга
ДА
ДА
ДА
НЕТ
НЕТ
НЕТ
НЕТ
НЕТ

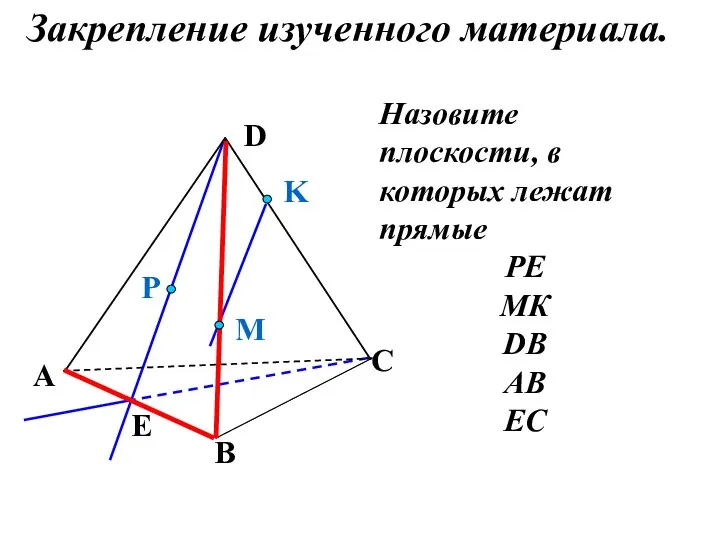
Назовите плоскости, в которых лежат прямые
РЕ
МК
DB
AB
EC
P
E
A
B
C
D
M
K
Закрепление изученного материала.

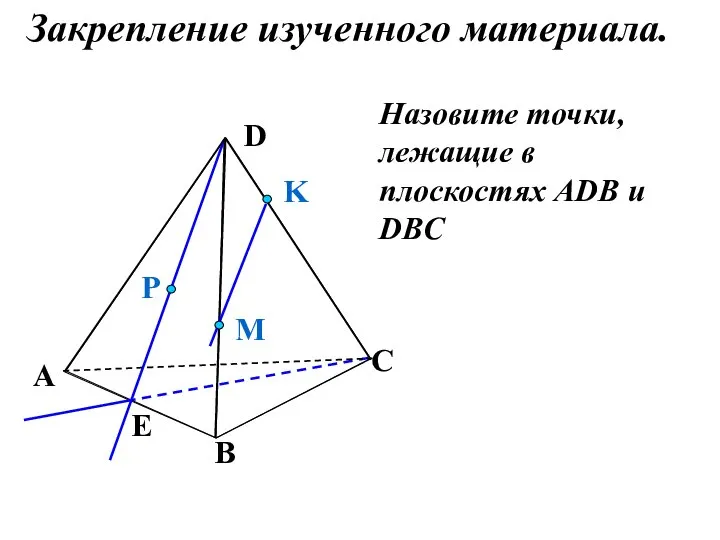
Назовите точки, лежащие в плоскостях АDB и DBC
P
E
A
B
C
D
M
K
Закрепление изученного материала.

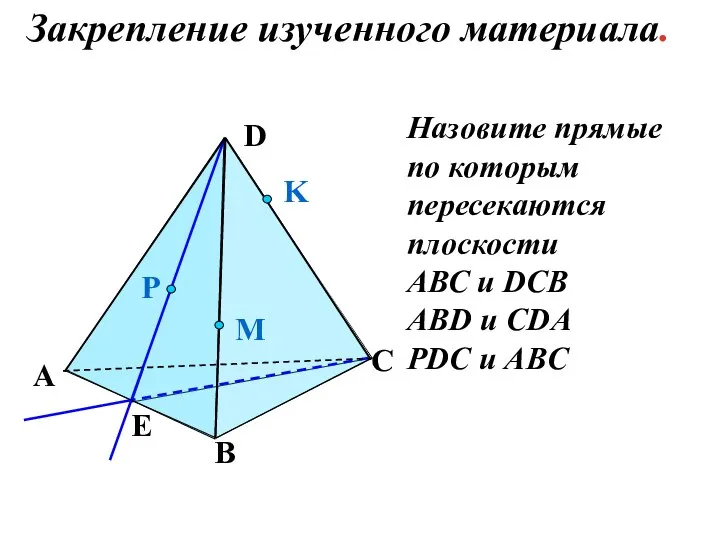
Назовите прямые по которым пересекаются плоскости
АВС и DCB
ABD и CDA
PDC и ABC
P
E
A
B
C
D
M
K
Закрепление изученного материала.

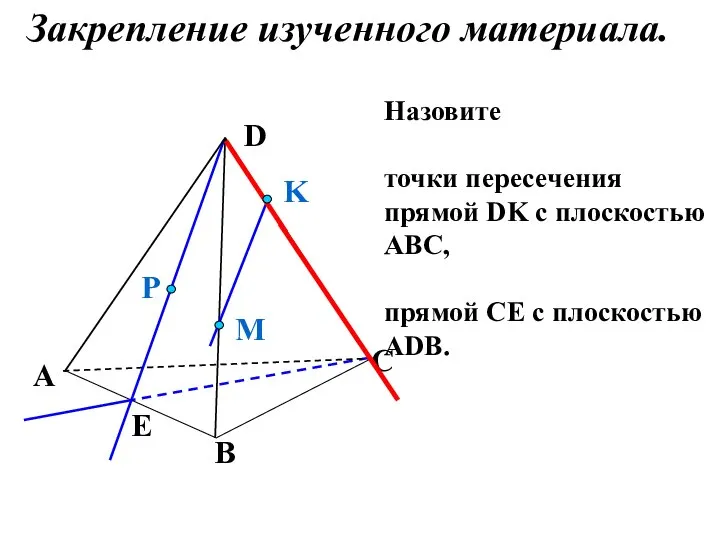
Назовите
точки пересечения прямой DK с плоскостью АВС,
прямой СЕ с плоскостью АDB.
P
E
A
B
C
D
M
K
Закрепление изученного материала.

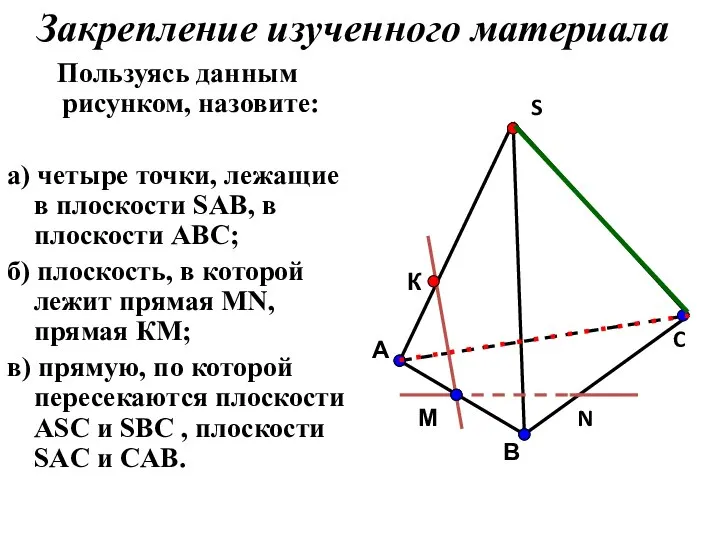
Пользуясь данным рисунком, назовите:
а) четыре точки, лежащие в плоскости SAB, в плоскости АВС;
б) плоскость, в которой лежит прямая MN, прямая КМ;
в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.
Закрепление изученного материала

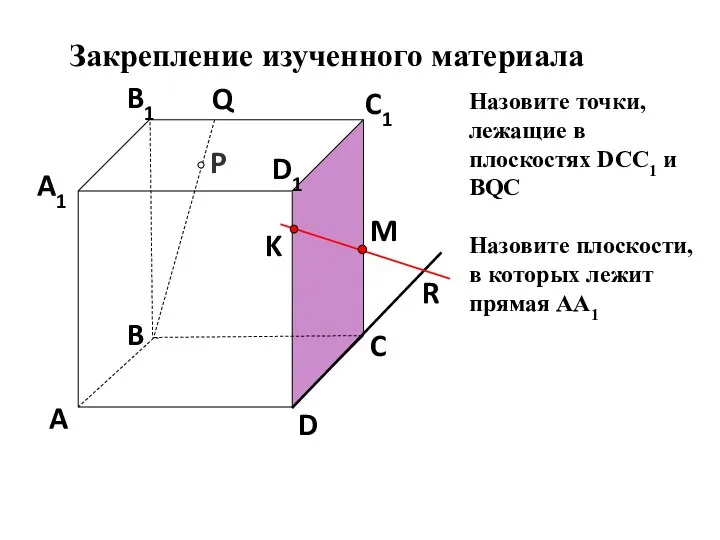
P
A
B
C
D
A1
B1
C1
D1
R
M
K
Q
Назовите точки, лежащие в плоскостях DCC1 и BQC
Назовите плоскости, в которых лежит прямая АА1
Закрепление изученного материала

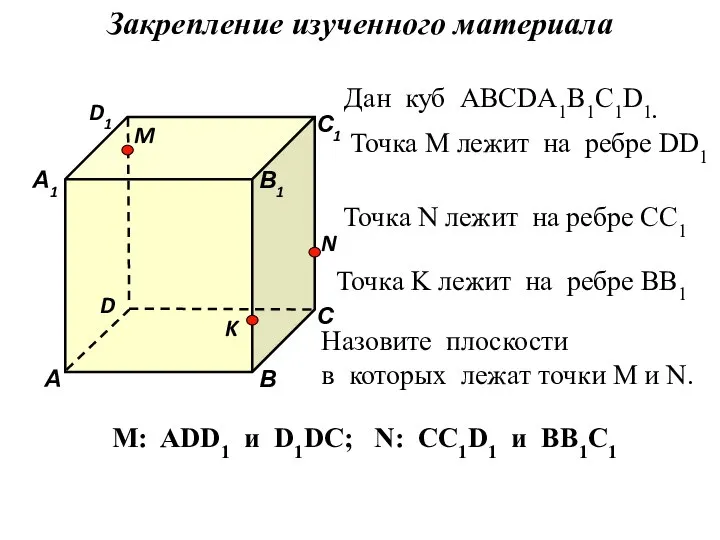
Дан куб АВСDA1B1C1D1.
Точка М лежит на ребре DD1
Точка N лежит на ребре CC1
Точка K лежит на ребре BB1
D1
В
А1
А
D
С1
С
В1
M
N
K
Назовите плоскости
в которых лежат точки М и N.
M: ADD1 и D1DC; N: CC1D1 и BB1C1
Закрепление изученного материала

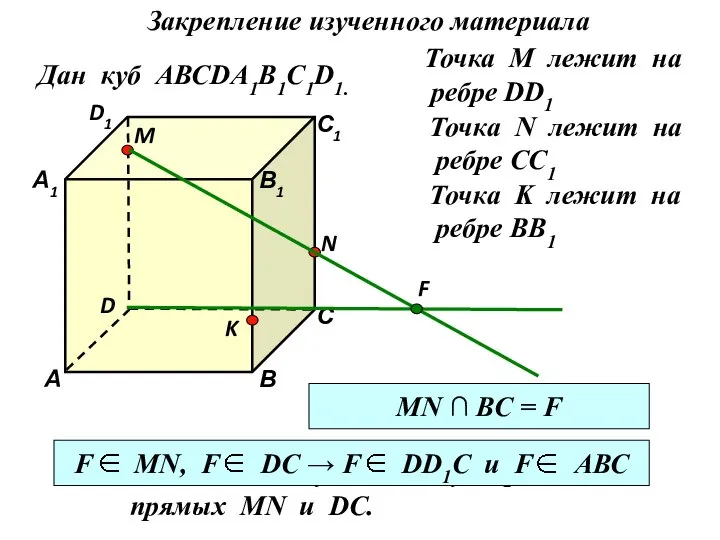
Дан куб АВСDA1B1C1D1.
D1
D
С1
С
В1
В
А1
А
M
Точка М лежит на
ребре DD1
N
Точка N лежит на
ребре CC1
K
Точка K лежит на
ребре BB1
2) Найдите точку F – точку пересечения
прямых MN и DС.
F
Каким свойством обладает точка F?
MN ∩ BC = F
F MN, F DC → F DD1C и F АВС
Закрепление изученного материала