Содержание
- 2. 1) Например, в теории межпланетных путешествий решается задача об определении массы топлива, необходимого для того, чтобы
- 3. 2) Радиоактивный распад вещества задаётся формулой m = m0(1/2)t/tо, где m и mо – масса радиоактивного
- 4. 3) Изменение атмосферного давления p в зависимости от высоты h над уровнем моря описывается формулой p
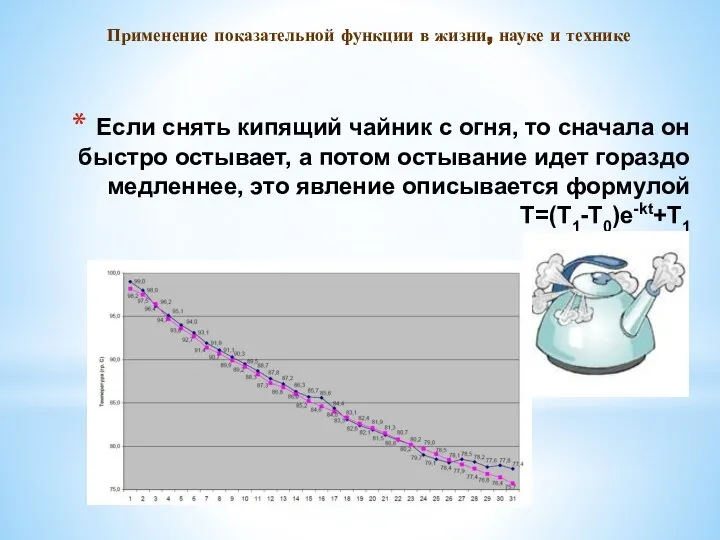
- 5. Если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо
- 6. Рост народонаселения Изменение числа людей в стране на небольшом отрезке времени описывается формулой , где N0
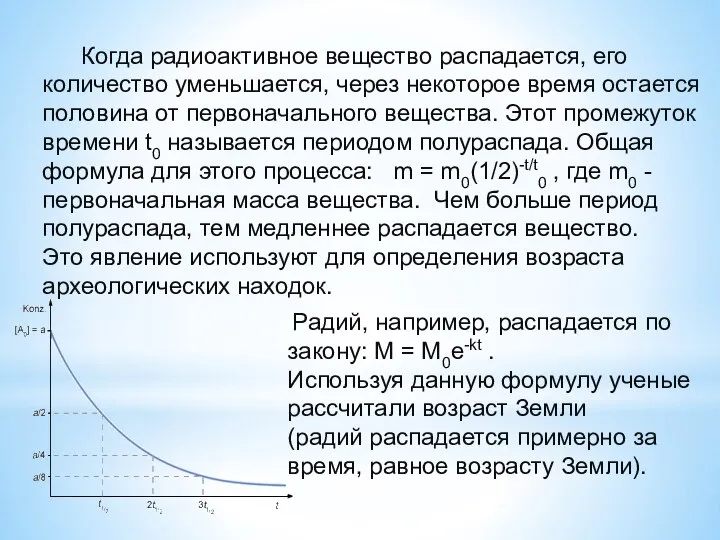
- 7. Когда радиоактивное вещество распадается, его количество уменьшается, через некоторое время остается половина от первоначального вещества. Этот
- 8. Определение Показательная функция – это функция вида , где x – переменная, - заданное число, >0,
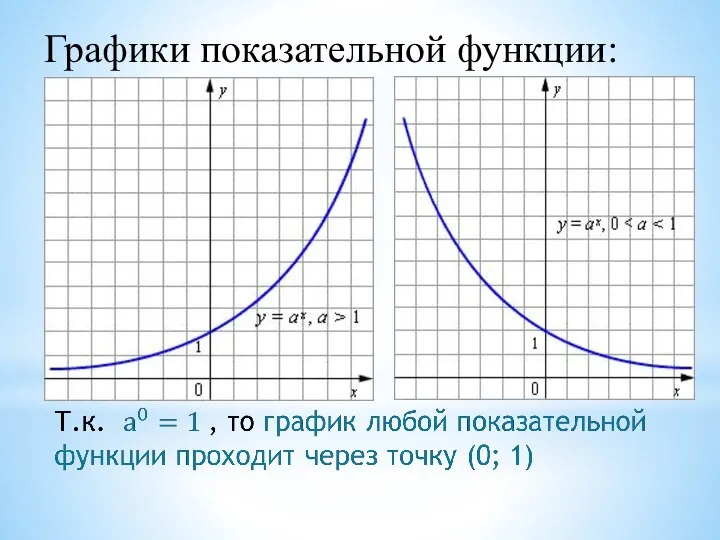
- 9. Область определения показательной функции: D (y)=R – множество всех действительных чисел. Область значений показательной функции: E
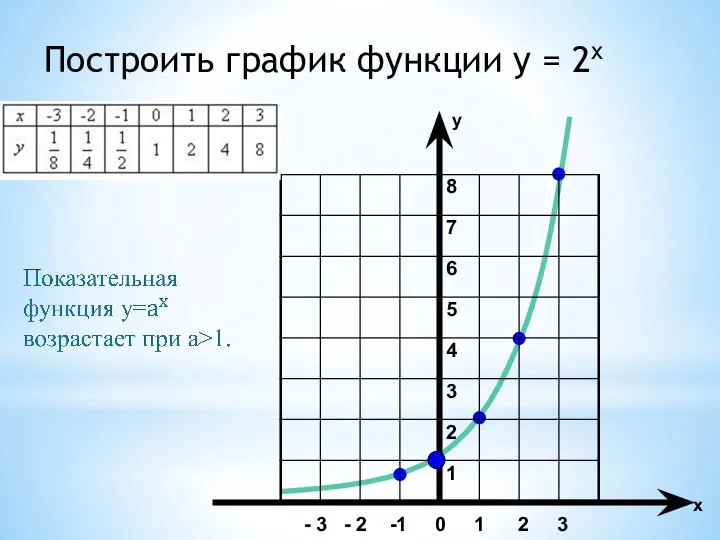
- 10. Построить график функции y = 2x 8 7 6 5 4 3 2 1 - 3
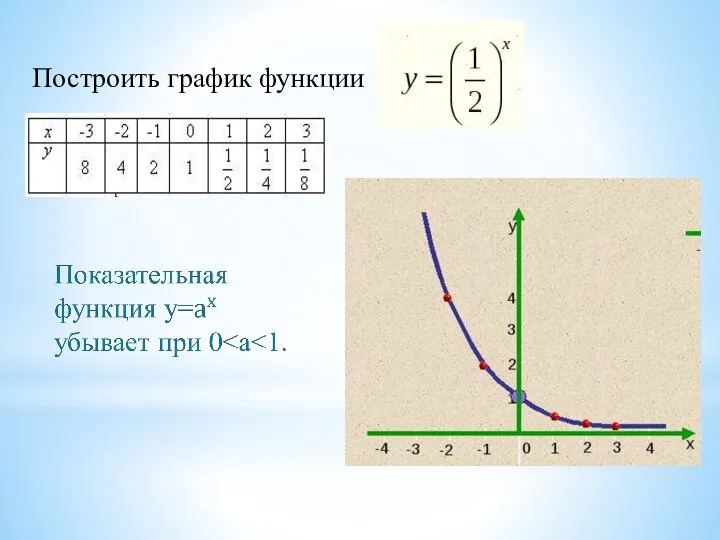
- 11. Построить график функции
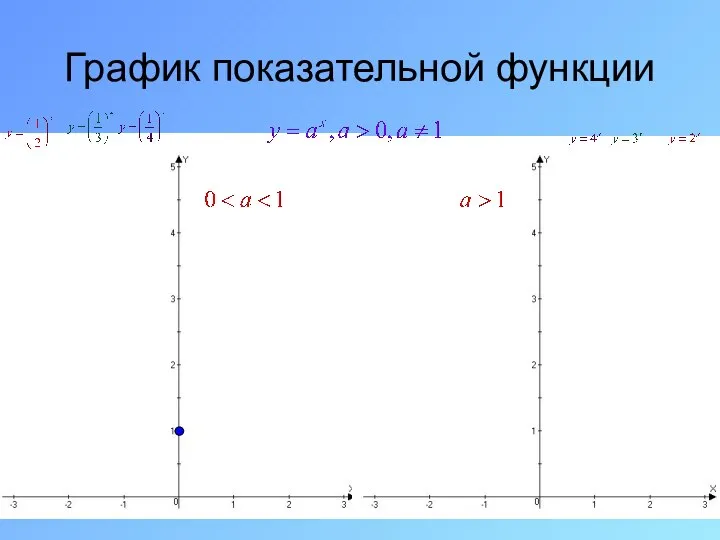
- 12. Графики показательной функции:
- 13. Точек экстремума xmax и xmin нет. Экстремумов уmax и уmin нет. Не является ни четной, ни
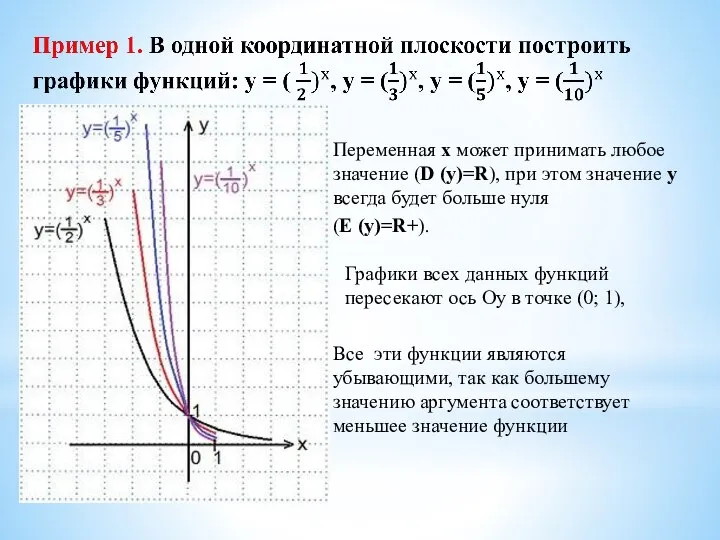
- 14. Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля
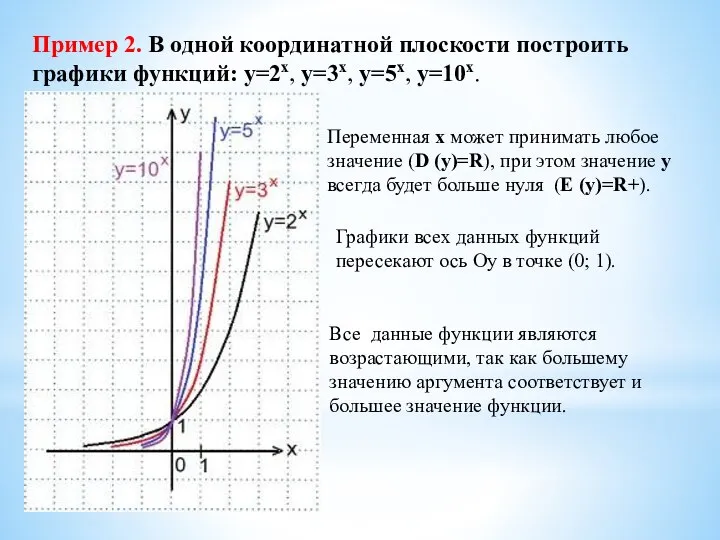
- 15. Пример 2. В одной координатной плоскости построить графики функций: y=2x, y=3x, y=5x, y=10x. Переменная х может
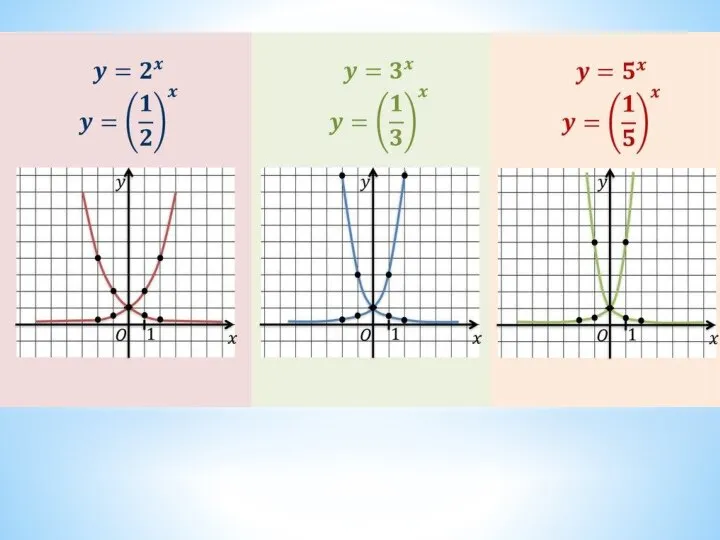
- 17. График показательной функции
- 18. Задание A1 Из предложенного списка функций, выбрать ту функцию, которая является показательной:
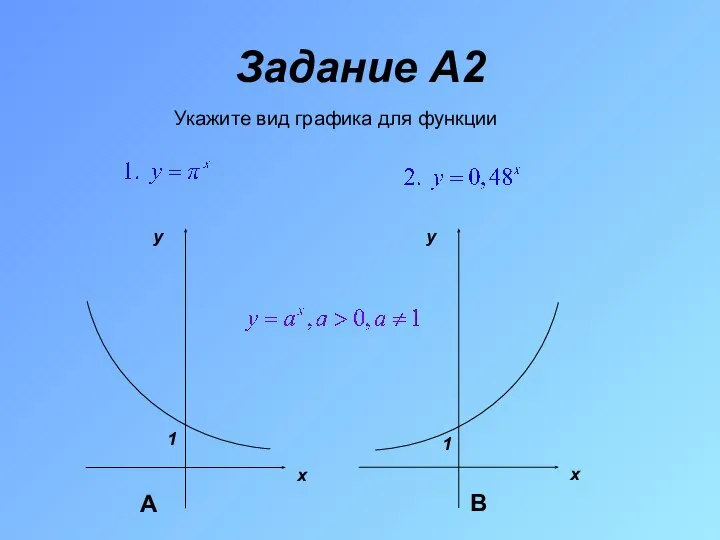
- 19. Задание A2 Укажите вид графика для функции А В
- 20. Задание A3 Дан график функции. Укажите эту функцию.
- 21. Задание A4 Выберите функцию возрастающую на
- 22. Задание A5 Выберите функцию убывающую на
- 23. Задание A6 Решите уравнения
- 24. Задание В1 Укажите область значений функции
- 25. Задание В2 Какое из указанных чисел входит в область значений функции Для любого Решение: Ответ: 5.
- 27. Показательная функция Сравнение чисел с использованием свойств показательной функции Сравнение числа с 1 а) аналитический способ;
- 28. Задача 1 Сравнить числа Решение Ответ:
- 29. Задача 2 Сравнить число с 1. Решение -5 Ответ:
- 30. Используя свойства возрастания и убывания показательной функции сравнить числа: Сравнить: а) 53 и 55; б) 47
- 32. Скачать презентацию



















 Цилиндр, конус, шар
Цилиндр, конус, шар Формулы сложения
Формулы сложения Решение логических задач
Решение логических задач Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Статистическая обработка измерений
Статистическая обработка измерений Экономическая статистика. Демография предприятий
Экономическая статистика. Демография предприятий Понятие многогранника
Понятие многогранника Щенок Пузырёк. Сложение и вычитание в пределах десяти
Щенок Пузырёк. Сложение и вычитание в пределах десяти Математические ребусы. 4 класс
Математические ребусы. 4 класс Преобразование графиков функций
Преобразование графиков функций Презентация на тему Признаки равенства и подобия треугольников
Презентация на тему Признаки равенства и подобия треугольников  Окружность
Окружность Центральные и вписанные углы
Центральные и вписанные углы Ряды
Ряды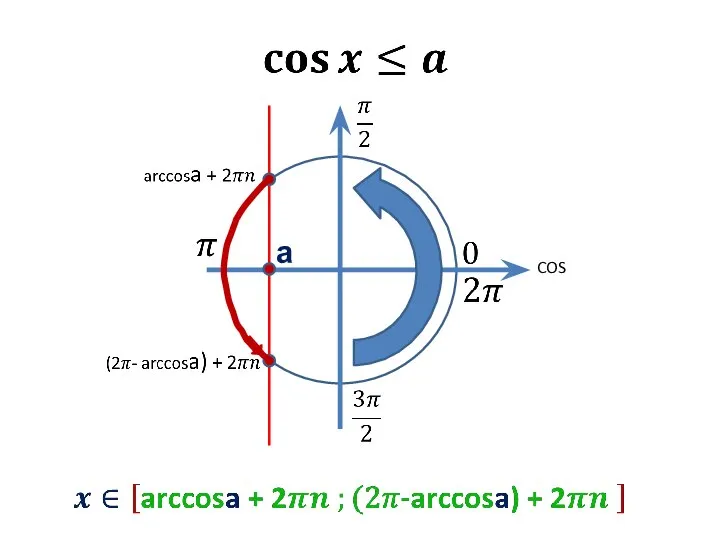 Неравенства вида Cos〖x≤a〗
Неравенства вида Cos〖x≤a〗 Устная работа. Разложите на множители
Устная работа. Разложите на множители обратные тригонометрические функции
обратные тригонометрические функции Логарифмические неравенства
Логарифмические неравенства Решение задач по теме: Четырехугольники
Решение задач по теме: Четырехугольники Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах
Распространение электромагнитных волн в анизотропных средах. Двойное лучепреломление в кристаллах Презентация на тему Решение систем неравенств (8 класс)
Презентация на тему Решение систем неравенств (8 класс)  Презентация на тему Исследование функции и построение графика (10 класс)
Презентация на тему Исследование функции и построение графика (10 класс)  Нахождение точек экстремума функции. 10 класс
Нахождение точек экстремума функции. 10 класс Поворот. Пример построения треугольника
Поворот. Пример построения треугольника Оснащение математических уголков в ДОУ
Оснащение математических уголков в ДОУ Математика ЕГЭ 2018 №7
Математика ЕГЭ 2018 №7 Дифференциальные уравнения. Лекция 2
Дифференциальные уравнения. Лекция 2 Сложение чисел с переходом через десяток в пределах 20. Помоги русалке
Сложение чисел с переходом через десяток в пределах 20. Помоги русалке