Слайд 2Актуальность и цели работы
В последнее время возрос интерес к разработке асимптотических методов

нелинейной динамики. Имеется потребность в методах, способных находить точные решения дифференциально разностных уравнений (ДРУ) и систем ДРУ. В работе рассмотрен метод геометрических рядов.
Целью данной работы является описание данного метода и его применение к некоторым широко известным уравнениям.
Слайд 3Метод получения точного решения на примере уравнения Бюргерса

Слайд 4Метод получения точного решения на примере уравнения Бюргерса

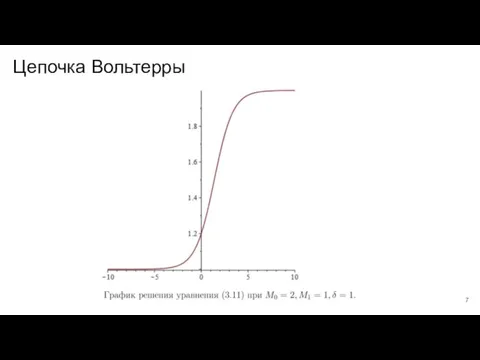
Слайд 5Цепочка Вольтерры
Переход к уравнению бегущей волны
Ищем решение в виде экспоненциального ряда функций

с неизвестными коэффициентами
Следовательно
Слайд 6Цепочка Вольтерры
Получим степенной ряд по переменной Z:
Далее осуществляется проверка, что ряд является

геометрическим, путем вычисления для него нескольких первых диагональных аппроксимант Паде: [13]:
Слайд 8Модифицированное дискретное уравнение Савада-Котера
Перейдя к текущей переменной получим:
Применяя те же преобразования что

и в предыдущем случае, собирая по степеням экспоненциальной функции и приравнивая к нулю коэффициент при eZ, получаем:
Слайд 9Модифицированное дискретное уравнение Савада-Котера
Как и в предыдущем случае, последовательно приравнивая коэффициенты при

e2z,e3z.. к нулю находим коэффициенты M2,M3, ... после замены eZ=Z ряд принимает форму
Расчет аппроксимаций Паде показывает, что [1/1] = [2/2], [2/2]= [3/3]. После обратной замены Z=eZ, аппроксиманта
становится точным решением уравнения.
Слайд 10Модифицированное дискретное уравнение Савада-Котера
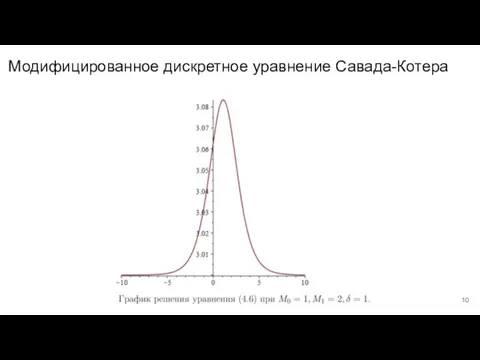








 Окружность и круг
Окружность и круг Решение задач с помощью уравнений. Алгебра. 7 класс. Ю.М. Колягин и др
Решение задач с помощью уравнений. Алгебра. 7 класс. Ю.М. Колягин и др Матрицы и определители
Матрицы и определители Первое знакомство с понятием вероятность. Урок 146
Первое знакомство с понятием вероятность. Урок 146 Презентация на тему Умножаем и делим на 10, 100, 1000 (3 класс)
Презентация на тему Умножаем и делим на 10, 100, 1000 (3 класс)  Проценты. Задачи на концентрацию, сплавы. ЕГЭ В11
Проценты. Задачи на концентрацию, сплавы. ЕГЭ В11 Решение задач по теме Теорема Пифагора и площади фигур. 8 класс
Решение задач по теме Теорема Пифагора и площади фигур. 8 класс L_3
L_3 Неопределенные интегралы
Неопределенные интегралы Самостоятельная работа по математике
Самостоятельная работа по математике Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Методы решения логических задач
Методы решения логических задач Целое уравнение
Целое уравнение Презентация на тему Умножение двузначного числа на однозначное (3 класс)
Презентация на тему Умножение двузначного числа на однозначное (3 класс)  Градусное измерение углов. Сумма углов в треугольнике. Тест
Градусное измерение углов. Сумма углов в треугольнике. Тест dispersionnyy-analiz(1)
dispersionnyy-analiz(1) Прямая и плоскость в пространстве. Лекция 6
Прямая и плоскость в пространстве. Лекция 6 Многоугольники в жизни
Многоугольники в жизни парні і непарні функції-1
парні і непарні функції-1 Сантиметр - единица измерения длины
Сантиметр - единица измерения длины Факториал
Факториал ОГЭ 2020-21. Задание №9. Найдите корень уравнения
ОГЭ 2020-21. Задание №9. Найдите корень уравнения Ряды
Ряды Правильные многоугольники
Правильные многоугольники Граница круга
Граница круга Теорема Пифагора
Теорема Пифагора Сравнение выражений
Сравнение выражений Презентация на тему Транспортир. Измерение углов транспортиром
Презентация на тему Транспортир. Измерение углов транспортиром