появление другого в одном и том же испытании.
Пример. Испытание: оценка за урок.
Решение. Х-учитель поставил за урок 2. Y-учитель поставил за урок 5. X и Y несовместимые, так как появление одного из них исключает появление другого.
Несовместимость более двух событий означает их попарную несовместимость.
Пример. Испытание: однократное бросание игральной кости.
Решение. Пусть события Х1, Х2, Х3, Х4, Х5, Х6-соответственно выпадение одного очка, двух, трех, четырех, пяти и шести. Эти события попарно несовместимы.





 Презентация на тему Геометрическая прогрессия и ее свойство
Презентация на тему Геометрическая прогрессия и ее свойство  Трикутники
Трикутники Перпендикуляр и наклонная к плоскости. Решение задач
Перпендикуляр и наклонная к плоскости. Решение задач Презентация на тему Иррациональные числа (8 класс)
Презентация на тему Иррациональные числа (8 класс)  Тригонометрия. Математическая игра АС-11
Тригонометрия. Математическая игра АС-11 Презентация на тему Сдвиг графика функции y = x вдоль осей координат
Презентация на тему Сдвиг графика функции y = x вдоль осей координат  Отображение. Отражение относительно прямой. Преобразование единичного квадрата
Отображение. Отражение относительно прямой. Преобразование единичного квадрата Решение задач
Решение задач Старинные меры массы и длины
Старинные меры массы и длины Скалярное произведение векторов
Скалярное произведение векторов Волшебный треугольник
Волшебный треугольник Тела вращения
Тела вращения Равнобедренный треугольник
Равнобедренный треугольник Пифагор и литература
Пифагор и литература Решение примеров и простых задач в пределах 10
Решение примеров и простых задач в пределах 10 Заниматика. Миром управляют числа
Заниматика. Миром управляют числа Случайные процессы с дискретными состояниями
Случайные процессы с дискретными состояниями Параллельные прямые
Параллельные прямые Lecture 6. Techniques of Integration (part 1)
Lecture 6. Techniques of Integration (part 1) Аналитическая панель
Аналитическая панель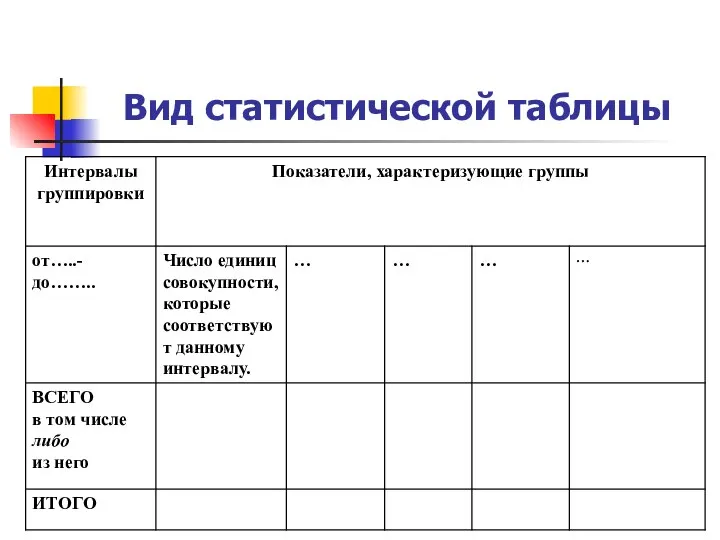 Вид статистической таблицы
Вид статистической таблицы Случаи сложения вида +7
Случаи сложения вида +7 Усеченная пирамида
Усеченная пирамида График равномерного движения
График равномерного движения Задачи на проценты. Схемы
Задачи на проценты. Схемы Многогранники в нашей жизни
Многогранники в нашей жизни Прямоугольный параллелепипед. Урок обобщения и систематизации знаний
Прямоугольный параллелепипед. Урок обобщения и систематизации знаний Презентация на тему Комбинации шара с многогранниками и фигурами вращения
Презентация на тему Комбинации шара с многогранниками и фигурами вращения