Содержание
- 3. y=-f(x) y=f(-x) y=f(x)+a y=f(x+a) y=a·f(x) y=f(a·x) y=|f(x)| y=f(|x|) Содержание
- 4. Если известен график функции y=f(x), то с помощью некоторых преобразований плоскости (параллельный перенос, осевая и центральная
- 5. График этой функции получается путём симметричного отображения графика y=f(x) относительно оси x. Замечание: точки пересечения графика
- 6. y y=2x y=-2x x Примеры: x x y
- 7. График этой функции получается путём симметричного отображения графика y=f(x) относительно оси y. Замечание: точки пересечения графика
- 8. Примеры:
- 9. 3). График этой функции получается так: а) Если а>0 (положительное), то путем параллельного переноса графика y=f(x)
- 10. Примеры:
- 11. 4). График этой функции получается так: а) Если а>0 (положительное), то путем параллельного переноса графика y=f(x)
- 12. Примеры:
- 13. График этой функции получается так: а) Если а>1, то путём растяжения графика y=f(x) вдоль оси Oy
- 14. Примеры:
- 15. 6). График этой функции получается так: а) Если а>1, то путём сжатия графика y=f(x) вдоль оси
- 16. Примеры:
- 17. 7). График этой функции получается так: Части графика y=f(x), лежащие над осью Ox и на оси
- 18. Примеры:
- 19. 8). График этой функции получается так: На промежутке x≥0 график исходной функции y=f(x) сохраняется; На промежутке
- 20. Примеры:
- 21. y=-f(x) y=f(-x) y=f(x)+a y=f(x+a) y=a·f(x) y=f(a·x) y=|f(x)| y=f(|x|) Итог по теме
- 23. Скачать презентацию




















 Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс)
Проектная деятельность на уроках математики. Задания для групповой работы (1-2 класс) Иррациональные уравнения. 8 класс
Иррациональные уравнения. 8 класс Степени. Алгебраические выражения
Степени. Алгебраические выражения Признаки равенства треугольников
Признаки равенства треугольников Табличное умножение и деление. Решение задач изученных видов. 3 класс
Табличное умножение и деление. Решение задач изученных видов. 3 класс Презентация на тему Математические ребусы
Презентация на тему Математические ребусы  Производная функции. Геометрический смысл производной
Производная функции. Геометрический смысл производной Презентация на тему Взаимно обратные функции
Презентация на тему Взаимно обратные функции  Dei_774_stvitelnye_chisla
Dei_774_stvitelnye_chisla Сложение и вычитание в пределах первого десятка
Сложение и вычитание в пределах первого десятка Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования
Организация работы учителя с обучающимися, испытывающими трудности в обучении математике на уровне основного общего образования Задачи на готовых чертежах (геометрия, 7 класс)
Задачи на готовых чертежах (геометрия, 7 класс) parallelogramm._svoystva_parallelogramma
parallelogramm._svoystva_parallelogramma Тест на основе шаблона Баженова А. А
Тест на основе шаблона Баженова А. А Презентация на тему Призма и ее свойства
Презентация на тему Призма и ее свойства  Теория вероятности в ЕГЭ . По математике примеры и решения
Теория вероятности в ЕГЭ . По математике примеры и решения Решение типовых задач Параллельность прямых и плоскостей
Решение типовых задач Параллельность прямых и плоскостей Круг, окружность, длина окружности. 6 класс
Круг, окружность, длина окружности. 6 класс Вписанный угол
Вписанный угол Таблицы. Алгебра 7 класс
Таблицы. Алгебра 7 класс Вычисления с многозначными числами
Вычисления с многозначными числами Презентация на тему Решение экспериментальных задач
Презентация на тему Решение экспериментальных задач  Углы между прямыми и плоскостями (координатный метод), 11 класс
Углы между прямыми и плоскостями (координатный метод), 11 класс Выборочное наблюдение. Практическое занятие
Выборочное наблюдение. Практическое занятие Интерактивный тренажёр Счет в пределах 15
Интерактивный тренажёр Счет в пределах 15 Египетский треугольник
Египетский треугольник Признаки параллельности прямых
Признаки параллельности прямых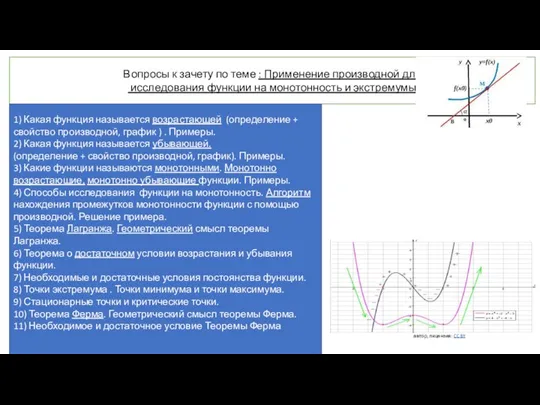 Применение производной для исследования функции на монотонность и экстремумы
Применение производной для исследования функции на монотонность и экстремумы