Содержание
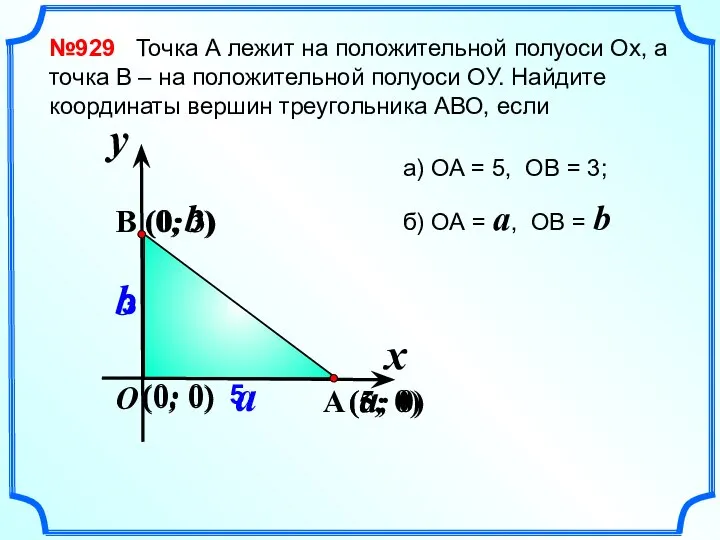
- 2. №929 Точка А лежит на положительной полуоси Ох, а точка В – на положительной полуоси ОУ.
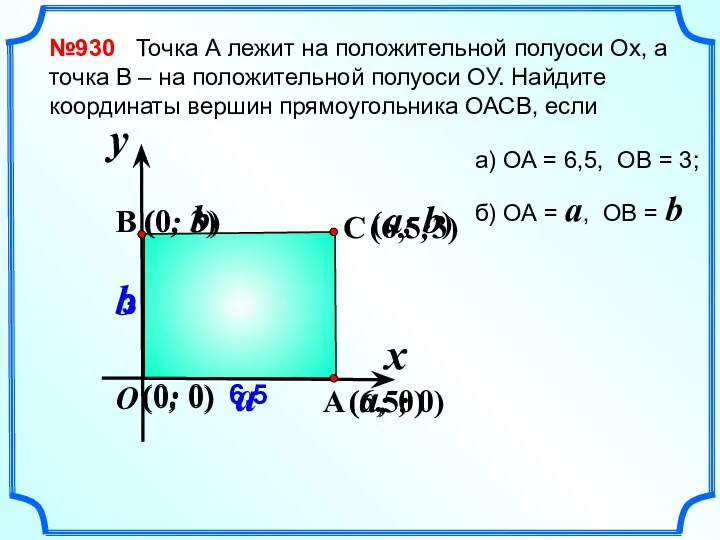
- 3. (6,5;3) (a; 0) №930 Точка А лежит на положительной полуоси Ох, а точка В – на
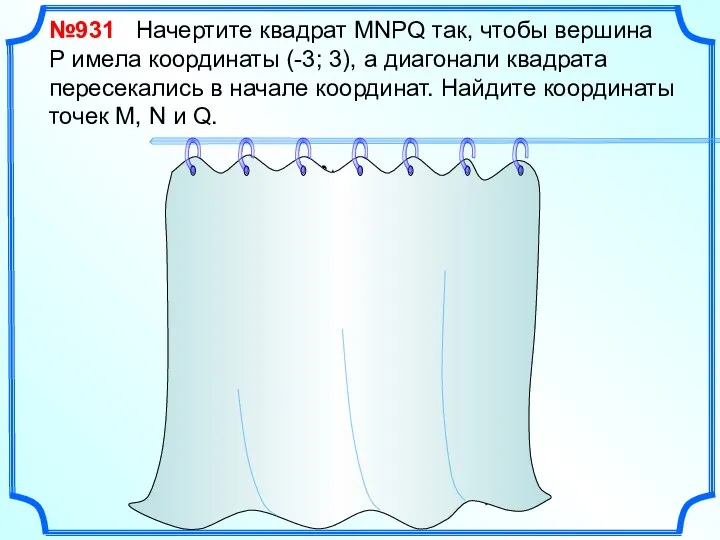
- 4. №931 Начертите квадрат MNPQ так, чтобы вершина Р имела координаты (-3; 3), а диагонали квадрата пересекались
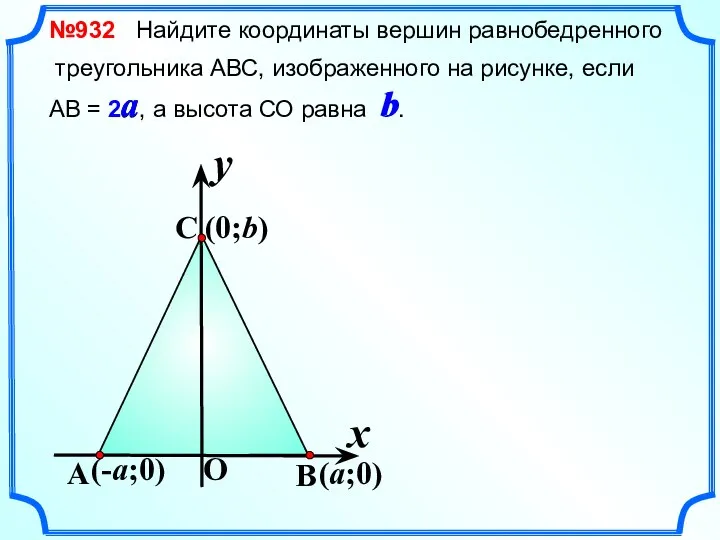
- 5. №932 Найдите координаты вершин равнобедренного треугольника АВС, изображенного на рисунке, если АВ = 2a, а высота
- 6. №933 Найдите координаты вершины D параллелограмма АВСD, если А(0; 0), В(5; 0), С(12; -3). x y
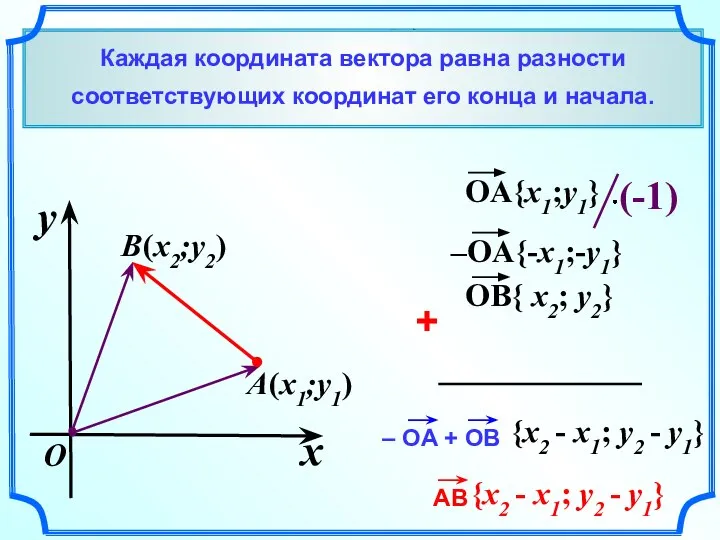
- 7. Каждая координата вектора равна разности соответствующих координат его конца и начала. x y O (x1;y1) (x2;y2)
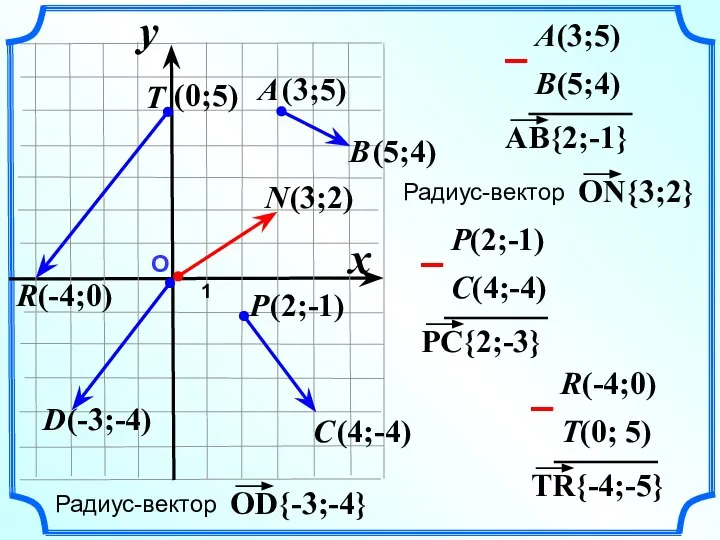
- 8. О 1 x y B(5;4) A(3;5) C(4;-4) P(2;-1) T(0; 5) R(-4;0)
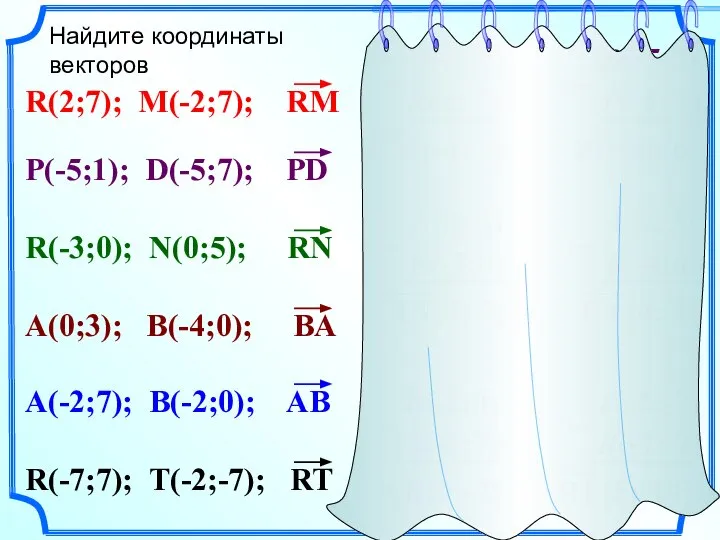
- 9. Найдите координаты векторов R(2; 7) M(-2;7) P(-5; 1) D(-5;7) R(-3;0) N(0; 5) B(-4;0) A(0; 3) A(-2;7)
- 10. { } Найти координаты векторов. Вводите ответы в текстовые поля, не делая пробелов { } {
- 11. B(5; 4) A(x; y) 5 – x = 2 x = 3 4 – y =
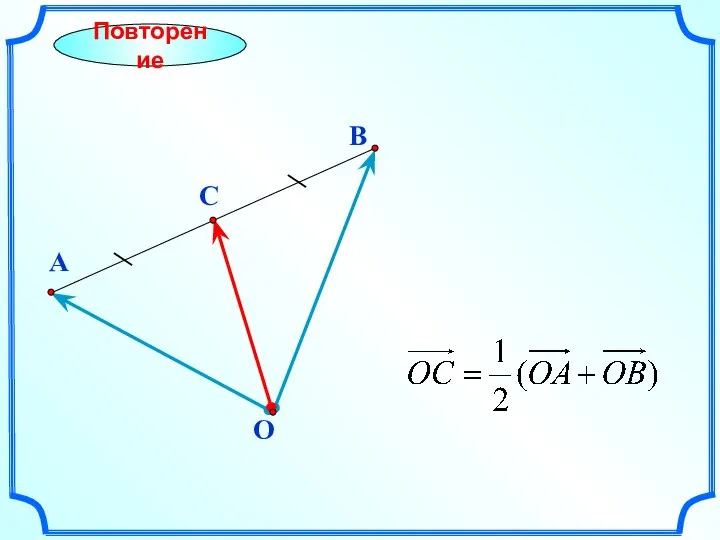
- 12. B Повторение A
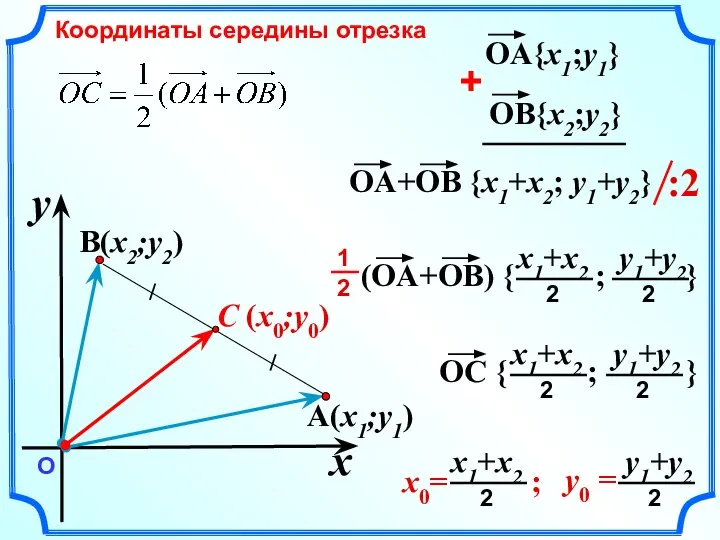
- 13. C (x0;y0) A(x1;y1) B(x2;y2) x y О Координаты середины отрезка
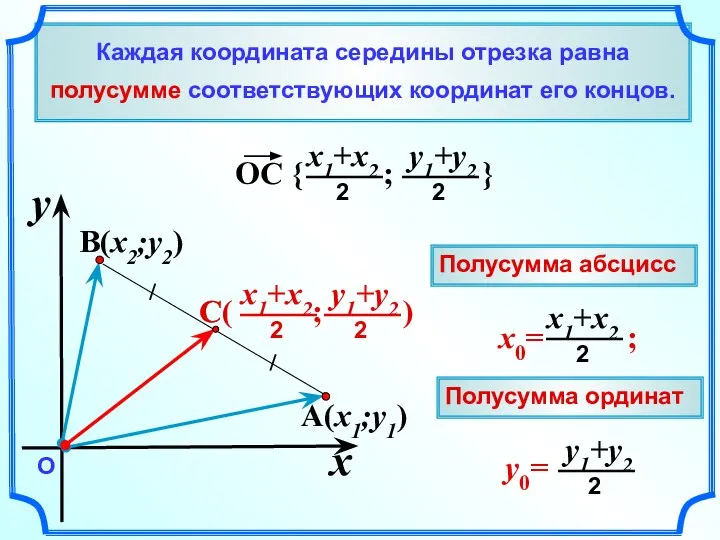
- 14. Каждая координата середины отрезка равна полусумме соответствующих координат его концов. A(x1;y1) B(x2;y2) x y О Полусумма
- 15. О 1 x y A (3;5) B(5;4) Полусумма абсцисс Полусумма ординат
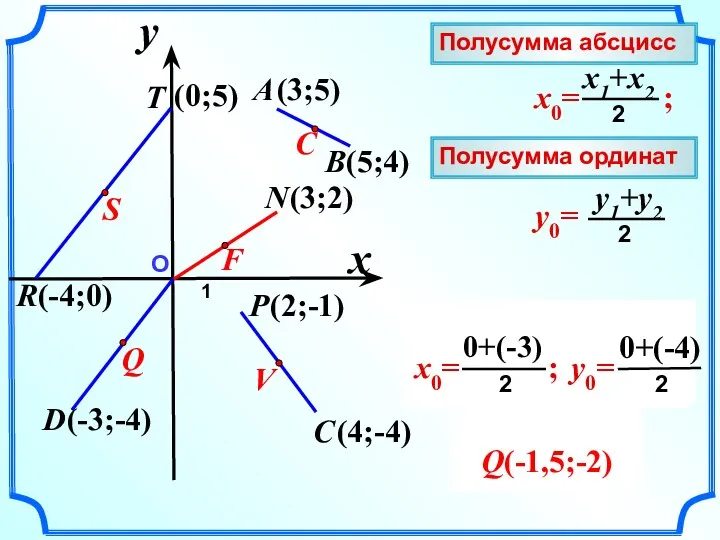
- 16. Найдите координаты cередин отрезков R(2;7); M(-2;7); C P(-5;1); D(-5;7); C R(-3;0); N(0;5); C A(0;-6); B(-4;2); C
- 17. ( ) ( ) ( ) ( ) ( ) ( ) Найти координаты середин отрезков.
- 18. Дано: Найти: A(5; 4); C(-3; 2) – середина отрезка AB B(x; y) Обратная задача. – 6
- 19. = = x y О Вычисление длины вектора по его координатам OA2=OA12 + AA12 OA2= x2
- 20. Расстояние между двумя точками M2(x2;y2) M1(x1;y1) d
- 21. № 940 Найдите расстояние между точками A(2;7) и B(-2;7) 1 способ 2 способ B(-2; 7) A(
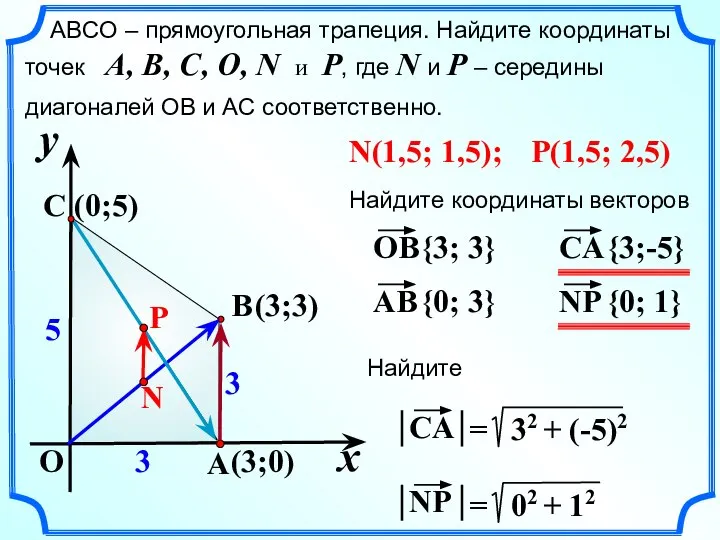
- 22. x y O A C B 5 3 3 ABCО – прямоугольная трапеция. Найдите координаты точек
- 24. Скачать презентацию









 Элементы теории фредгольмовых отображений
Элементы теории фредгольмовых отображений Геометрия в искусстве
Геометрия в искусстве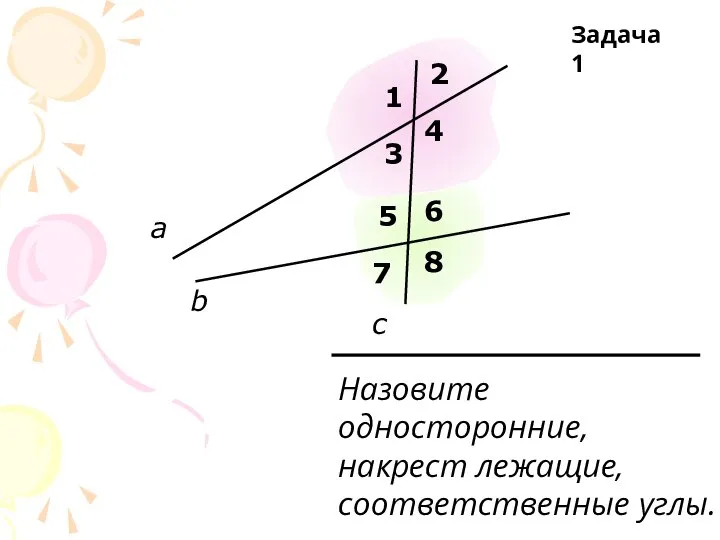 55 задач по теме параллельность
55 задач по теме параллельность Тела вращения. Цилиндр
Тела вращения. Цилиндр Действия с десятичными дробями 5 класс
Действия с десятичными дробями 5 класс Уравнение tg x =a
Уравнение tg x =a Предел последовательности. Бесконечно убывающая геометрическая прогрессия
Предел последовательности. Бесконечно убывающая геометрическая прогрессия Симметрия, как она есть
Симметрия, как она есть Своя игра. Треугольники
Своя игра. Треугольники Презентация на тему Приведение дробей к общему знаменателю
Презентация на тему Приведение дробей к общему знаменателю  Презентация на тему Длина и меры ее измерения
Презентация на тему Длина и меры ее измерения  Генеральная средняя
Генеральная средняя Экспресс-подготовка к ЗНО по математике
Экспресс-подготовка к ЗНО по математике Векторы в пространстве
Векторы в пространстве Презентация на тему Урок по теме «Координатная плоскость» 6 класс
Презентация на тему Урок по теме «Координатная плоскость» 6 класс  Решение задач по теме Параллелограмм
Решение задач по теме Параллелограмм Первый признак равенства треугольников
Первый признак равенства треугольников Организация экспериментов с использованием системных принципов
Организация экспериментов с использованием системных принципов Развёртка, как основа объёмной конструкции
Развёртка, как основа объёмной конструкции Алгоритмы решения простейших тригонометрических неравенств
Алгоритмы решения простейших тригонометрических неравенств Геометрические фигуры (открытый урок - игра Поле чудес)
Геометрические фигуры (открытый урок - игра Поле чудес) Теорема Пифагора
Теорема Пифагора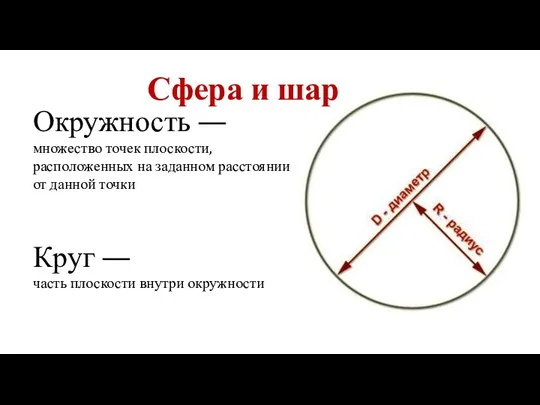 Сфера и шар
Сфера и шар Презентация на тему Принцесса математики Софья Ковалевская
Презентация на тему Принцесса математики Софья Ковалевская  Множество и его элементы
Множество и его элементы Презентация на тему Уравнения
Презентация на тему Уравнения  Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля
Линейные однородные дифференциальные уравнения. Формула Остроградского-Лиувилля Площадь прямоугольника
Площадь прямоугольника