Старинный способ решения задач на смеси и сплавы

Задача
(Из «Арифметики» Л.Ф.Магницкого).
У некоторого человека были для продажи вина двух сортов. Первое ценою 10 гривен за ведро, второе же ─ по 6 гривен. Захотелось ему сделать из тех двух вин, взяв по части, третье вино, чтобы ему цена была по 7 гривен. Какие части надлежит из тех двух вин взять к наполнению ведра третьего вина ценою в 7 гривен?

Старинный способ решения задачи.
1) Запишем цены вин каждого
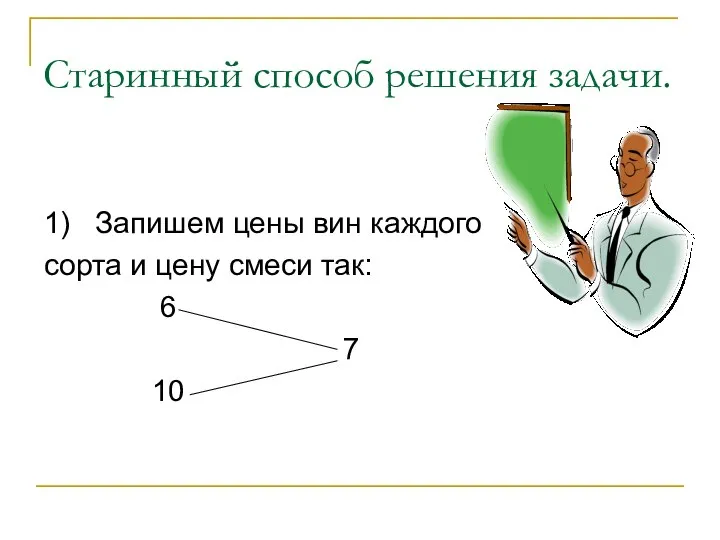
сорта и цену смеси так:
6
7
10

Старинный способ решения задачи.
2) Вычислим прибыль на
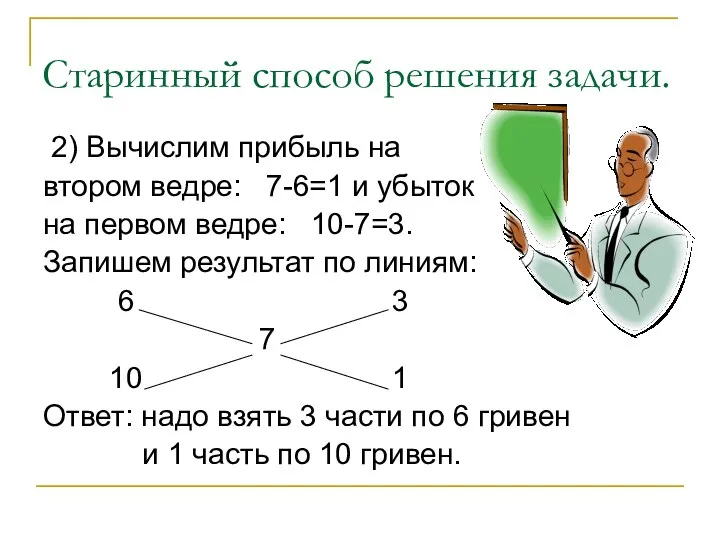
втором ведре: 7-6=1 и убыток
на первом ведре: 10-7=3.
Запишем результат по линиям:
6 3
7
10 1
Ответ: надо взять 3 части по 6 гривен
и 1 часть по 10 гривен.

Современное объяснение старинного способа решения задач.
Рассмотрим решение задачи в общем виде: Обозначим через m и M количества смешиваемых вин, а через p, P и ρ стоимости ведра вина 1 сорта, 2 сорта и смеси вин соответственно. Стоимость смеси равна сумме стоимостей смешиваемых частей:
m∙p+M∙P=(m+M)∙ρ. Получаем отношение:
m P-ρ
M ρ-p

Современное объяснение старинного
способа решения.
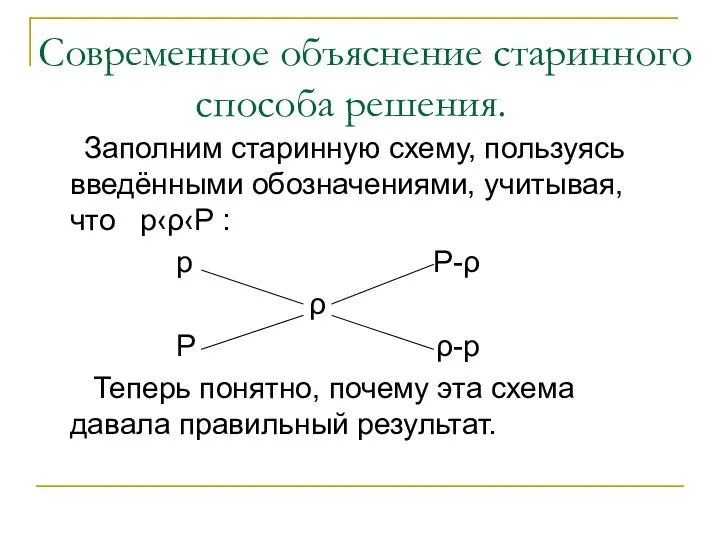
Заполним старинную схему, пользуясь введёнными обозначениями, учитывая, что p‹ρ‹P :
p P-ρ
ρ
P ρ-p
Теперь понятно, почему эта схема давала правильный результат.

Используемая в презентации литература:
«Текстовые задачи в школьном курсе математики» А.В.Шевкин, Москва Педагогический университет «Первое сентября», 2006 год.