Понятия о многогранном угле, геометрическом теле

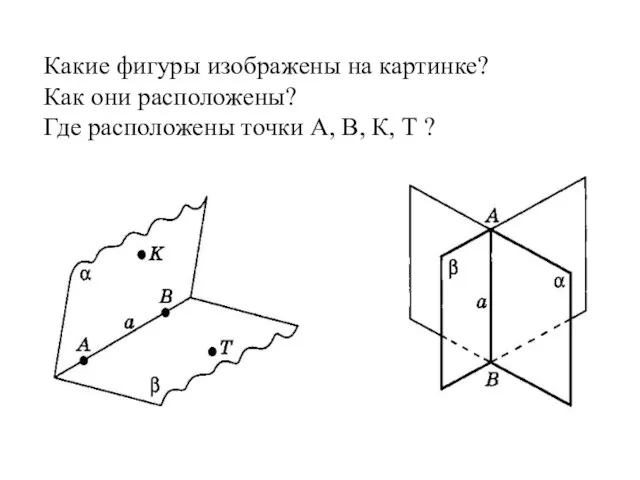
Какие фигуры изображены на картинке?
Как они расположены?
Где расположены точки А, В, К, Т ?

Составьте определение из этих ключевых слов
Прямая,
граница,
Общая,
полуплоскость

Определение
Двугранным углом называется фигура , образованная прямой а и двумя полуплоскостями с общей границей а, не принадлежащими одной плоскости . Полуплоскости, образующие двугранный угол, называются его гранями , прямая а –общая граница полуплоскостей - называется ребром двугранного угла.
Двугранный угол с гранями α, β и ребром a обозначают αаβ.

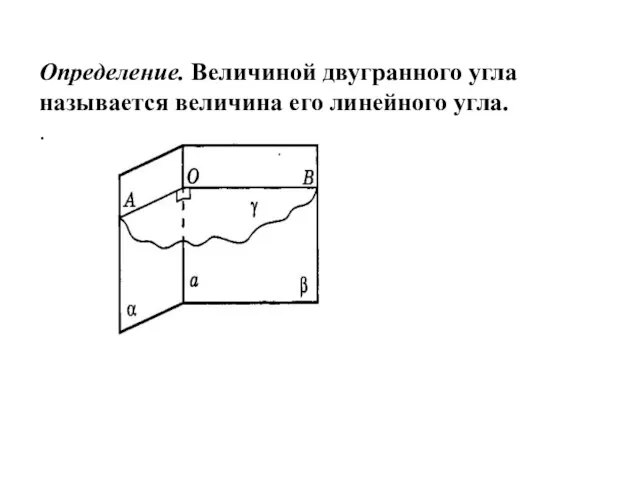
Определение. Величиной двугранного угла называется величина его линейного угла.
.

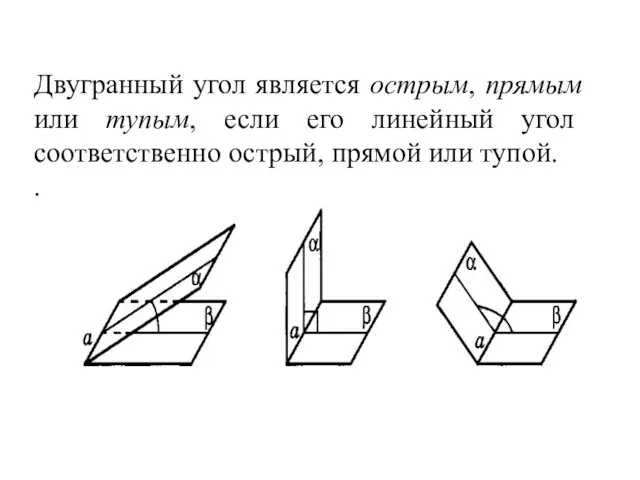
Двугранный угол является острым, прямым или тупым, если его линейный угол соответственно острый, прямой или тупой.
.

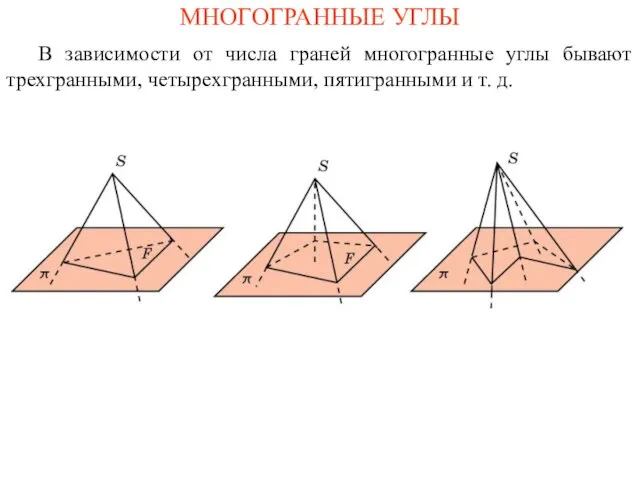
МНОГОГРАННЫЕ УГЛЫ
В зависимости от числа граней многогранные углы бывают трехгранными, четырехгранными, пятигранными и т. д.

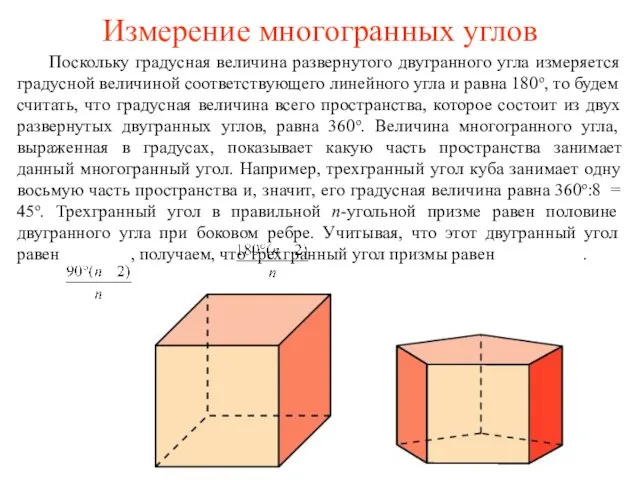
Измерение многогранных углов
Поскольку градусная величина развернутого двугранного угла измеряется градусной величиной соответствующего линейного угла и равна 180о, то будем считать, что градусная величина всего пространства, которое состоит из двух развернутых двугранных углов, равна 360о. Величина многогранного угла, выраженная в градусах, показывает какую часть пространства занимает данный многогранный угол. Например, трехгранный угол куба занимает одну восьмую часть пространства и, значит, его градусная величина равна 360о:8 = 45о. Трехгранный угол в правильной n-угольной призме равен половине двугранного угла при боковом ребре. Учитывая, что этот двугранный угол равен , получаем, что трехгранный угол призмы равен .

Упражнение 1
Может ли быть трехгранный угол с плоскими углами: а) 30°, 60°, 20°; б) 45°, 45°, 90°; в) 30°, 45°, 60°?
Ответ: а) Нет;
б) нет;
в) да.

Упражнение 2
Два плоских угла трехгранного угла равны 70° и 80°. В каких границах находится третий плоский угол?
Ответ: 10о < ϕ < 150о.

Упражнение 3
В трехгранном угле два плоских угла равны по 45°; двугранный угол между ними прямой. Найдите третий плоский угол.
Ответ: 60о.

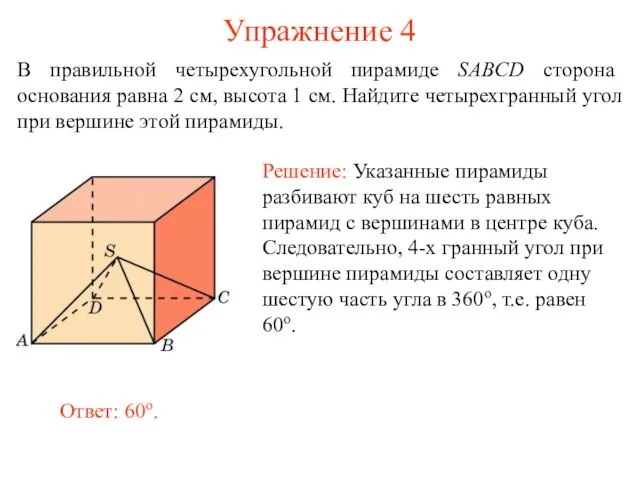
Упражнение 4
В правильной четырехугольной пирамиде SABCD сторона основания равна 2 см, высота 1 см. Найдите четырехгранный угол при вершине этой пирамиды.

ПАРАЛЛЕЛЕПИПЕД
ТЕТРАЭДР

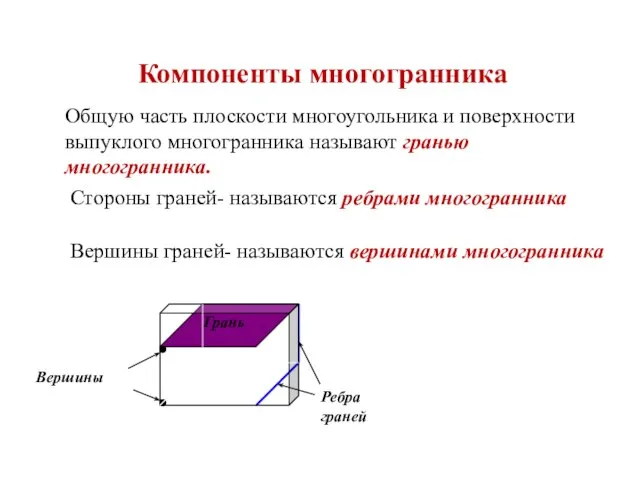
Компоненты многогранника
Общую часть плоскости многоугольника и поверхности выпуклого многогранника называют гранью многогранника.
Стороны граней- называются ребрами многогранника
Вершины граней- называются вершинами многогранника

Призма
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников.

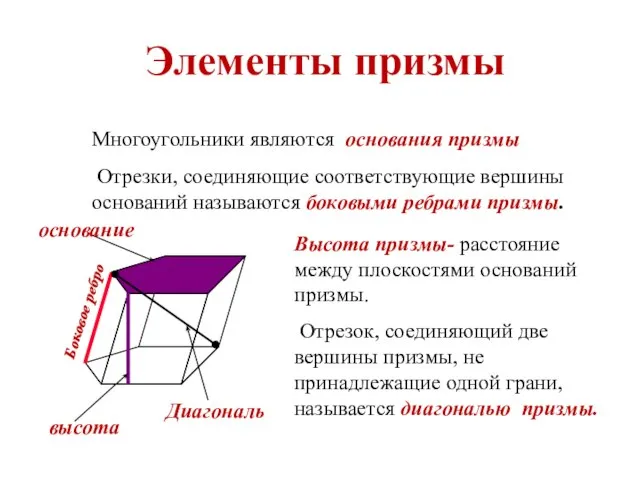
Элементы призмы
Многоугольники являются основания призмы
Отрезки, соединяющие соответствующие вершины оснований называются боковыми ребрами призмы.
Высота призмы- расстояние между плоскостями оснований призмы.
Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани, называется диагональю призмы.

Основные свойства призмы:
основания лежат в параллельных плоскостях
боковые ребра параллельны и равны
основания равны

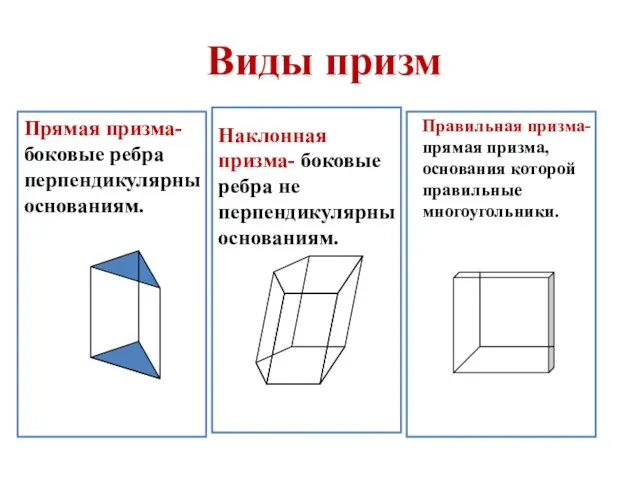
Виды призм
Прямая призма- боковые ребра перпендикулярны основаниям.
Наклонная призма- боковые ребра не перпендикулярны основаниям.
Правильная призма- прямая призма, основания которой правильные многоугольники.

Свойства параллелепипеда :
У параллелепипеда противолежащие грани параллельны и равны.
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Точка пересечения диагоналей параллелепипеда является его центром симметрии.

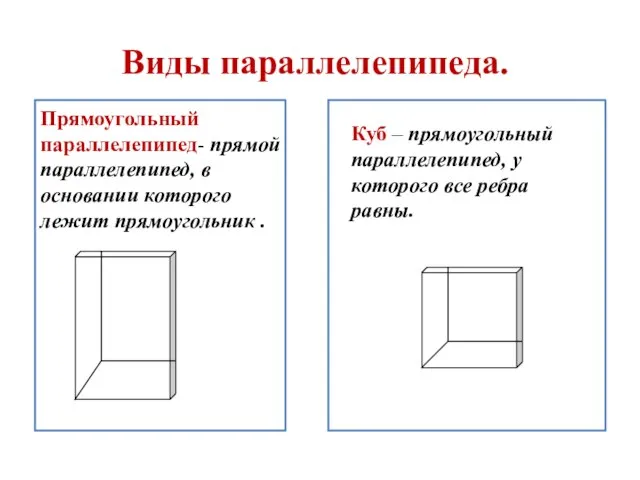
Виды параллелепипеда.
Прямоугольный параллелепипед- прямой параллелепипед, в основании которого лежит прямоугольник .
Куб – прямоугольный параллелепипед, у которого все ребра равны.

Пирамида
Пирамидой называется многогранник, который состоит из ОСНОВАНИЯ пирамиды (плоского многоугольника), ВЕРШИНЫ пирамиды и всех отрезков, соединяющих их.

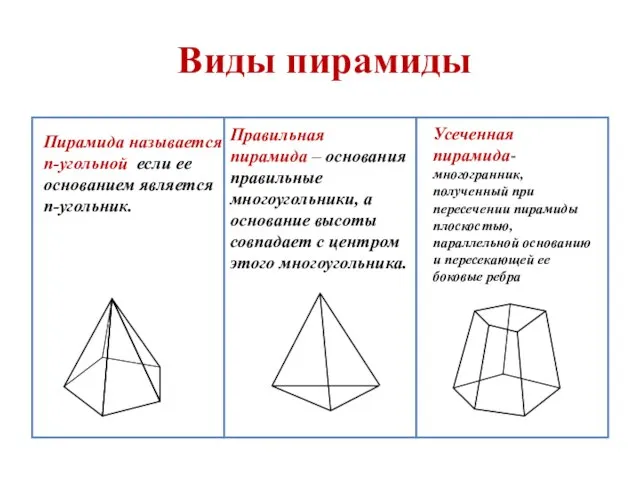
Виды пирамиды
Пирамида называется п-угольной если ее основанием является n-угольник.
Правильная пирамида – основания правильные многоугольники, а основание высоты совпадает с центром этого многоугольника.
Усеченная пирамида- многогранник, полученный при пересечении пирамиды плоскостью, параллельной основанию и пересекающей ее боковые ребра

Дворец мира и согласия — здание пирамидальной формы, созданное архитектором сэром Норманом Фостером в Нур-Султане, столице Казахстана, специально для проведения «Конгресса лидеров мировых и традиционных религий». Она заключает в себе пропорции золотого сечения: грани основания имеют длину 62 метра, и высота равна 62 метрам. Площадь боковой поверхности пирамиды равна(15376 м2)

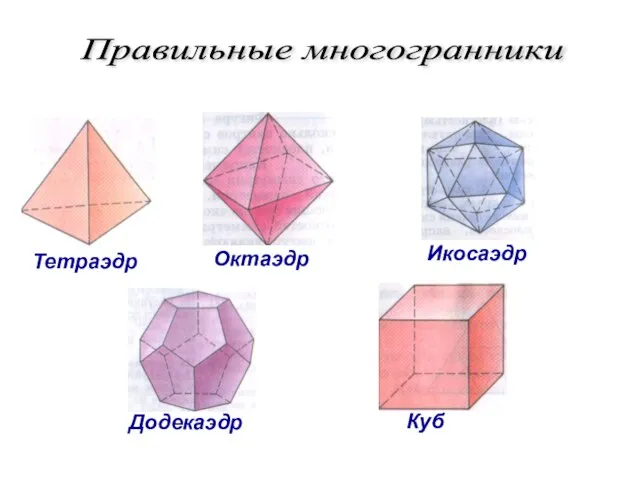
Правильные многогранники

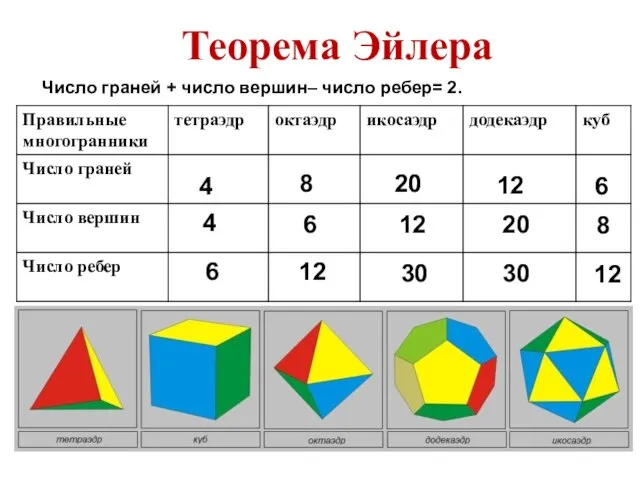
Теорема Эйлера
Число граней + число вершин– число ребер= 2.
4
4
6
8
6
12
20
12
30
12
20
30
6
8
12

Теорема Эйлера:
Теорема Эйлера для призм:
(В + Г – Р) = 2
Ребра: 3n
Вершины: 2n
Грани: n + 2
Диагонали: n·(n – 3)
Теорема Эйлера для пирамид:
(В + Г – Р) = 2
Ребра: 2n
Вершины: n + 1
Грани: n + 1
Выпуклый многогранник

№1.
В данном геометрическом теле три ребра обозначьте как а, b, c,
а) покажите, что диагональ вычисляется по формуле:
б) Вычислите диагонали геометрического тела.
с) если а=3см, b=5см и см, найдите значение с.

№2. Высота прямоугольного параллелепипеда равна 8 см, а стороны основания равны – 5см и 6 см. Найдите площадь сечения, проходящего через меньшую сторону нижнего основания и противолежащую ей сторону верхнего основания.
Дано: ABCDA1B1C1D1 – прямой параллелепипед;
АВ = 5 см; ВС = 6 см; А1А = 8 см
Найти: SАВC1D1.

3.В прямой треугольной призме стороны основания равны – 10 см, 17см и 21 см, а высота призмы равна 18 см. Найдите площадь сечения, проходящего через боковое ребро и меньшую высоту основания.

Решение задач
Решение:
Ответ: 8 см