Содержание
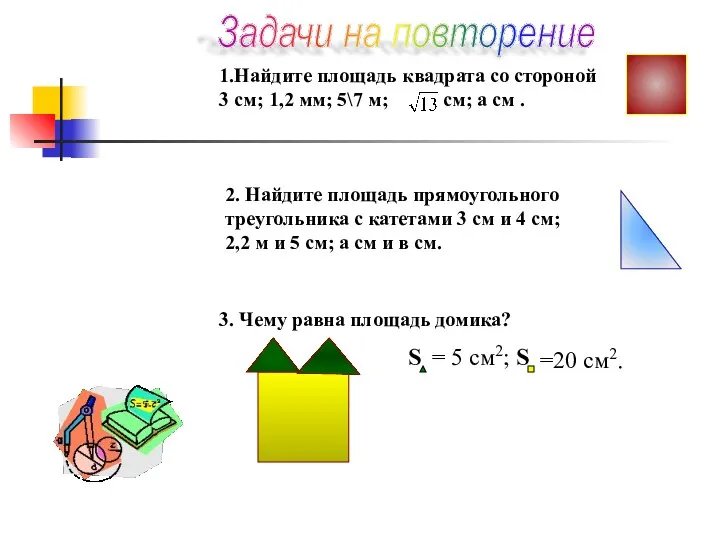
- 2. 1.Найдите площадь квадрата со стороной 3 см; 1,2 мм; 5\7 м; см; а см . 2.
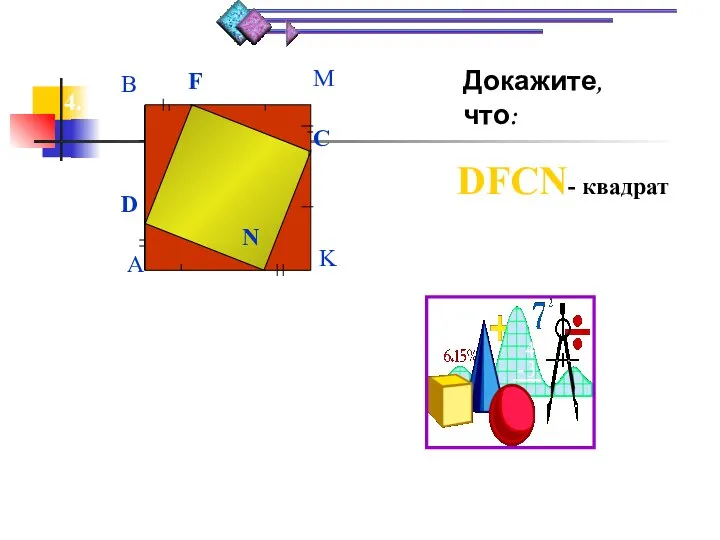
- 3. Докажите,что: DFCN- квадрат 4. D F C N A B M K
- 4. «Геометрия обладает двумя великими сокровищами.Первое – это теорема Пифагора…» О Пифагоре сохранились десятки легенд и мифов,
- 5. Знаменитый древнегреческий философ и математик Пифагор Самосский родился на острове Самос, далеко от Греции в 580
- 6. Здесь в Кретоне, рождается школа Пифагора. В пифагорейской школе занимались изучением чисел и их свойств, много
- 8. a b c a b c a b c a b c В прямоугольном треугольнике квадрат
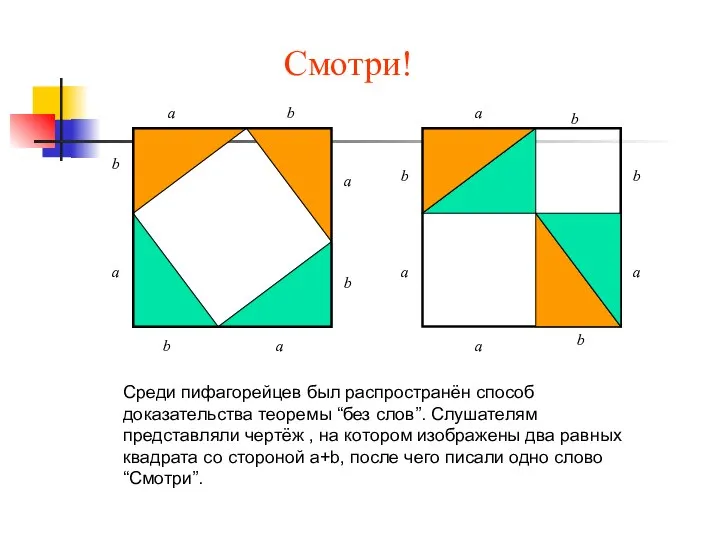
- 9. a a a a a a a a b b b b b b b b
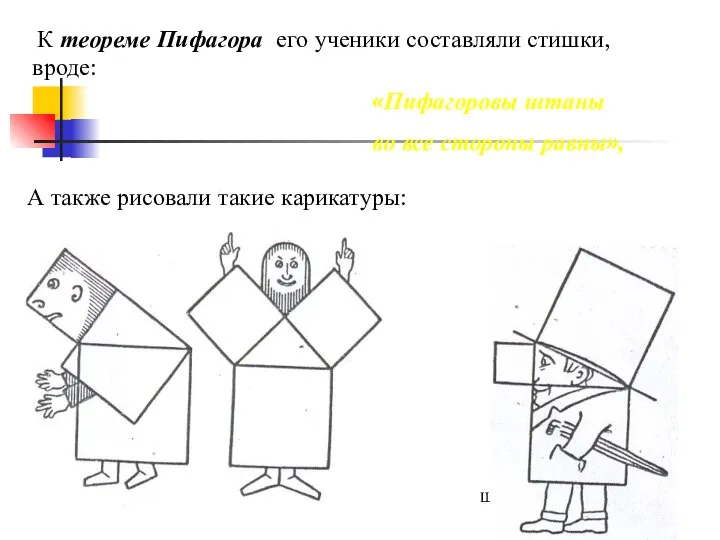
- 10. К теореме Пифагора его ученики составляли стишки, вроде: «Пифагоровы штаны во все стороны равны», А также
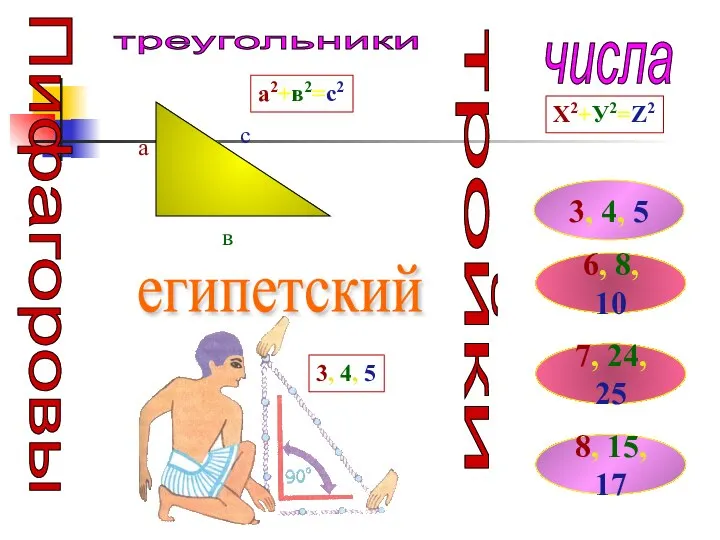
- 12. Пифагоровы тройки числа треугольники Х2+У2=Z2 3, 4, 5 6, 8, 10 7, 24, 25 8, 15,
- 13. С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые
- 16. Скачать презентацию








 История метрологии и теории измерений
История метрологии и теории измерений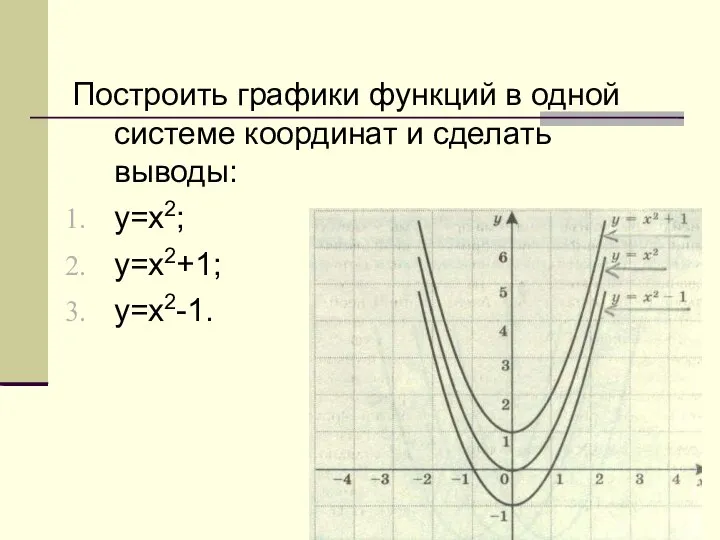 Преобразования графика квадратичной функции. Преобразования графика
Преобразования графика квадратичной функции. Преобразования графика برای رسم یک خط به دو نقطه نیاز داریم وخط از دو طرف ادامه دارد
برای رسم یک خط به دو نقطه نیاز داریم وخط از دو طرف ادامه دارد Simple Affirmative Negative Speaking
Simple Affirmative Negative Speaking Блок-схемы алгоритмов
Блок-схемы алгоритмов Свойства тригонометрических функций
Свойства тригонометрических функций Вынесение общего множителя за скобки. 6 класс
Вынесение общего множителя за скобки. 6 класс Логарифмические функции
Логарифмические функции Методы многокритериальной оптимизации
Методы многокритериальной оптимизации Использование Microsoft Exel в проектных работах по математике
Использование Microsoft Exel в проектных работах по математике Треугольник. Задачи по готовым чертежам (7 класс)
Треугольник. Задачи по готовым чертежам (7 класс) Квадратики 3-5
Квадратики 3-5 Производная обратной функции
Производная обратной функции Математическая карусель
Математическая карусель Викторина О, счастливчик (шуточные тесты математика вокруг нас)
Викторина О, счастливчик (шуточные тесты математика вокруг нас) Физико-математические основы ОФЭКТ
Физико-математические основы ОФЭКТ Статистическая обработка вариационного ряда
Статистическая обработка вариационного ряда Логика, делимость. Задание №15
Логика, делимость. Задание №15 Операции реляционной алгебры
Операции реляционной алгебры Параллельность прямых и плоскостей в пространстве
Параллельность прямых и плоскостей в пространстве Переменные. Арифметические операции
Переменные. Арифметические операции Презентация на тему Алгебра и начала математического анализа
Презентация на тему Алгебра и начала математического анализа  Дополнительные построения в трапеции при решении задач
Дополнительные построения в трапеции при решении задач Объем куба. Задача
Объем куба. Задача Презентация на тему Первообразная 11 класс
Презентация на тему Первообразная 11 класс  Свойство вертикальных углов
Свойство вертикальных углов Решение уравнения cosx=a
Решение уравнения cosx=a Алгоритмы направленного перебора
Алгоритмы направленного перебора