Декартова система координат

Две перпендикулярные прямые, на каждой из которых выбрано положительное направление и задан единичный отрезок, образуют прямоугольную систему координат на плоскости.
Эти две прямые называются осями координат, а точка их пересечения началом координат.
Прямоугольная система координат на плоскости

Плоскость, на которой задана прямоугольная система координат, называют координатной плоскостью. Оси образуют четыре прямых угла — это координатные углы или координатные четверти (иногда называют квадрантами). Их нумеруют, как показано на рисунке .
Координатная плоскость

Рене Декарт (1596-1650) - французский философ, математик, механик, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики, автор метода радикального сомнения в философии, механицизма в физике, предтеча рефлексологии.
Декартова система координат
Прямоугольную систему координат на плоскости придумал в 1637 году французский математик Рене Декарт, поэтому у неё есть второе название: «Декартова система координат».

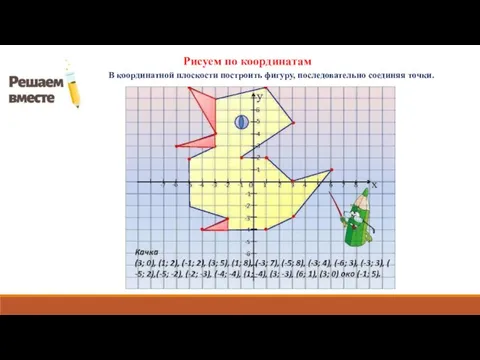
Каждой точке плоскости можно сопоставить пару чисел — её координаты. Чтобы это сделать, надо провести через точку две прямые, параллельные осям координат. Координаты точек пересечения этих прямых с осями координат будут координатами данной точки.
Координаты точки
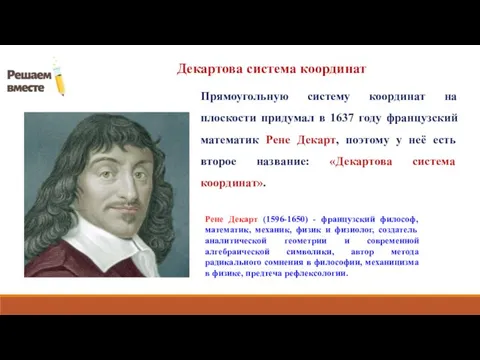
В целом координаты точки в декартовой системе координат на плоскости принято обозначать парой чисел в круглых скобках. Первой всегда записывают координату по оси х, эту координату называют абсциссой точки. Второй записывают координату по оси у, её называют ординатой точки.
а – абсцисса точки (значение по оси х)
b – ордината точки (значение по оси у)

Если точка лежит на оси абсцисс, то её ордината равна нулю, и наоборот: если точка лежит на оси ординат, то её абсцисса равна нулю.
Координаты точки
Точка на оси абсцисс Р(3;0)
Точка на оси ординат Q (0;-2)
Начало координат О(0;0).

Определите координаты точек

Определите, какая точка имеет координаты (-3; -3)?

Определите, какая точка имеет координаты (-1; 1)?

Определите, какая точка имеет координаты (3; 4)?

Определите, какая точка имеет координаты (0; 3)?

Рисуем по координатам
В координатной плоскости построить фигуру, последовательно соединяя точки.