Слайд 3Показатели СМО
Среднее количество требований, которые СМО обслуживает за единицу времени,
Средний процент требований,

которые не были обслужены,
Вероятность того, что пришедшее в систему требование будет принято на обслуживание,
Среднее время ожидания требования в очереди,
Закон распределения времени ожидания,
Среднее количество требований в очереди,
Закон распределения числа требований в очереди,
Коэффициент загрузки прибора обслуживания,
Среднее количество приборов занятых обслуживанием.
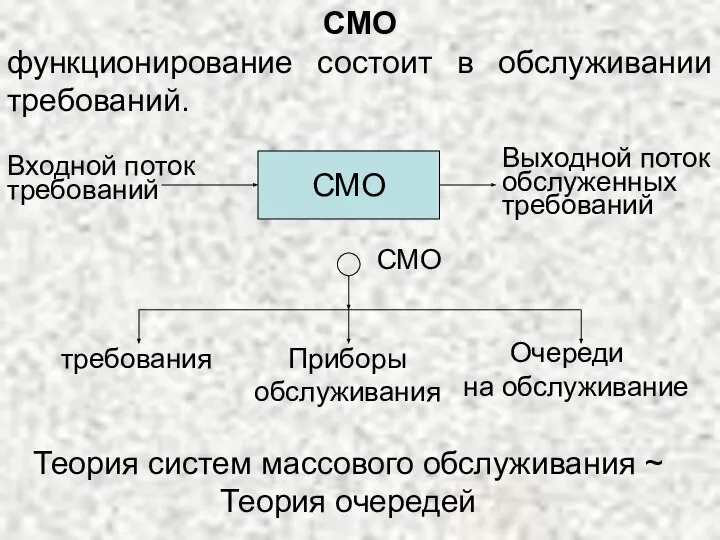
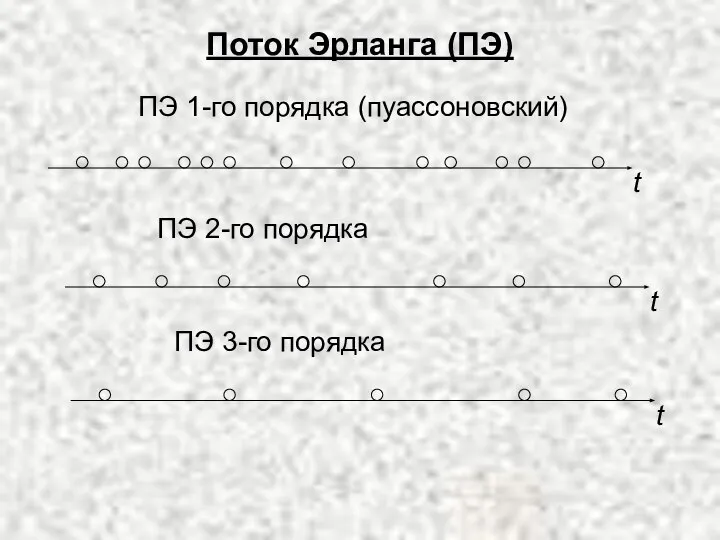
Слайд 5Входной поток требований
Пуассоновский (простейший) поток

Слайд 7Стационарность: вероятность прихода определенного
количества требований за время t зависит только от
длины
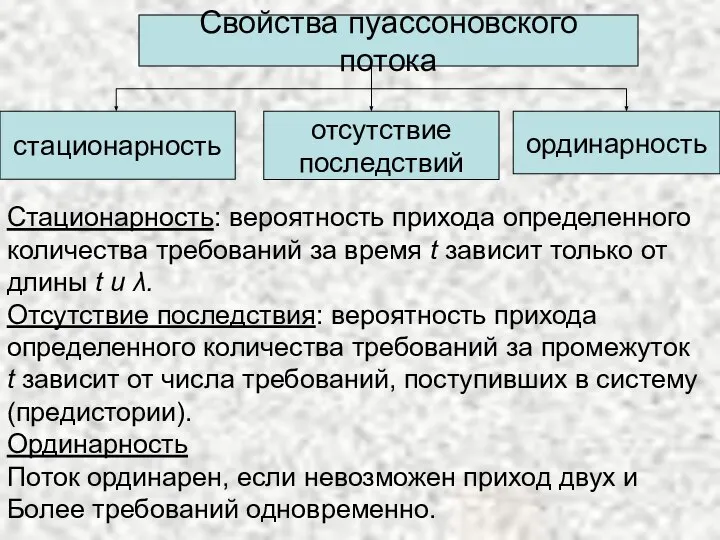
t и λ.
Отсутствие последствия: вероятность прихода
определенного количества требований за промежуток
t зависит от числа требований, поступивших в систему
(предистории).
Ординарность
Поток ординарен, если невозможен приход двух и
Более требований одновременно.
Слайд 12Типы моделей СМО
X/Y/Z
где X - распределение времени прибытия требований,
Y -

распределение времени обслуживания,
Z - количество приборов.
Например,
M/M/1 G/G/m
D/D/1 M/G/1
где М - марковский процесс,
D - дискретный процесс,
G - произвольное распределение.
Слайд 13Закон сохранения стационарной очереди
(формула Литтла)
0
2
4
6
8
10
12
количество
требований
N(t)
случайный процесс прихода требований за промежуток

(0, t),
выходной поток требований из системы на промежутке
(0, t),
общая «работа» (произведение количества требований
на время их пребывания в СМО за промежуток (0, t)),


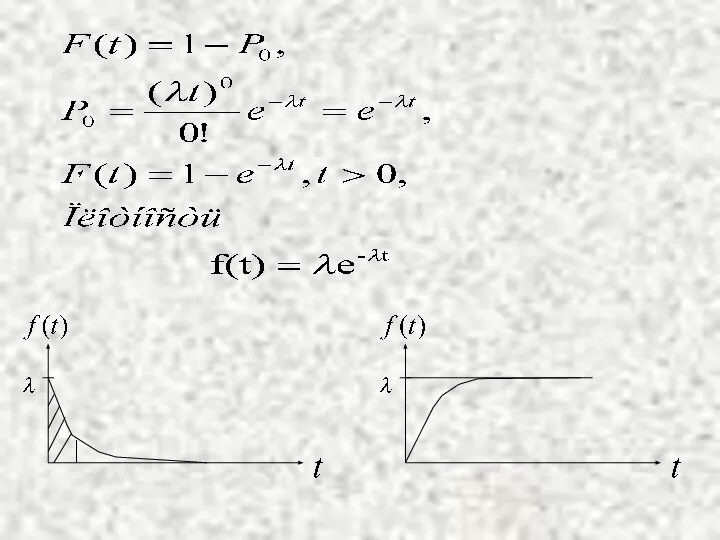



 Векторы в пространстве
Векторы в пространстве Математический диктант к уроку по теме Параллелограмм
Математический диктант к уроку по теме Параллелограмм Презентация на тему Дробные числа
Презентация на тему Дробные числа  Геометрические преобразования плоскости
Геометрические преобразования плоскости Сумма углов треугольника
Сумма углов треугольника Построение графика квадратичной функции
Построение графика квадратичной функции Приведите примеры элементарных исследований свойств при изучении первых функций
Приведите примеры элементарных исследований свойств при изучении первых функций Буйство красок, звуков, рифм смиряет циркуль, логарифм
Буйство красок, звуков, рифм смиряет циркуль, логарифм Презентация на тему Цилиндр: основные сведения
Презентация на тему Цилиндр: основные сведения  Линейное уравнение с двумя переменными
Линейное уравнение с двумя переменными Правило сложения, вычитания, умножения десятичных дробей
Правило сложения, вычитания, умножения десятичных дробей Сложение чисел. Как можно найти значение суммы 7 + 7
Сложение чисел. Как можно найти значение суммы 7 + 7 Урок сюрприз. Величины
Урок сюрприз. Величины Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг)
Пространственные векторы в асинхронном двигателе. Эйлер (1707-1783 гг) Осевая симметрия
Осевая симметрия Решение задач на перебор вариантов
Решение задач на перебор вариантов Формулы сокращенного умножения. Интерактивный плакат
Формулы сокращенного умножения. Интерактивный плакат Правильные многогранники и ИДСЗ
Правильные многогранники и ИДСЗ Число Пи вокруг нас
Число Пи вокруг нас Закрепление таблицы умножения и деления
Закрепление таблицы умножения и деления Соответствия между множествами. Отображения. Функции
Соответствия между множествами. Отображения. Функции Божьи коровки
Божьи коровки Методы решения тригонометрических уравнений
Методы решения тригонометрических уравнений Решение линейных уравнений. Часть 2
Решение линейных уравнений. Часть 2 Математический диктант. Классная работа
Математический диктант. Классная работа Многоугольники
Многоугольники Степень с натуральным показателем
Степень с натуральным показателем