Слайд 2Цель и задачи
Цель работы: Ознакомиться с темой непрерывные дроби.
Задачи: исследовать свойства цепных

дробей и возможные действия, производимые с ними
Слайд 3Непрерывные дроби
Последовательность, каждый член которой является обычной дробью, порождает непрерывную (или цепную)

дробь, если ее второй член прибавить к первому, а каждую дробь, начиная с третьей, прибавить к знаменателю предыдущей дроби. Например, последовательность 1, 1/2, 2/3, 3/4, ..., n/(n + 1), ... порождает непрерывную дробь
где многоточие в конце указывает на то, что процесс продолжается бесконечно. В свою очередь непрерывная дробь порождает другую последовательность дробей, называемых подходящими.
Слайд 4Представление рациональных чисел непрерывными дробями.
Целое число, являющееся делителем каждого из целых чисел

, называется общим делителем этих чисел. Общий делитель этих чисел называется их наибольшим общим делителем, если он делится на всякий общий делитель данных чисел.
Слайд 5Подходящие дроби
Задаче разложения обыкновенной дроби в непрерывную дробь противостоит обратная задача –

обращения или свертывания цепной дроби в простую дробь При этом основную роль играют дроби вида:
Которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа




 Интерактивный тренажёр Счет в пределах 15
Интерактивный тренажёр Счет в пределах 15 Математические методы в филологии
Математические методы в филологии Построение сечения
Построение сечения Окружность и её элементы
Окружность и её элементы Универсальный тренажёр. Математика 2 класс
Универсальный тренажёр. Математика 2 класс Презентация на тему Круговые диаграммы (6 класс)
Презентация на тему Круговые диаграммы (6 класс)  Числовые домики. Тренажер
Числовые домики. Тренажер Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт
Задачи на готовых чертежах. Первый признак равенства треугольников. Устный счёт Вычисление неопределенного интеграла
Вычисление неопределенного интеграла Логические задачи. Мастер-класс
Логические задачи. Мастер-класс Метрологические аспекты спектрометрических и радиометрических измерений
Метрологические аспекты спектрометрических и радиометрических измерений Вопросы при решении задач
Вопросы при решении задач Функция y = k/х и её график
Функция y = k/х и её график Алгоритм нахождения интервалов выпуклости и точек перегиба
Алгоритм нахождения интервалов выпуклости и точек перегиба Векторы в пространстве. Задачи
Векторы в пространстве. Задачи Решение тригонометрических уравнений. 10 класс
Решение тригонометрических уравнений. 10 класс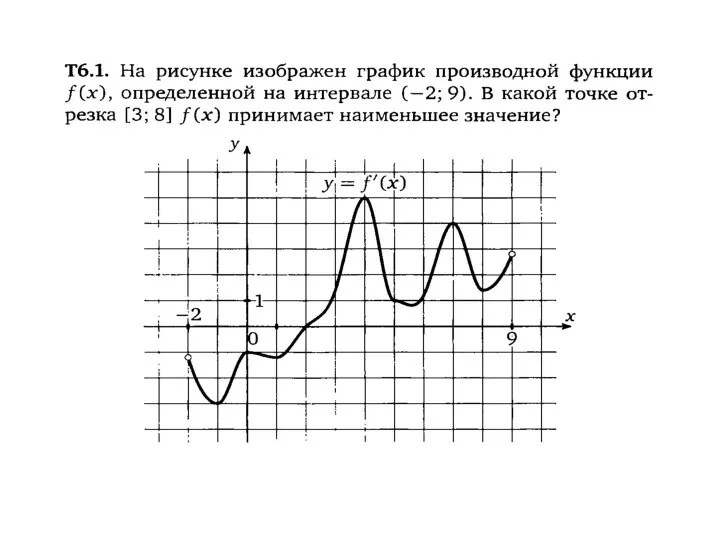 График производной функции
График производной функции Решение задач на работу
Решение задач на работу Письменное умножение и деление
Письменное умножение и деление Реляционная алгебра
Реляционная алгебра Комплeксные числа. Арифметические операции над ними (10 класс)
Комплeксные числа. Арифметические операции над ними (10 класс) Повторение. Дроби
Повторение. Дроби Прямо-пропорциональные величины
Прямо-пропорциональные величины Числовая последовательность
Числовая последовательность Решение неравеснств
Решение неравеснств Решение задач на движение. 8 класс
Решение задач на движение. 8 класс Lek-AFK-Differentsialnye_uravnenia
Lek-AFK-Differentsialnye_uravnenia Линейная функция. Блиц-опрос
Линейная функция. Блиц-опрос