Дискретное преобразование Фурье (окончание)

Тема 6. Дискретное преобразование Фурье (продолжение)
Тема 6. Дискретное преобразование Фурье
6. Дискретное преобразование Фурье
6.1. Общие сведения
6.2. Свойства дискретного преобразования Фурье
6.3. Быстрое преобразование Фурье
6.4. Связь дискретного преобразования Фурье и дискретной фильтрации
6.5. Алгоритм Герцеля
6.6. Дискретная фильтрация с помощью быстрого преобразования Фурье

6.5. Алгоритм Герцеля
Алгоритм БПФ очень эффективен, но он осуществляет вычисление всех отсчетов спектра, следовательно, этот алгоритм нельзя приспособить для вычисления только какого-то небольшого набора отсчетов спектра. В тех случаях, когда нужно определить не все гармоники, а только их ограниченный набор, может оказаться выгоднее пользоваться обычным дискретным преобразованием Фурье (ДПФ).
Напомним, что ДПФ задается формулой
Напомним также, что в предыдущем подразделе "Связь дискретного преобразования Фурье и дискретной фильтрации" было показано, что формально вычисление отсчета спектра сигнала можно свести к вычислению выхода некоторой гипотетической дискретной системой с импульсной характеристикой hn[k],

Алгоритм Герцеля
а именно,
и импульсной передаточной функцией Wn(z)
В литературе сказано, что членом z-N можно пренебречь, Действительно, пусть обрабатывается серия из N отсчетов сигнала. Когда серия закончится, все обнулится и вычисление начинается сначала. Слагаемое в числителе z-N учитывает, что когда будет обрабатываться последний отсчет, из него будет вычитаться первый отсчет серии. Поэтому это слагаемое можно не учитывать. В этом случае мы получаем рекурсивный фильтр первого порядка в виде

Алгоритм Герцеля
Коэффициент обратной связи в фильтре получился комплексным. Для каждого отсчета надо выполнить четыре вещественных умножения и столько же вещественных сложений. Число операций можно сократить. Для этого преобразуем приведенное выше выражение
Теперь рекурсивная часть имеет вещественные коэффициенты, в которой надо выполнить одно вещественное умножение и два вещественных сложения. В рекурсивной части фильтра комплексные коэффициенты исчезли, но они появились в числителе, то есть в нерекурсивной части фильтра.

Алгоритм Герцеля
Если реализовать фильтр в канонической форме (см. рис. ниже)
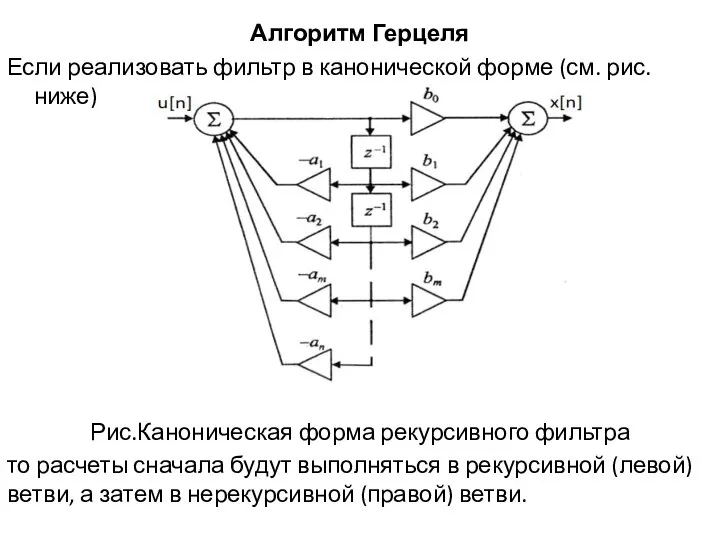
Рис.Каноническая форма рекурсивного фильтра
то расчеты сначала будут выполняться в рекурсивной (левой) ветви, а затем в нерекурсивной (правой) ветви.

Алгоритм Герцеля
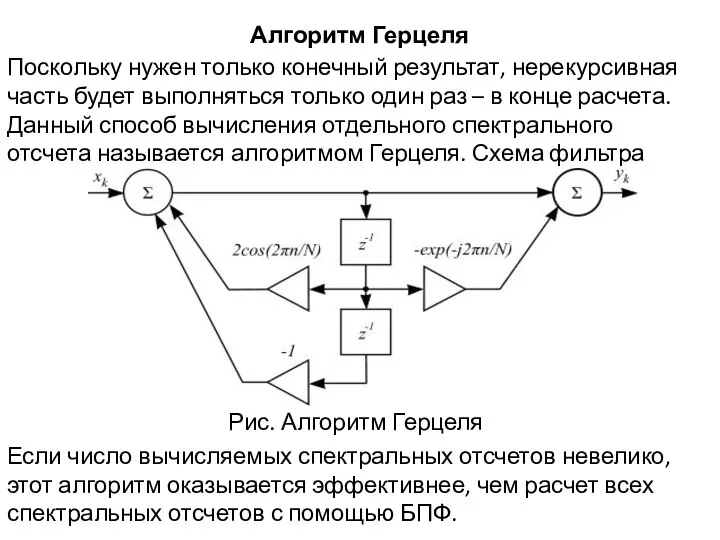
Поскольку нужен только конечный результат, нерекурсивная часть будет выполняться только один раз – в конце расчета. Данный способ вычисления отдельного спектрального отсчета называется алгоритмом Герцеля. Схема фильтра
Рис. Алгоритм Герцеля
Если число вычисляемых спектральных отсчетов невелико, этот алгоритм оказывается эффективнее, чем расчет всех спектральных отсчетов с помощью БПФ.

6.6. Дискретная фильтрация с помощью БПФ
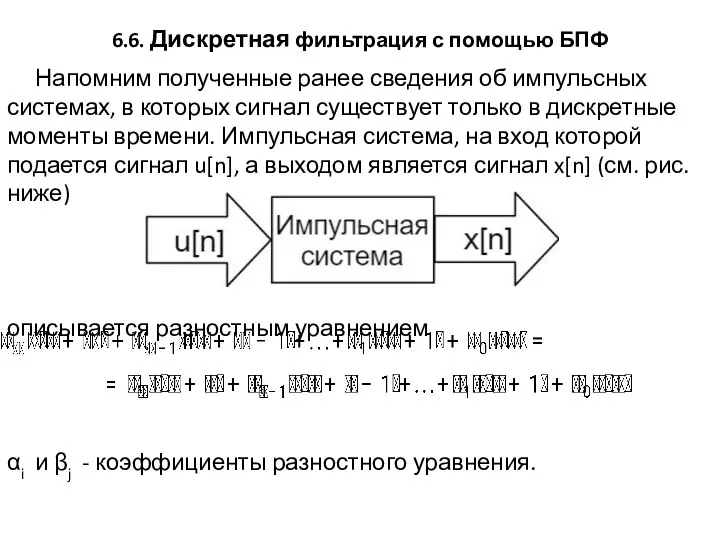
Напомним полученные ранее сведения об импульсных системах, в которых сигнал существует только в дискретные моменты времени. Импульсная система, на вход которой подается сигнал u[n], а выходом является сигнал x[n] (см. рис. ниже)
описывается разностным уравнением
αi и βj - коэффициенты разностного уравнения.

Дискретная фильтрация с помощью БПФ
Разностное уравнение связывает значения входа и выхода системы в дискретные моменты времени и позволяет организовать рекуррентный процесс вычисления выходных дискретных значений.
В более удобном способе описания импульсной системы используются Z-преобразование U(z) входного сигнала u[n]
Z-преобразование X(z) выходного сигнала x[n]
и импульсная передаточная функция, которая вводится как отношение Z -преобразования выхода X(z) к Z -преобразованию входа U(z),

Дискретная фильтрация с помощью БПФ
а именно,
Связь между Z -преобразованиями входа и выхода задается выражением
Связь между импульсной передаточной функцией W*(z) передаточной функцией по Фурье (частотной передаточной функцией) W*(jω) импульсной системы задается с помощью подстановки z =ejωτ (τ-шаг дискретизации)

Дискретная фильтрация с помощью БПФ
Следовательно, связь между преобразованием Фурье (спектр) входа U*(jω)
и преобразованием Фурье (спектр) выхода X*(jω)
задается выражением

Дискретная фильтрация с помощью БПФ
Важное замечание
Обратим внимание, что при вычислении преобразований Фурье дискретных сигналов u[n] и x[n] учитывается тот факт, что эти сигналы являются непериодическими дискретными сигналами. Следовательно, преобразования Фурье (спектры) U*(jω) и X*(jω) этих дискретных непериодических сигналов являются непрерывными функциями частоты ω.
Конец замечания.
Еще в одном способе описания импульсной системы используется импульсная характеристика h[n]. По определению, импульсная характеристика h[n] – это переходной процесс импульсной системы при действии цифрового единичного импульса

Дискретная фильтрация с помощью БПФ
Ранее было показано, что импульсная передаточная функция является Z-преобразованием импульсной характеристики h[n]
Следовательно, импульсная характеристика h[n] является обратным Z-преобразованием от импульсной передаточной функции W*(z)
Ранее также было показано, что выходной сигнал x[n] импульсной системы с импульсной характеристикой h[n] с числом отсчетов N2 и входным сигналом u[n] с числом отсчетов N1 вычисляется по формуле линейной свертки
L - длина результата линейной свертки, равная
L= N1 + N2 – 1.

Дискретная фильтрация с помощью БПФ
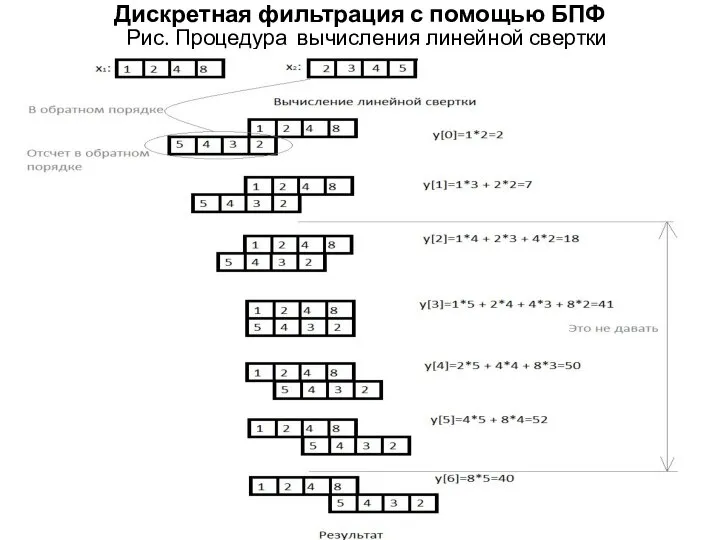
На рис. ниже приведем иллюстративный численный пример вычисления выходного сигнала x[n] импульсной системы с импульсной характеристикой h[n] с числом отсчетов N2 = 4 при входном сигнале u[n] с числом отсчетов N1 = 4 по формуле линейной свертки, где
u[n] = x1[n] = 1, 2, 4, 8
h[n] = x2[n] = 2, 3, 4, 5
x[n] = y [n]

Дискретная фильтрация с помощью БПФ
Рис. Процедура вычисления линейной свертки

Дискретная фильтрация с помощью БПФ
Видим, что число отсчетов L выходного сигнала x[n], вычисленного по формуле линейной свертки равно
L= N1 + N2 – 1 = 4+4-1=7.
Теперь давайте попробуем решить задачу дискретной фильтрации с использованием дискретного преобразования Фурье (ДПФ), а значит предполагая, что входной сигнал u[n] , импульсная характеристика h[n], выходной сигнал x[n] являются периодическими последовательностями.
В этом случае можно поступить, например следующим образом:
- используя ДПФ в форме быстрого преобразования Фурье (БПФ), вычислим спектр U[n] входного дискретного сигнала u[n] с числом отсчетов N1;
- используя ДПФ в форме быстрого преобразования Фурье (БПФ), вычислим спектр (частотную передаточную функцию) W[n] импульсной характеристики h[n] с числом отсчетов N2;

Дискретная фильтрация с помощью БПФ
вычислим спектр [n] выходного дискретного сигнала x[n] как произведение частотной передаточной функции W[n] системы и спектра U[n] входного дискретного сигнала u[n]
Перемножение мы можем осуществить только при выполнении очевидного условия: число отсчетов у частотной передаточной функции W[n] и у спектра U[n] входного дискретного сигнала u[n] должно быть одинаковым, т.е N1 = N2 = N, а значит число отсчетов у импульсной характеристики h[n] и у входного дискретного сигнала u[n] должно быть одинаковым и равным N;
- используя обратное ДПФ в форме обратного быстрого преобразования Фурье (БПФ), получим версию выходного дискретного сигнала x[n] с числом отсчетов N.

Дискретная фильтрация с помощью БПФ
Мы получили неверный результат, поскольку у правильной версии выходного дискретного сигнала x[n] , вычисленной ранее по формуле линейной свертки
число отсчетов должно быть равно N = N - 1= 2N - 1
Ошибка заключается в том, что используя при решении задачи дискретной фильтрации с использованием дискретного преобразования Фурье (ДПФ), мы получили результат круговой свертки, а не линейной свертки, поскольку при использовании ДПФ предполагается , что входной сигнал u[n] , импульсная характеристика h[n], выходной сигнал x[n] являются периодическими последовательностями.
Напомним, что круговая свертка последовательностей h[n] и u[n], как периодических, вычисляется по формуле

Дискретная фильтрация с помощью БПФ
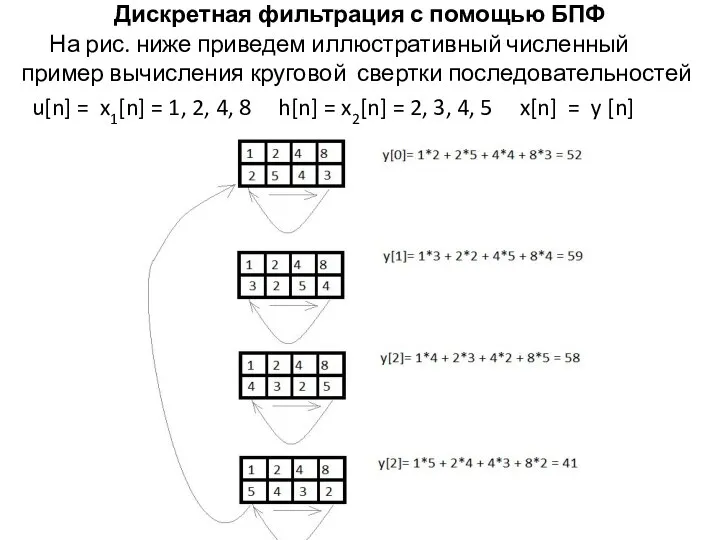
На рис. ниже приведем иллюстративный численный пример вычисления круговой свертки последовательностей
u[n] = x1[n] = 1, 2, 4, 8 h[n] = x2[n] = 2, 3, 4, 5 x[n] = y [n]

Дискретная фильтрация с помощью БПФ
Видно, что результаты линейной и круговой сверток разные. Чтобы сделать результат круговой свертки равным результату линейной свертки надо в круговой свертке исходные последовательности h[n] и u[n] дополнить нулями так, чтобы схема круговой свертки была подобна схеме линейной свертки. Определим, каким числом нулей надо дополнить исходные последовательности h[n] и u[n].
Мы знаем, что длина результата линейной свертки равна
L= N1 + N2 – 1,
где N1 и N2 -длины последовательностей u[n] и h[n].
Значит длина результата круговой свертки также должна быть равна L. Но эта длина равна количеству тактов в круговой свертке. А значит и количество тактов должно быть также равно L.

Дискретная фильтрация с помощью БПФ
Следовательно, длина каждой из последовательностей u[n] и h[n], фигурирующих в круговой свертке, должна быть равна L, т.е. дополнена нулями до длины L. На рисунке ниже показан результат вычисления круговой свертки дополненных нулями последовательностей u[n] и h[n]
u[n] = x1[n] = 1, 2, 4, 8
h[n] = x2[n] = 2, 3, 4, 5
x[n] = y [n]

Дискретная фильтрация с помощью БПФ
Процедура круговой свертки модифицир-ных последовательностей

Дискретная фильтрация с помощью БПФ
Видно, что действительно совпадают результаты процедур на рис. Процедура линейной свертки и на рис. Процедура круговой свертки модифицированных последовательностей.
Теперь опишем процесс дискретной фильтрация с помощью ДПФ в форме БПФ для определения выхода дискретной системы в виде следующей последовательности (используемые обозначения приведены на рис. ниже):
Рис. Используемые обозначения входного и выходного сигналов и импульсной характеристики.

Дискретная фильтрация с помощью БПФ
1. Исходные последовательности отсчетов входного сигнала и импульсной характеристики дополняются нулями так, чтобы их длины стали одинаковыми и равными сумме длин исходных последовательностей без единицы.
2. Вычисляются по отдельности с помощью БПФ спектры дополненных нулями входного сигнала и импульсной характеристики (т.е. вычисляем спектры U[n] и W[n]соответственно).
3. Спектры U[n] и W[n] перемножаются (это означает, что перемножаются спектр входа и передаточная функция). Следовательно, в силу соотношения
X[n]= W[n]U[n]
мы получаем спектр выхода.
4. Вычисляем обратное ДПФ в форме обратного БПФ от результата перемножения (мы получаем выход системы, который, с другой стороны, равен линейной свертке исходных последовательностей).

Дискретная фильтрация с помощью БПФ
Приведем набор команд пакета MATLAB, позволяющий сравнить работу функции линейной свертки conv и приведенного алгоритма.
>>u=[1,2,3,4]; % Набор отсчетов входного сигнала
>>h=[2,3,4,5]; %Набор отсчетов импульсной характеристики
>>x1=conv(u,h) % Печать отсчетов выходного сигнала
>>U=fft(u,8); % Спектр входного сигнала, дополненного нулями
% до восьми позиций
>>W=fft(h,8); % Частотная передаточная функция - спектр
% импульсной характеристики, дополненной нулями
% до восьми позиций
>>X=W*U; % Спектр выходного сигнала
>>x2=ifft(X) % Печать отсчетов выходного сигнала.
% Проверьте x1=x2

Дискретная фильтрация с помощью БПФ
Число нулей, добавляемых в последовательности, может быть больше необходимого. Это только добавит нули в конец результата. Тогда можно сделать длины входных последовательностей кратными степени двойки и применить алгоритм БПФ. Это существенно сократит число операций.
Недостаток описанного метода заключается в том, что входной сигнал обрабатывается целиком. Поэтому надо ждать окончания поступления информации и возникают задержки в обработке. Обычно требуют обрабатывать информацию по мере её поступления.
Возможным решением проблемы является блочная обработка входного сигнала. Входная последовательность делится на блоки желательно с длиной, равной степени двойки. Чем меньше будут блоки, тем меньше будет запаздывание в обработке. Чем больше блок, тем больше запаздывание в обработке, но тем эффективнее будет выгода от алгоритма БПФ.

Дискретная фильтрация с помощью БПФ
Блоки обрабатываются по отдельности. Результат обработки блока присоединяется к предыдущему результату со следующей поправкой.
Пусть N - длина блока,
M - длина импульсной характеристики.
В конце результата обработки каждого блока находится «хвост» переходного процесса после «выключения» входного сигнала. Длина «хвоста» M-1 позиция (длина реакции импульсной характеристики на последний отсчет входного сигнала). Общая длина результата обработки блока N+M-1. Но в начале каждого блока имеет место переходный процесс, так как процесс обработки блока не учитывает отсчеты предыдущего блока, и мы имеем как бы нулевые начальные условия. Длина этого переходного процесса M-1 отсчет. Однако информация об отсчетах предыдущего блока находится в «хвосте» предыдущего блока. Таким образом, получается, что результаты обработки блоков не просто присоединяются друг другу. Они перекрываются.

Дискретная фильтрация с помощью БПФ
.
Начало длиною M-1 отсчетов результата обработки очередного блока перекрывается и суммируется с концом результата предыдущего блока такой же длины.
Пример. Постоянные отсчеты подаются на дискретный эквивалент апериодического звена. При обработке очередного блока мы получим в начале процесса возрастающую экспоненту 1-e-αt, потом будет установившееся постоянное значение. После конца блока мы получим «хвост» - убывающую экспоненту e-αt , которую надо прибавить к началу обработки следующего блока. Сумма двух экспонент: возрастающей и убывающей равна константе – установившемуся значению, что и требуется