Дисперсионный анализ

Назначение метода
Дисперсионный анализ – анализ изменчивости признака под влиянием каких-либо контролируемых переменных факторов.
Методами дисперсионного анализа устанавливается наличие влияния заданного фактора на изучаемый процесс (на выходную переменную процесса) за счёт статистической обработки наблюдаемой совокупности выборочных данных.

Назначение метода
Дисперсионный анализ есть совокупность статистических методов, предназначенных для проверки гипотез о связи между определенными признаками и исследуемыми факторами, которые не имеют количественного описания, а также для установления степени влияния факторов и их взаимодействия. В специальной литературе его часто называют ANOVA (от англоязычного названия Analysis of Variations). Впервые этот метод был разработан Р. Фишером в 1925 г.

Типы решаемых задач
Основной целью дисперсионного анализа является исследование значимости различия между средними. Установить различаются ли три группы или более по какому-либо одному количественному признаку
Обобщенно задача дисперсионного анализа состоит в том, чтобы из общей вариативности признака выделить три частные вариативности:
- Вариативность, обусловленную действием каждой из исследуемых независимых переменных.
- Вариативность, обусловленную взаимодействием исследуемых независмых переменных.
- Вариативность случайную, обусловленную всеми неучтенными обстоятельствами.

Цель и задачи
Цель: выявить дифференциацию представлений о нормативном сексуальном поведении среди представителей различных поколений в современной России и определяющие её факторы.
Задачи:
1. Проанализировать теоретико-методологические подходы к проблеме сексуальной нормы в научной литературе.
2. Обобщить результаты эмпирических исследований о дифференциации представлений о сексуальной норме среди населения современной России.
3. Определить факторы, обусловливающие различия в представлениях о сексуальной норме среди населения России в целом
4. Выявить специфику межпоколенных различий в представлениях о сексуальной норме в Архангельской области по сравнению с общероссийской ситуацией

Возможности применения методов в социологических исследования
Применительно к социологическим данным таковыми являются частости различных вариантов ответов респондентов на вопросы анкет массовых опросов, измеряемые в процентах от общего числа ответов и интерпретируемые как вероятности отношения изучаемых групп населения к исследуемым социальным явлениям или процессам.

Этапы
Построение дисперсионного комплекса.
Вычисление средних квадратов отклонений.
Вычисление дисперсии
Сравнение факторной и остаточной дисперсий
Оценка результатов с помощью теоретических значений распределения Фишера-Снедекор

Методы (методики, разновидности) данного вида анализа
Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок, которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По количеству выявляемых регулируемых факторов дисперсионный анализ может быть однофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие).

Суть метода, формулы
Однофакторный дисперсионный анализ основан на том, что сумму квадратов отклонений статистического комплекса возможно разделить на компоненты:
SS = SSa + SSe,
Где:
SS - общая сумма квадратов отклонений,
SSa - объяснённая влиянием фактора a сумма квадратов отклонений,
SSe - необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки.

Если через ni обозначить число вариантов в каждом классе градации (группе) и a - общее число градаций фактора (групп), то - общее число наблюдений и можно получить следующие формулы:
общее число квадратов отклонений:
объяснённая влиянием фактора a сумма квадратов отклонений:
необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки:
Где
- общее среднее наблюдений,
- среднее наблюдений в каждой градации фактора (группе).

Кроме того,
где - дисперсия градации фактора (группы).

Чтобы провести однофакторный дисперсионный анализ данных статистического комплекса, нужно найти фактическое отношение Фишера - отношение дисперсии, объяснённой влиянием фактора (межрупповой), и необъяснённой дисперсии (внутригрупповой):
и сравнить его с критическим значением Фишера:

Дисперсии рассчитываются следующим образом:
- объяснённая дисперсия,
- необъяснённая дисперсия,
при этом
va = a − 1 - число степеней свободы объяснённой дисперсии,
ve = n − a - число степеней свободы необъяснённой дисперсии,
v = n − 1 - общее число степеней свободы.

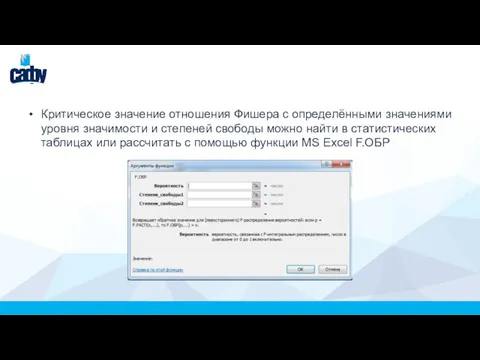
Критическое значение отношения Фишера с определёнными значениями уровня значимости и степеней свободы можно найти в статистических таблицах или рассчитать с помощью функции MS Excel F.ОБР

Двухфакторный анализ
Двухфакторный дисперсионный анализ применяется для того, чтобы проверить возможную зависимость результативного признака от двух факторов - A и B. Тогда a - число градаций фактора A и b - число градаций фактора B. В статистическом комплексе сумма квадратов остатков разделяется на три компоненты:
SS = SSa + SSb + SSe,
- общая сумма квадратов отклонений,
- объяснённая влиянием фактора A сумма квадратов отклонений,
-объяснённая влиянием фактора B сумма квадратов отклонений,

- необъяснённая сумма квадратов отклонений или сумма квадратов отклонений ошибки,
- общее среднее наблюдений,
- среднее наблюдений в каждой градации фактора A,
- среднее число наблюдений в каждой градации фактора B.
Дисперсии вычисляются следующим образом:
- дисперсия, объяснённая влиянием фактора A,
- дисперсия, объяснённая влиянием фактора B,
- необъяснённая дисперсия или дисперсия ошибки,

Где:
va = a − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора A,
vb = b − 1 - число степеней свободы дисперсии, объяснённой влиянием фактора B,
ve = (a − 1)(b − 1) - число степеней свободы необъяснённой дисперсии или дисперсии ошибки,
v = ab − 1 - общее число степеней свободы.
Если факторы не зависят друг от друга, то для определения существенности факторов выдвигаются две нулевые гипотезы и соответствующие альтернативные гипотезы:
для фактора A:
H0: μ1A = μ2A = ... = μaA,
H1: не все μiA равны;
для фактора B:
H0: μ1B = μ2B = ... = μaB,
H1: не все μiB равны.

Если фактическое отношение Фишера больше критического отношения Фишера, то следует отклонить нулевую гипотезу с уровнем значимости α. Это означает, что фактор существенно влияет на данные: данные зависят от фактора с вероятностью P = 1 − α.
Если фактическое отношение Фишера меньше критического отношения Фишера, то следует принять нулевую гипотезу с уровнем значимости α. Это означает, что фактор не оказывает существенного влияния на данные с вероятностью P = 1 − α.